Logical reasoning
| ||||||||||||||||||||||||||||||||||||||||||||||||
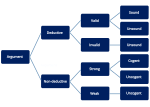
| Logical reasoning is concerned with the correctness of arguments. A key distinction is between deductive and non-deductive arguments. |
Logical reasoning is a mental activity that aims to arrive at a conclusion in a rigorous way. It happens in the form of inferences or arguments by starting from a set of premises and reasoning to a conclusion supported by these premises. The premises and the conclusion are propositions, i.e. true or false claims about what is the case. Together, they form an argument. Logical reasoning is norm-governed in the sense that it aims to formulate correct arguments that any rational person would find convincing. The main discipline studying logical reasoning is logic.
Distinct types of logical reasoning differ from each other concerning the norms they employ and the certainty of the conclusion they arrive at. Deductive reasoning offers the strongest support: the premises ensure the conclusion, meaning that it is impossible for the conclusion to be false if all the premises are true. Such an argument is called a valid argument, for example: all men are mortal; Socrates is a man; therefore, Socrates is mortal. For valid arguments, it is not important whether the premises are actually true but only that, if they were true, the conclusion could not be false. Valid arguments follow a rule of inference, such as modus ponens or modus tollens. Deductive reasoning plays a central role in formal logic and mathematics.
For non-deductive logical reasoning, the premises make their conclusion rationally convincing without ensuring its truth. This is often understood in terms of probability: the premises make it more likely that the conclusion is true and strong inferences make it very likely. Some uncertainty remains because the conclusion introduces new information not already found in the premises. Non-deductive reasoning plays a central role in everyday life and in most sciences. Often-discussed types are inductive, abductive, and analogical reasoning. Inductive reasoning is a form of generalization that infers a universal law from a pattern found in many individual cases. It can be used to conclude that "all ravens are black" based on many individual observations of black ravens. Abductive reasoning, also known as "inference to the best explanation", starts from an observation and reasons to the fact explaining this observation. An example is a doctor who examines the symptoms of their patient to make a diagnosis of the underlying cause. Analogical reasoning compares two similar systems. It observes that one of them has a feature and concludes that the other one also has this feature.
Arguments that fall short of the standards of logical reasoning are called fallacies. For formal fallacies, like affirming the consequent, the error lies in the logical form of the argument. For informal fallacies, like false dilemmas, the source of the faulty reasoning is usually found in the content or the context of the argument. Some theorists understand logical reasoning in a wide sense that is roughly equivalent to critical thinking. In this regard, it encompasses cognitive skills besides the ability to draw conclusions from premises. Examples are skills to generate and evaluate reasons and to assess the reliability of information. Further factors are to seek new information, to avoid inconsistencies, and to consider the advantages and disadvantages of different courses of action before making a decision.
Definition[edit]
Logical reasoning is a form of thinking that is concerned with arriving at a conclusion in a rigorous way.[1] This happens in the form of inferences by transforming the information present in a set of premises to reach a conclusion.[2][3] It can be defined as "selecting and interpreting information from a given context, making connections, and verifying and drawing conclusions based on provided and interpreted information and the associated rules and processes."[4] Logical reasoning is rigorous in the sense that it does not generate any conclusion but ensures that the premises support the conclusion and act as reasons for believing it.[5][6] One central aspect is that this support is not restricted to a specific reasoner but that any rational person would find the conclusion convincing based on the premises.[6][1] This way, logical reasoning plays a role in expanding knowledge.[7]
The main discipline studying logical reasoning is called logic. It is divided into formal and informal logic, which study formal and informal logical reasoning.[8][9][10] Traditionally, logical reasoning was primarily associated with deductive reasoning studied by formal logic.[11] But in a wider sense, it also includes forms of non-deductive reasoning, such as inductive, abductive, and analogical reasoning.[12][13][14]
The forms of logical reasoning have in common that they use premises to make inferences in a norm-governed way. As norm-governed practices, they aim at inter-subjective agreement about the application of the norms, i.e. agreement about whether and to what degree the premises support their conclusion. The types of logical reasoning differ concerning the exact norms they use as well as the certainty of the conclusion they arrive at.[1][15] Deductive reasoning offers the strongest support and implies its conclusion with certainty, like mathematical proofs. For non-deductive reasoning, the premises make the conclusion more likely but do not ensure it. This support comes in degrees: strong arguments make the conclusion very likely, as is the case for well-researched issues in the empirical sciences.[1][16] Some theorists give a very wide definition of logical reasoning that includes its role as a cognitive skill responsible for high-quality thinking. In this regard, it has roughly the same meaning as critical thinking.[13][17]
Basic concepts[edit]
A variety of basic concepts is used in the study and analysis of logical reasoning. Logical reasoning happens by inferring a conclusion from a set of premises.[3] Premises and conclusions are normally seen as propositions. A proposition is a statement that makes a claim about what is the case. In this regard, propositions act as truth-bearers: they are either true or false.[18][19][3] For example, the sentence "The water is boiling." expresses a proposition since it can be true or false. The sentences "Is the water boiling?" or "Boil the water!", on the other hand, express no propositions since they are neither true nor false.[20][3] The propositions used as the starting point of logical reasoning are called the premises. The proposition inferred from them is called the conclusion.[18][19] For example, in the argument "all puppies are dogs; all dogs are animals; therefore all puppies are animals", the propositions "all puppies are dogs" and "all dogs are animals" act as premises while the proposition "all puppies are animals" is the conclusion.[21][22]
A set of premises together with a conclusion is called an argument.[23][3] An inference is the mental process of reasoning that starts from the premises and arrives at the conclusion.[18][24] But the terms "argument" and "inference" are often used interchangeably in logic. The purpose of arguments is to convince a person that something is the case by providing reasons for this belief.[25][26] Many arguments in natural language do not explicitly state all the premises. Instead, the premises are often implicitly assumed, especially if they seem obvious and belong to common sense.[25][27] Some theorists distinguish between simple and complex arguments. A complex argument is made up of many sub-arguments. This way, a chain is formed in which the conclusions of earlier arguments act as premises for later arguments. Each link in this chain has to be successful for a complex argument to succeed.[18][25]
An argument is correct or incorrect depending on whether the premises offer support for the conclusion. This is often understood in terms of probability: if the premises of a correct argument are true, it raises the probability that its conclusion is also true. Forms of logical reasoning can be distinguished based on how the premises support the conclusion. Deductive arguments offer the strongest possible support. Non-deductive arguments are weaker but are nonetheless correct forms of reasoning.[28][29] The term "proof" is often used for deductive arguments or very strong non-deductive arguments.[30] Incorrect arguments offer no or not sufficient support and are called fallacies,[31][32] although the use of incorrect arguments does not mean their conclusions are incorrect.[33]
Deductive reasoning[edit]
Deductive reasoning is the mental process of drawing deductive inferences. Deductively valid inferences are the most reliable form of inference: it is impossible for their conclusion to be false if all the premises are true.[34][35] This means that the truth of the premises ensures the truth of the conclusion. A deductive argument is sound if it is valid and all its premises are true.[36] For example, inferring the conclusion "no cats are frogs" from the premises "all frogs are amphibians" and "no cats are amphibians" is a sound argument. But even arguments with false premises can be deductively valid, like inferring that "no cats are frogs" from the premises "all frogs are mammals" and "no cats are mammals". In this regard, it only matters that the conclusion could not be false if the premises are true and not whether they actually are true.[37]
Deductively valid arguments follow a rule of inference.[38] A rule of inference is a scheme of drawing conclusions that depends only on the logical form of the premises and the conclusion but not on their specific content.[39][40] The most-discussed rule of inference is the modus ponens. It has the following form: p; if p then q; therefore q. This scheme is deductively valid no matter what p and q stand for.[41][5] For example, the argument "today is Sunday; if today is Sunday then I don't have to go to work today; therefore I don't have to go to work today" is deductively valid because it has the form of modus ponens.[42] Other popular rules of inference include modus tollens (not q; if p then q; therefore not p) and the disjunctive syllogism (p or q; not p; therefore q).[42][43]
The rules governing deductive reasoning are often expressed formally as logical systems for assessing the correctness of deductive arguments. Aristotelian logic is one of the earliest systems and was treated as the canon of logic in the Western world for over two thousand years. It is based on syllogisms, like concluding that "Socrates is a mortal" from the premises "Socrates is a man" and "all men are mortal".[44][45][46] The currently dominant system is known as classical logic and covers many additional forms of inferences besides syllogisms. So-called extended logics are based on classical logic and introduce additional rules of inference for specific domains. For example, modal logic can be used to reason about what is possible and what is necessary. Temporal logic can be used to draw inferences about what happened before, during, and after an event.[47][48][49] Classical logic and its extensions rest on a set of basic logical intuitions accepted by most logicians. They include the law of excluded middle, the double negation elimination, the principle of explosion, and the bivalence of truth.[50] So-called deviant logics reject some of these basic intuitions and propose alternative rules governing the validity of arguments.[44][51][52] For example, intuitionistic logics reject the law of excluded middle and the double negation elimination while paraconsistent logics reject the principle of explosion.[52][53][54]
Deductive reasoning plays a central role in formal logic and mathematics.[1] In mathematics, it is used to prove mathematical theorems based on a set of premises, usually called axioms. For example, Peano arithmetic is based on a small set of axioms from which all essential properties of natural numbers can be inferred using deductive reasoning.[55][56]
Non-deductive reasoning[edit]
Non-deductive reasoning is an important form of logical reasoning besides deductive reasoning. It happens in the form of inferences drawn from premises to reach and support a conclusion, just like its deductive counterpart. The hallmark of non-deductive reasoning is that this support is fallible. This means that if the premises are true, it makes it more likely but not certain that the conclusion is also true.[57][58] So for a non-deductive argument, it is possible for all its premises to be true while its conclusion is still false. There are various types of non-deductive reasoning, like inductive, abductive, and analogical reasoning.[1][59] Non-deductive reasoning is more common in everyday life than deductive reasoning.[60]
Non-deductive reasoning is ampliative and defeasible.[61][62] Sometimes, the terms non-deductive reasoning, ampliative reasoning, and defeasible reasoning are used synonymously even though there are slight differences in their meaning. Non-deductive reasoning is ampliative in the sense that it arrives at information not already present in the premises. Deductive reasoning, by contrast, is non-ampliative since it only extracts information already present in the premises without adding any additional information.[62][63][59] So with non-deductive reasoning, one can learn something new that one did not know before. But the fact that new information is added means that this additional information may be false. This is why non-deductive reasoning is not as secure as deductive reasoning.[58][64]
A closely related aspect is that non-deductive reasoning is defeasible or non-monotonic. This means that one may have to withdraw a conclusion upon learning new information. For example, if all birds a person has seen so far can fly, this person is justified in reaching the inductive conclusion that all birds fly. This conclusion is defeasible because the reasoner may have to revise it upon learning that penguins are birds that do not fly.[65][66][67]
Inductive[edit]

Inductive reasoning starts from a set of individual instances and uses generalization to arrive at a universal law governing all cases.[68][69][70] Some theorists use the term in a very wide sense to include any form of non-deductive reasoning, even if no generalization is involved.[69][71][68] In the more narrow sense, it can be defined as "the process of inferring a general law or principle from the observations of particular instances."[68] For example, starting from the empirical observation that "all ravens I have seen so far are black", inductive reasoning can be used to infer that "all ravens are black". In a slightly weaker form, induction can also be used to infer an individual conclusion about a single case, for example, that "the next raven I will see is black".[69][1] Inductive reasoning is closely related to statistical reasoning and probabilistic reasoning.[72] Like other forms of non-deductive reasoning, induction is not certain. This means that the premises support the conclusion by making it more probable but do not ensure its truth. In this regard, the conclusion of an inductive inference contains new information not already found in the premises.[68][60][1]
Various aspects of the premises are important to ensure that they offer significant support to the conclusion. In this regard, the sample size should be large to guarantee that many individual cases were considered before drawing the conclusion.[60][73] An intimately connected factor is that the sample is random and representative. This means that it includes a fair and balanced selection of individuals with different key characteristics. For example, when making a generalization about human beings, the sample should include members of different races, genders, and age groups.[60][74][75] A lot of reasoning in everyday life is inductive. For example, when predicting how a person will react to a situation, inductive reasoning can be employed based on how the person reacted previously in similar circumstances. It plays an equally central role in the sciences, which often start with many particular observations and then apply the process of generalization to arrive at a universal law.[76][77][1]
A well-known issue in the field of inductive reasoning is the so-called problem of induction. It concerns the question of whether or why anyone is justified in believing the conclusions of inductive inferences. This problem was initially raised by David Hume, who holds that future events need not resemble past observations. In this regard, inductive reasoning about future events seems to rest on the assumption that nature remains uniform.[78][79]
Abductive[edit]
Abductive reasoning is usually understood as an inference from an observation to a fact explaining this observation. Inferring that it has rained after seeing that the streets are wet is one example. Often, the expression "inference to the best explanation" is used as a synonym.[80][81][1] This expression underlines that there are usually many possible explanations of the same fact and that the reasoner should only infer the best explanation. For example, a tsunami could also explain why the streets are wet but this is usually not the best explanation. As a form of non-deductive reasoning, abduction does not guarantee the truth of the conclusion even if the premises are true.[80][82]
The more plausible the explanation is, the stronger it is supported by the premises. In this regard, it matters that the explanation is simple, i.e. does not include any unnecessary claims, and that it is consistent with established knowledge.[83][81][84] Other central criteria for a good explanation are that it fits observed and commonly known facts and that it is relevant, precise, and not circular. Ideally, the explanation should be verifiable by empirical evidence. If the explanation involves extraordinary claims then it requires very strong evidence.[84]

Abductive reasoning plays a central role in science when researchers discover unexplained phenomena. In this case, they often resort to a form of guessing to come up with general principles that could explain the observations. The hypotheses are then tested and compared to discover which one provides the best explanation.[85][84] This pertains particularly to cases of causal reasoning that try to discover the relation between causes and effects.[84] Abduction is also very common in everyday life. It is used there in a similar but less systematic form.[85][84] This relates, for example, to the trust people put in what other people say. The best explanation of why a person asserts a claim is usually that they believe it and have evidence for it. This form of abductive reasoning is relevant to why one normally trusts what other people say even though this inference is usually not drawn in an explicit way. Something similar happens when the speaker's statement is ambiguous and the audience tries to discover and explain what the speaker could have meant.[85] Abductive reasoning is also common in medicine when a doctor examines the symptoms of their patient in order to arrive at a diagnosis of their underlying cause.[1]
Analogical[edit]

Analogical reasoning involves the comparison of two systems in relation to their similarity. It starts from information about one system and infers information about another system based on the resemblance between the two systems.[88][89] Expressed schematically, arguments from analogy have the following form: (1) a is similar to b; (2) a has feature F; (3) therefore b probably also has feature F.[89][90] Analogical reasoning can be used, for example, to infer information about humans from medical experiments on animals: (1) rats are similar to humans; (2) birth control pills affect the brain development of rats; (3) therefore they may also affect the brain development of humans.[86]
Through analogical reasoning, knowledge can be transferred from one situation or domain to another. Arguments from analogy provide support for their conclusion but do not guarantee its truth. Their strength depends on various factors. The more similar the systems are, the more likely it is that a given feature of one object also characterizes the other object. Another factor concerns not just the degree of similarity but also its relevance. For example, an artificial strawberry made of plastic may be similar to a real strawberry in many respects, including its shape, color, and surface structure. But these similarities are irrelevant to whether the artificial strawberry tastes as sweet as the real one.[91]
Analogical reasoning plays a central role in problem-solving, decision-making, and learning. It can be used both for simple physical characteristics and complex abstract ideas.[92][93] In science, analogies are often used in models to understand complex phenomena in a simple way. For example, the Bohr model explains the interactions of sub-atomic particles in analogy to how planets revolve around the sun.[94][95]
Fallacies[edit]
A fallacy is an incorrect argument or a faulty form of reasoning. This means that the premises provide no or not sufficient support for the conclusion. Fallacies often appear to be correct on the first impression and thereby seduce people into accepting and using them. In logic, the term "fallacy" does not mean that the conclusion is false. Instead, it only means that some kind of error was committed on the way to reaching the conclusion. An argument can be a fallacy even if, by a fortuitous accident, the conclusion is true. Outside the field of logic, the term "fallacy" is sometimes used in a slightly different sense for a false belief or theory and not for an argument.[32][96][97]
Fallacies are usually divided into formal and informal fallacies. Formal fallacies are expressed in a formal language and usually belong to deductive reasoning. Their fault lies in the logical form of the argument, i.e. that it does not follow a valid rule of inference.[98][99] A well-known formal fallacy is affirming the consequent. It has the following form: (1) q; (2) if p then q; (3) therefore p. This fallacy is committed, for example, when a person argues that "the burglars entered by the front door" based on the premises "the burglars forced the lock" and "if the burglars entered by the front door, then they forced the lock".[100] This fallacy is similar to the valid rule of inference known as modus ponens. It is faulty because the first premise and the conclusion are switched around. Other well-known formal fallacies are denying the antecedent, affirming a disjunct, denying a conjunct, and the fallacy of the undistributed middle.[32][96][101]
Informal fallacies are expressed in natural language. Their main fault usually lies not in the form of the argument but has other sources, like its content or context.[96][99] Some informal fallacies, like some instances of false dilemmas and strawman fallacies, even involve correct deductive reasoning on the formal level.[97] The content of an argument is the idea that is expressed in it. For example, a false dilemma is an informal fallacy that is based on an error in one of the premises. The faulty premise oversimplifies reality: it states that things are either one way or another way but ignore many other viable alternatives.[102][103] False dilemmas are often used by politicians when they claim that either their proposal is accepted or there will be dire consequences. Such claims usually ignore that various alternatives exist to avoid those consequences, i.e. that their proposal is not the only viable solution.[104]
The strawman fallacy is another informal fallacy. Its error happens on the level of the context. It consists in misrepresenting the view of an opponent and then refuting this view. The refutation itself is often correct but the error lies in the false assumption that the opponent actually defends this view. For example, an alcohol lobbyist may respond to the suggestion to ban alcohol advertisements on television by claiming that it is impossible to make people give up drinking alcohol. This is a strawman fallacy since the suggestion was merely to ban advertisements and not to stop all alcohol consumption.[105][96][106]
Ambiguous and vague expressions in natural language are often responsible for the faulty reasoning in informal fallacies. For example, this is the case for fallacies of ambiguity, like the argument "(1) feathers are light; (2) light is opposed to darkness; (3) therefore feathers are opposed to darkness". The error is found in the ambiguous term "light", which has one meaning in the first premise ("not heavy") and a different meaning in the second premise ("visible electromagnetic radiation").[107][108][109]
As a skill[edit]
Some theorists discuss logical reasoning in a very wide sense that includes its role as a broad skill responsible for high-quality thinking. In this sense, it is roughly equivalent to critical thinking and includes the capacity to select and apply the appropriate rules of logic to specific situations.[110] It encompasses a great variety of abilities besides drawing conclusions from premises. Examples are to understand a position, to generate and evaluate reasons for and against it as well as to critically assess whether to accept or reject certain information. It is about making judgments and drawing conclusions after careful evaluation and contrasts in this regard with uncritical snap judgments and gut feelings.[17] Other core skills linked to logical reasoning are to assess reasons before accepting a claim and to search for new information if more is needed to reach a reliable conclusion. It also includes the ability to consider different courses of action and compare the advantages and disadvantages of their consequences, to use common sense, and to avoid inconsistencies.[111][112] The skills responsible for logical reasoning can be learned, trained, and improved.[17][113]
Logical reasoning is relevant both on the theoretical and practical level.[114][115] On the theoretical level, it helps decrease the number of false beliefs. A central aspect concerns the abilities used to distinguish facts from mere opinions, like the process of finding and evaluating reasons for and against a position to come to one's own conclusion.[114] This includes being able to differentiate between reliable and unreliable sources of information. This matters for effective reasoning since it is often necessary to rely on information provided by other people instead of checking every single fact for oneself. [116][117] This way, logical reasoning can help the person avoid the effects of propaganda or being manipulated by others.[118][119] When important information is missing, it is often better to suspend judgment than to jump to conclusions.[118] In this regard, logical reasoning should be skeptical and open-minded at the same time.[120]
On the practical level, logical reasoning concerns the issue of making rational and effective decisions.[114][115] For many real-life decisions, various courses of action are available to the agent. For each possible action, there can be conflicting reasons, some in favor of it and others opposed to it. In such cases, logical reasoning includes weighing the potential benefits and drawbacks as well as considering their likelihood in order to arrive at a balanced all-things-considered decision.[121][122] For example, when a person runs out of drinking water in the middle of a hiking trip, they could employ the skills associated with logical reasoning to decide whether to boil and drink water from a stream that might contain dangerous microorganisms rather than break off the trip and hike back to the parking lot. This could include considering factors like assessing how dangerous the microorganisms are and the likelihood that they survive the boiling procedure. It may also involve gathering relevant information to make these assessments, for example, by asking other hikers.[123]
Time also plays a central role in logical reasoning.[124] If one lacks important information, it is often better to delay a decision and look for new information before coming to a conclusion.[111] If the decision is time-sensitive, on the other hand, logical reasoning may imply making a fast decision based on the currently available evidence even if it is very limited. For example, if a friend yells "Duck!" during a baseball game the most logical response may be to blindly trust them and duck instead of demanding an explanation or investigating what might have prompted their exclamation.[124][125] Generally speaking, the less time there is, the more significant it is to trust intuitions and gut feelings. If there is more time, on the other hand, it becomes important to examine ambiguities and assess contradictory information.[126]
See also[edit]
- Argumentation theory
- Dialogical logic
- Epilogism
- List of rules of inference
- Transduction (machine learning)
- Transduction (psychology)
References[edit]
Citations[edit]
- ^ a b c d e f g h i j k Nunes 2011, p. 2066–9, Logical Reasoning and Learning.
- ^ Bronkhorst et al. 2020, p. 1675.
- ^ a b c d e Dowden 2020, p. 24.
- ^ Bronkhorst et al. 2020, p. 1676.
- ^ a b Franks et al. 2013, p. 146.
- ^ a b Dowden 2020, p. 5.
- ^ Chang 2014, p. 37.
- ^ Haack 1978, p. 1–10, 1. 'Philosophy of logics'.
- ^ Dowden 2020, p. 355.
- ^ Girod 2014, p. 13.
- ^ Craig 1996, Formal and informal logic.
- ^ Bronkhorst et al. 2020, p. 1674-6.
- ^ a b Enyeart, Baker & Vanharlingen 1980, p. 263–267.
- ^ Flick 2013, p. 123.
- ^ Dowden 2020, p. 5, 432.
- ^ Dowden 2020, p. 346-7, 432, 470.
- ^ a b c Dowden 2020, p. 1.
- ^ a b c d Audi 1999, Philosophy of logic.
- ^ a b Honderich 2005, philosophical logic.
- ^ Copi, Cohen & Rodych 2018, p. 4.
- ^ Kenny 2018, p. 140.
- ^ Kaye 2012, p. 57.
- ^ Johnson 2017, p. 2.
- ^ a b c Dowden 2020, p. 67-8.
- ^ Gabbay 2002, p. 15.
- ^ Bronkhorst et al. 2020, p. 1676-7.
- ^ Dowden 2020, p. 67-8, 432, 470.
- ^ Copi, Cohen & Rodych 2018, p. 22–6.
- ^ Dowden 2020, p. 31-2, 67-8.
- ^ Girod 2014, p. 54.
- ^ a b c Hansen 2020.
- ^ Arp, Barbone & Bruce 2018, p. 115.
- ^ Johnson-Laird 2009, p. 8–17.
- ^ Dowden 2020, p. 432.
- ^ Evans 2005, 8. Deductive reasoning.
- ^ Evans 2005, p. 169, 8. Deductive Reasoning.
- ^ Byrne, Evans & Newstead 2019, p. 59.
- ^ Dowden 2020, p. 392.
- ^ Jamieson 2013, p. 34.
- ^ a b Velleman 2006, p. 8, 103.
- ^ Church 1996, p. 104.
- ^ a b Jacquette 2006, p. 1–12, Introduction: Philosophy of logic today.
- ^ Smith 2020.
- ^ Groarke 2022.
- ^ Haack 1978, p. 170, 222.
- ^ Norman & Sylvan 2012, p. 419.
- ^ Goranko & Rumberg 2022.
- ^ Shapiro & Kouri Kissel 2021.
- ^ Haack 1996, p. 1, 4, 1. 'Alternative' in 'Alternative Logic'.
- ^ a b Borchert 2006, Logic, Non-Classical.
- ^ Moschovakis 2021.
- ^ Priest, Tanaka & Weber 2018.
- ^ Weaver 2015, p. 70.
- ^ Sayward 2009, p. 15.
- ^ Dowden 2020, p. 432, 470.
- ^ a b Anshakov & Gergely 2010, p. 128.
- ^ a b Magnani & Bertolotti 2017, p. 152.
- ^ a b c d Dowden 2020, p. 470.
- ^ Amaya 2015, p. 202.
- ^ a b Bertolaso & Sterpetti 2020, p. 110.
- ^ Cellucci 2017, p. 154.
- ^ Nadler & Shapiro 2021, p. 81.
- ^ Koons 2022.
- ^ Nute 2012, p. 82.
- ^ Niiniluoto, Sintonen & Wolenski 2004, p. 901.
- ^ a b c d Li & Vitányi 2019, p. 345–448, Inductive Reasoning.
- ^ a b c Vickers 2022.
- ^ Porta 2016, Inductive Reasoning.
- ^ Dowden 2020, p. 432, 450, 470.
- ^ Bird 2006, p. 123.
- ^ Lorenzano, Rheinberger & Galles 2010, p. 103.
- ^ Mizrahi 2020, p. 83.
- ^ Asher, Banks & Scheuren 2007, p. 22.
- ^ Heit 2007, p. 1–24, What Is Induction and Why Study It?.
- ^ Dowden 2020, p. 346-7, 432.
- ^ Henderson 2022.
- ^ Psillos 2023.
- ^ a b Douven 2022.
- ^ a b Koslowski 2017, p. 366–382, Abductive reasoning and explanation.
- ^ Walton 2014, p. 1–3.
- ^ Douven 2011, Explicating Abduction.
- ^ a b c d e Dowden 2020, p. 519-20.
- ^ a b c Douven 2011, 1.2 The ubiquity of abduction.
- ^ a b Salmon 2012, p. 132–3.
- ^ Kurtz, Morris & Pershadsingh 1989, p. 896–901.
- ^ Bunnin & Yu 2008, p. 25.
- ^ a b Bartha 2019.
- ^ Sandkühler 2010, Analogie.
- ^
- Salmon 2012, p. 133–4
- Bartha 2022
- Goswami 2013, p. 86
- Sriram 2012, p. 286
- ^ Fasko & Fair 2020, p. 51.
- ^ Demir 2017, p. 32.
- ^ Margolis et al. 1986, p. 167.
- ^ Ornek & Saleh 2012, p. 82.
- ^ a b c d Dowden 2023.
- ^ a b Dowden 2020, p. 290.
- ^ Kilcrease 2021, p. 100.
- ^ a b Vleet 2011, p. ix.
- ^ Kohar 2016, p. 54, 57.
- ^ Tomić 2013, p. 347–368.
- ^ Dowden 2021.
- ^ Tuman 2008, p. 75.
- ^ Walton 2013, p. 250–2.
- ^ Walton 1987, p. 10.
- ^ Engel 2014, p. 74, 108–11.
- ^ Mackie 2006, Fallacies.
- ^ Atwater 1867, p. 167.
- ^
- Enyeart, Baker & Vanharlingen 1980, p. 263–267
- Dowden 2020, p. 1
- Bronkhorst et al. 2020, p. 1674
- Ivory 2021, p. 73
- Halpern 2014, p. 81
- ^ a b Dowden 2020, p. 18.
- ^ Nelson 2005, p. 167.
- ^ Conati et al. 2015, p. 738.
- ^ a b c Dowden 2020, p. 1, 13.
- ^ a b Mele & Rawling 2004, p. 3–14, Introduction: Aspects of Rationality.
- ^ Dowden 2020, p. 143, 172.
- ^ Cottrell 2017, p. 110.
- ^ a b Dowden 2020, p. 263-4.
- ^ Gambrill 2012, p. 540.
- ^ Dowden 2020, p. 19.
- ^ Dowden 2020, p. 6.
- ^ Robertson 2009, p. 192.
- ^ Dowden 2020, p. 2-5.
- ^ a b Dowden 2020, p. 9.
- ^ Viale 2020, p. 746.
- ^ Dowden 2020, p. 10.
Sources[edit]
- Amaya, Amalia (30 April 2015). The Tapestry of Reason: An Inquiry into the Nature of Coherence and its Role in Legal Argument. Bloomsbury Publishing. p. 202. ISBN 9781782255161.
- Anshakov, Oleg M.; Gergely, Tamás (11 March 2010). Cognitive Reasoning: A Formal Approach. Springer Science & Business Media. p. 128. ISBN 9783540688754.
- Arp, Robert; Barbone, Steven; Bruce, Michael (28 September 2018). Bad Arguments: 100 of the Most Important Fallacies in Western Philosophy. John Wiley & Sons. p. 115. ISBN 978-1-119-16580-4.
- Asher, Jana; Banks, David; Scheuren, Fritz J. (26 December 2007). Statistical Methods for Human Rights. Springer Science & Business Media. p. 22. ISBN 9780387728377.
- Atwater, Lyman Hotchkiss (1867). Manual of Elementary Logic: Designed Especially for the Use of Teachers and Learners. J. B. Lippincott. p. 167.
- Audi, Robert (1999). "Philosophy of logic". The Cambridge Dictionary of Philosophy. Cambridge University Press. ISBN 9781107643796. Archived from the original on 14 April 2021. Retrieved 29 December 2021.
- Bartha, Paul (2019). "Analogy and Analogical Reasoning". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 21 January 2021.
- Bartha, Paul (2022). "Analogy and Analogical Reasoning: 2.4 Analogical inference rules?". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 19 January 2023.
- Bertolaso, Marta; Sterpetti, Fabio (5 February 2020). A Critical Reflection on Automated Science: Will Science Remain Human?. Springer Nature. p. 110. ISBN 9783030250010.
- Bird, Alexander (9 May 2006). Philosophy Of Science. Routledge. p. 123. ISBN 9781135364236.
- Blackburn, Simon (24 March 2016). "rule of inference". A Dictionary of Philosophy. Oxford University Press. p. 422. ISBN 9780198735304. Archived from the original on 8 January 2022. Retrieved 8 January 2022.
- Blackburn, Simon (1 January 2008). "argument". The Oxford Dictionary of Philosophy. Oxford University Press. p. 29. ISBN 9780199541430. Archived from the original on 8 January 2022. Retrieved 8 January 2022.
- Borchert, Donald (2006). "Logic, Non-Classical". Macmillan Encyclopedia of Philosophy, 2nd Edition. Macmillan. ISBN 9780028657905.
- Bronkhorst, Hugo; Roorda, Gerrit; Suhre, Cor; Goedhart, Martin (December 2020). "Logical Reasoning in Formal and Everyday Reasoning Tasks". International Journal of Science and Mathematics Education. 18 (8): 1673–1694. Bibcode:2020IJSME..18.1673B. doi:10.1007/s10763-019-10039-8. S2CID 254541202.
- Bunnin, Nicholas; Yu, Jiyuan (15 April 2008). The Blackwell Dictionary of Western Philosophy. Wiley. p. 25. ISBN 9780470997215.
- Byrne, Ruth M. J.; Evans, Jonathan St B. T.; Newstead, Stephen E. (18 June 2019). Human Reasoning: The Psychology Of Deduction. Routledge. p. 59. ISBN 9781317716266.
- Cellucci, Carlo (29 March 2017). Rethinking Knowledge: The Heuristic View. Springer. p. 154. ISBN 9783319532370.
- Chang, Mark (22 July 2014). Principles of Scientific Methods. CRC Press. p. 37. ISBN 9781482238099.
- Church, Alonzo (1996). Introduction to Mathematical Logic. Princeton University Press. p. 104. ISBN 9780691029061.
- Colman, Andrew M. (1 January 2009). "affirming the consequent". A Dictionary of Psychology. Oxford University Press. ISBN 9780199534067.
- Conati, Cristina; Heffernan, Neil; Mitrovic, Antonija; Verdejo, M. Felisa (16 June 2015). Artificial Intelligence in Education: 17th International Conference, AIED 2015, Madrid, Spain, June 22-26, 2015. Proceedings. Springer. p. 738. ISBN 9783319197739.
- Copi, Irving M.; Cohen, Carl; Rodych, Victor (3 September 2018). Introduction to Logic. Routledge. ISBN 9781351386975.
- Cottrell, Stella (14 March 2017). Critical Thinking Skills: Effective Analysis, Argument and Reflection. Bloomsbury Publishing. p. 110. ISBN 9781350314672.
- Craig, Edward (1996). "Formal and informal logic". Routledge Encyclopedia of Philosophy. Routledge. ISBN 9780415073103. Archived from the original on 16 January 2021. Retrieved 29 December 2021.
- Demir, Imran (24 March 2017). Overconfidence and Risk Taking in Foreign Policy Decision Making: The Case of Turkey's Syria Policy. Springer. p. 32. ISBN 9783319526058.
- Douven, Igor (2022). "Abduction and Explanatory Reasoning". Oxford Bibliographies. Oxford University Press. Retrieved 18 January 2023.
- Douven, Igor (9 March 2011). "Abduction". Stanford Encyclopedia of Philosophy. Retrieved 18 January 2023.
- Dowden, Bradley (2023). "Fallacies". Internet Encyclopedia of Philosophy. Retrieved 22 January 2023.
- Dowden, Bradley (2021). "Fallacies: 6. Partial List of Fallacies". Internet Encyclopedia of Philosophy. Retrieved 13 March 2021.
- Dowden, Bradley H. (2020). Logical Reasoning (PDF). (for an earlier version, see: Dowden, Bradley Harris (1993). Logical Reasoning. Wadsworth Publishing Company. ISBN 9780534176884.)
- Engel, S. Morris (2014). With Good Reason an Introduction to Informal Fallacies. St. Martin's Press. pp. 74, 108–11. ISBN 9781457695957.
- Enyeart, Morris A.; Baker, Dale; Vanharlingen, Dave (May 1980). "Correlation of inductive and deductive logical reasoning to college physics achievement". Journal of Research in Science Teaching. 17 (3): 263–267. Bibcode:1980JRScT..17..263E. doi:10.1002/tea.3660170311.
- Evans, Jonathan (18 April 2005). Morrison, Robert (ed.). The Cambridge Handbook of Thinking and Reasoning. Cambridge University Press. ISBN 9780521824170.
- Fasko, Daniel; Fair, Frank (12 October 2020). Critical Thinking and Reasoning: Theory, Development, Instruction, and Assessment. Brill. p. 51. ISBN 9789004444591.
- Flick, Uwe (10 December 2013). The SAGE Handbook of Qualitative Data Analysis. SAGE. p. 123. ISBN 9781446296691.
- Franks, Bridget A.; Therriault, David J.; Buhr, Miriam I.; Chiang, Evelyn S.; Gonzalez, Claire M.; Kwon, Heekyung K.; Schelble, Jenni L.; Wang, Xuesong (August 2013). "Looking back: reasoning and metacognition with narrative texts". Metacognition and Learning. 8 (2): 146. doi:10.1007/s11409-013-9099-2. S2CID 255162310.
- Gabbay, Michael (4 September 2002). Logic With Added Reasoning. Broadview Press. p. 15. ISBN 9781551114057.
- Gambrill, Eileen (1 May 2012). Critical Thinking in Clinical Practice: Improving the Quality of Judgments and Decisions. John Wiley & Sons. p. 540. ISBN 9780470904381.
- Girod, Robert J. (25 September 2014). Logical Investigative Methods: Critical Thinking and Reasoning for Successful Investigations. CRC Press. ISBN 9781482243147.
- Goranko, Valentin; Rumberg, Antje (2022). "Temporal Logic". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 24 January 2023.
- Goswami, Usha (23 October 2013). Analogical Reasoning in Children. Routledge. p. 86. ISBN 9781317775393.
- Groarke, Louis F. (2022). "Aristotle: Logic". Internet Encyclopedia of Philosophy. Archived from the original on 29 December 2021. Retrieved 1 January 2022.
- Haack, Susan (1996). "1. 'Alternative' in 'Alternative Logic'". Deviant Logic, Fuzzy Logic: Beyond the Formalism. Chicago and London: University of Chicago Press. pp. 1, 4. ISBN 9780226311333.
- Haack, Susan (27 July 1978). Philosophy of Logics. Cambridge University Press. ISBN 9780521293297.
- Halpern, Diane F. (4 February 2014). Critical Thinking Across the Curriculum: A Brief Edition of Thought & Knowledge. Routledge. p. 81. ISBN 9781317778370.
- Hansen, Hans (2020). "Fallacies". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on 29 March 2021. Retrieved 18 March 2021.
- Heit, Evan (2007). "What Is Induction and Why Study It?". Inductive Reasoning: Experimental, Developmental, and Computational Approaches. Cambridge University Press. pp. 1–24. ISBN 9780521856485.
- Henderson, Leah (2022). "The Problem of Induction: 1. Hume's Problem". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 18 January 2023.
- Honderich, Ted (2005). "philosophical logic". The Oxford Companion to Philosophy. Oxford University Press. ISBN 9780199264797. Archived from the original on 29 January 2021. Retrieved 2 January 2022.
- Ivory, Sarah Birrell (11 January 2021). Becoming a Critical Thinker: For Your University Studies and Beyond. Oxford University Press. p. 73. ISBN 9780198841531.
- Jacquette, Dale (2006). "Introduction: Philosophy of logic today". Philosophy of Logic. North Holland. pp. 1–12. ISBN 9780444515414. Archived from the original on 7 December 2021. Retrieved 29 December 2021.
- Jamieson, D. (9 March 2013). Language, Mind, and Art: Essays in Appreciation and Analysis, in Honor of Paul Ziff. Springer Science & Business Media. p. 34. ISBN 9789401583138.
- Johnson, Gregory (6 January 2017). Argument and Inference: An Introduction to Inductive Logic. MIT Press. p. 2. ISBN 9780262035255.
- Johnson-Laird, Phil (30 December 2009). "Deductive reasoning". WIREs Cognitive Science. 1 (1): 8–17. doi:10.1002/wcs.20. ISSN 1939-5078. PMID 26272833.
- Kaye, Sharon M. (1 December 2012). Critical Thinking: A Beginner's Guide. Simon and Schuster. p. 57. ISBN 9781780741475.
- Kenny, Anthony (15 October 2018). An Illustrated Brief History of Western Philosophy, 20th Anniversary Edition. John Wiley & Sons. p. 140. ISBN 9781119531173.
- Kilcrease, Bethany (2021). Falsehood and Fallacy: How to Think, Read, and Write in the Twenty-First Century. University of Toronto Press. p. 100. ISBN 9781487588618.
- Kohar, Richard (15 June 2016). Basic Discrete Mathematics: Logic, Set Theory, And Probability. World Scientific Publishing Company. pp. 54, 57. ISBN 9789814730419.
- Koons, Robert (2022). "Defeasible Reasoning". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 22 January 2023.
- Koslowski, Barbara (14 November 2017). "Abductive reasoning and explanation". International Handbook of Thinking and Reasoning. Routledge. pp. 366–382. doi:10.4324/9781315725697. ISBN 9781315725697.
- Kurtz, T W; Morris, R C; Pershadsingh, H A (June 1989). "The Zucker fatty rat as a genetic model of obesity and hypertension". Hypertension. 13 (6_pt_2): 896–901. doi:10.1161/01.HYP.13.6.896. PMID 2786848. S2CID 109606.
- Li, Ming; Vitányi, Paul (2019). "Inductive Reasoning". An Introduction to Kolmogorov Complexity and Its Applications. Texts in Computer Science. Springer International Publishing. pp. 345–448. doi:10.1007/978-3-030-11298-1_5. ISBN 9783030112981.
- Lorenzano, Pablo; Rheinberger, Hans-Jörg; Galles, Eduardo Ortiz and Carlos Delfino (27 September 2010). History and Philosophy of Science and Technology. Eolss Publishers / UNESCO. p. 103. ISBN 9781848263239.
- Mackie, J. L. (2006). "Fallacies". In Borchert, Donald (ed.). Macmillan Encyclopedia of Philosophy, 2nd Edition. Macmillan. ISBN 9780028657905.
- Magnani, Lorenzo; Bertolotti, Tommaso (22 May 2017). Springer Handbook of Model-Based Science. Springer. p. 152. ISBN 9783319305264.
- Margolis, James M.; Margolis, Joseph; Krausz, Michael; Krausz, A. S.; Burian, R.; Margolis, Professor Joseph (31 October 1986). Rationality, Relativism and the Human Sciences. Springer Science & Business Media. p. 167. ISBN 9789024732715.
- Mele, Alfred R.; Rawling, Piers. (2004). "INTRODUCTION: Aspects of Rationality". The Oxford Handbook of Rationality. Oxford University Press. pp. 3–14. doi:10.1093/0195145399.001.0001. ISBN 9780195145397.
- Mizrahi, Moti (29 September 2020). The Relativity of Theory: Key Positions and Arguments in the Contemporary Scientific Realism/Antirealism Debate. Springer Nature. p. 83. ISBN 9783030580476.
- Moschovakis, Joan (2021). "Intuitionistic Logic: 1. Rejection of Tertium Non Datur". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 11 December 2021.
- Nadler, Steven; Shapiro, Lawrence (31 August 2021). When Bad Thinking Happens to Good People: How Philosophy Can Save Us from Ourselves. Princeton University Press. p. 81. ISBN 9780691220086.
- Nelson, Hazel E. (2005). Cognitive-behavioural Therapy with Delusions and Hallucinations: A Practice Manual. Nelson Thornes. p. 167. ISBN 9780748792566.
- Niiniluoto, I.; Sintonen, Matti; Wolenski, Jan (31 March 2004). Handbook of Epistemology. Springer Science & Business Media. p. 901. ISBN 9781402019852.
- Norman, J.; Sylvan, R. (6 December 2012). Directions in Relevant Logic. Springer Science & Business Media. p. 419. ISBN 9789400910058.
- Nunes, Terezinha (5 October 2011). "Logical Reasoning and Learning". In Seel, Norbert M. (ed.). Encyclopedia of the Sciences of Learning. Springer Science & Business Media. pp. 2066–9. ISBN 9781441914279.
- Nute, Donald (6 December 2012). Defeasible Deontic Logic. Springer Science & Business Media. p. 82. ISBN 9789401588515.
- Ornek, Dr Funda; Saleh, Dr Issa M. (1 May 2012). Contemporary Science Teaching Approaches: Promoting Conceptual Understanding in Science. IAP. p. 82. ISBN 9781617356100.
- Porta, Miquel (21 July 2016). "Inductive Reasoning". A Dictionary of Epidemiology. Oxford University Press. ISBN 9780199976720.
- Priest, Graham; Tanaka, Koji; Weber, Zach (2018). "Paraconsistent Logic". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Retrieved 14 December 2021.
- Psillos, Stathis (2023). "Induction, The Problem of". Internet Encyclopedia of Philosophy. Retrieved 22 January 2023.
- Robertson, Simon (1 October 2009). Spheres of Reason: New Essays in the Philosophy of Normativity. OUP Oxford. p. 192. ISBN 9780191610219.
- Salmon, Merrilee (2012). Introduction to Logic and Critical Thinking. Cengage Learning. ISBN 978-1133711643.
- Sandkühler, Hans Jörg (2010). "Analogie". Enzyklopädie Philosophie. Meiner. ISBN 9783787319992. Archived from the original on 2021-03-11. Retrieved 2023-01-24.
- Sayward, Charles (2009). Dialogues Concerning Natural Numbers. Peter Lang. p. 15. ISBN 9781433107801.
- Shapiro, Stewart; Kouri Kissel, Teresa (2021). "Classical Logic". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on 3 May 1998. Retrieved 4 December 2021.
- Smith, Robin (2020). "Aristotle's Logic". The Stanford Encyclopedia of Philosophy. Metaphysics Research Lab, Stanford University. Archived from the original on 26 December 2021. Retrieved 1 January 2022.
- Sriram, Ram D. (6 December 2012). Intelligent Systems for Engineering: A Knowledge-based Approach. Springer Science & Business Media. p. 286. ISBN 9781447106319.
- Tomić, Taeda (2013). "False Dilemma: A Systematic Exposition". Argumentation. 27 (4): 347–368. doi:10.1007/s10503-013-9292-0. S2CID 144781912.
- Tuman, Joseph S. (2008). Political Communication in American Campaigns. SAGE. p. 75. ISBN 9781412909457.
- Velleman, Daniel J. (16 January 2006). How to Prove It: A Structured Approach. Cambridge University Press. p. 8, 103. ISBN 9780521675994.
- Viale, Riccardo (2 December 2020). Routledge Handbook of Bounded Rationality. Routledge. p. 746. ISBN 9781317330790.
- Vickers, John M. (2022). "Inductive Reasoning". Oxford Bibliographies. Oxford University Press. Retrieved 18 January 2023.
- Vleet, Jacob E. Van (2011). Informal Logical Fallacies: A Brief Guide. University Press of America. p. ix. ISBN 9780761854333.
- Walton, Douglas (15 May 2014). Abductive Reasoning. University of Alabama Press. pp. 1–3. ISBN 9780817357825.
- Walton, Douglas (26 August 2013). Methods of Argumentation. Cambridge University Press. pp. 250–2. ISBN 9781107039308.
- Walton, Douglas N. (1987). Informal Fallacies: Towards a Theory of Argument Criticisms. John Benjamins Publishing. p. 10. ISBN 9789027250056.
- Weaver, Nik (22 April 2015). Truth And Assertibility. World Scientific. p. 70. ISBN 9789814619981.