Lorraine Foster

Lorraine L. Foster
Lorraine L. Foster
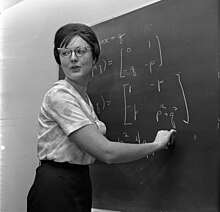	Dr. Foster in 1964. (Photo from the Los Angeles Times Photographic Collection, UCLA Library Digital Collections)
Born	December 25, 1938; Culver City, California
Citizenship	American
Education	B.A. 1960, Occidental College; Ph.D. 1964, California Institute of Technology
Occupation	Mathematician
Employer	California State University, Northridge

Lorraine Lois Foster (December 25, 1938, Culver City, California) is an American mathematician. In 1964 she became the first woman to receive a Ph.D. in mathematics from California Institute of Technology.^[1] Her thesis advisor at Caltech was Olga Taussky-Todd.^[2] Foster's Erdos number is 2.

Born Lorraine Lois Turnbull, she attended Occidental College where she majored in physics. She was admitted to Caltech after receiving a Woodrow Wilson Foundation fellowship. In 1964 she joined the faculty of California State University, Northridge. She works in number theory and the theory of mathematical symmetry.

Selected bibliography

Foster, L. (1966). On the characteristic roots of the product of certain rational integral matrices of order two. Pacific Journal of Mathematics, 18(1), 97–110. http://doi.org/10.2140/pjm.1966.18.97
Brenner, J. L., & Foster, L. L. (1982). Exponential diophantine equations. Pacific Journal of Mathematics, 101(2), 263–301.
Alex, L. J., & Foster, L. L. (1983). On diophantine equations of the form $1+2^{a}=p^{b}q^{c}+2^{d}p^{e}q^{f}$ . Rocky Mountain Journal of Mathematics, 13(2), 321–332. http://doi.org/10.1216/RMJ-1983-13-2-321
Alex, L. J., & Foster, L. L. (1985). On the Diophantine equation $1+p^{a}=2+2^{b}+2^{c}p^{d}$ . Rocky Mountain Journal of Mathematics, 15(3), 739–762. http://doi.org/10.1216/RMJ-1985-15-3-739
L. Foster (1989). Finite Symmetry Groups in Three Dimensions, CSUN Instructional Media Center, Jan. 1989 (video, 27 minutes).
L. Foster (1990). Archimedean and Archimedean Dual Polyhedra, CSUN Instructional Media Center, Feb. 1990 (video, 47 minutes). https://www.worldcat.org/title/archimedean-and-archimedean-dual-polyhedra/oclc/63936926&referer=brief_results
Foster, L. L. (1990). On the symmetry group of the dodecahedron. Mathematics Magazine, 63, 106–107.
Foster, L. L. (1991). Convex Polyhedral Models for the Finite Three-Dimensional Isometry Groups. The Mathematical Heritage of CF Gauss, pp 267–281.
L. Foster (1991). The Alhambra Past and Present—a Geometer’s Odyssey Part 1, CSUN Instructional Media Center, December 1991 (video, 40 minutes).
L. Foster (1991). The Alhambra Past and Present—a Geometer’s Odyssey Part 2, CSUN Instructional Media Center, December 1991 (video, 40 minutes). https://www.worldcat.org/title/alhambra-past-and-present-a-geometers-odyssey-parts-1-and-2/oclc/28680624?loc=94043&tab=holdings&start_holding=7
Foster, L. L. (1991). Convex polyhedral models for the finite three-dimensional isometry groups. In G. M. Rassias (Ed.), The Mathematical Heritage of C F Gauss (pp. 267–281). Singapore: World Scientific.
L. Foster (1992). Regular-Faced Polyhedra—an Introduction, CSUN Instructional Media Center, Dec. 1992 (video, 47 minutes)
Alex, L. J., & Foster, L. L. (1992). On the Diophantine equation ${\bf {1+x+y=z}}$ . Rocky Mountain Journal of Mathematics, 22(1), 11–62. http://doi.org/10.1216/rmjm/1181072793
Alex, L. J., & Foster, L. L. (1995). On the Diophantine equation $w+x+y=z$ , with $wxyz=2^{r}3^{s}5^{t}$ . Rev. Mat. Univ. Complut. Madrid, 8(1), 13–48.