Maximal subgroup
This article needs additional citations for verification. (December 2009) |
In mathematics, the term maximal subgroup is used to mean slightly different things in different areas of algebra.
In group theory, a maximal subgroup H of a group G is a proper subgroup, such that no proper subgroup K contains H strictly. In other words, H is a maximal element of the partially ordered set of subgroups of G that are not equal to G. Maximal subgroups are of interest because of their direct connection with primitive permutation representations of G. They are also much studied for the purposes of finite group theory: see for example Frattini subgroup, the intersection of the maximal subgroups.
In semigroup theory, a maximal subgroup of a semigroup S is a subgroup (that is, a subsemigroup which forms a group under the semigroup operation) of S which is not properly contained in another subgroup of S. Notice that, here, there is no requirement that a maximal subgroup be proper, so if S is in fact a group then its unique maximal subgroup (as a semigroup) is S itself. Considering subgroups, and in particular maximal subgroups, of semigroups often allows one to apply group-theoretic techniques in semigroup theory.[citation needed] There is a one-to-one correspondence between idempotent elements of a semigroup and maximal subgroups of the semigroup: each idempotent element is the identity element of a unique maximal subgroup.
Existence of maximal subgroup[edit]
Any proper subgroup of a finite group is contained in some maximal subgroup, since the proper subgroups form a finite partially ordered set under inclusion. There are, however, infinite abelian groups that contain no maximal subgroups, for example the Prüfer group.
Maximal normal subgroup[edit]
Similarly, a normal subgroup N of G is said to be a maximal normal subgroup (or maximal proper normal subgroup) of G if N < G and there is no normal subgroup K of G such that N < K < G. We have the following theorem:
- Theorem: A normal subgroup N of a group G is a maximal normal subgroup if and only if the quotient G/N is simple.
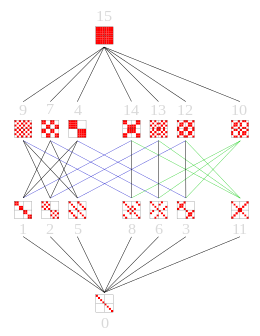
Hasse diagrams[edit]
These Hasse diagrams show the lattices of subgroups of the symmetric group S4, the dihedral group D4, and C23, the third direct power of the cyclic group C2.
The maximal subgroups are linked to the group itself (on top of the Hasse diagram) by an edge of the Hasse diagram.
 |
 |
 |
