Moment of inertia factor
In planetary sciences, the moment of inertia factor or normalized polar moment of inertia is a dimensionless quantity that characterizes the radial distribution of mass inside a planet or satellite. Since a moment of inertia has dimensions of mass times length squared, the moment of inertia factor is the coefficient that multiplies these.
Definition[edit]
For a planetary body with principal moments of inertia , the moment of inertia factor is defined as
- ,
where C is the first principal moment of inertia of the body, M is the mass of the body, and R is the mean radius of the body.[1][2] For a sphere with uniform density, .[note 1][note 2] For a differentiated planet or satellite, where there is an increase of density with depth, . The quantity is a useful indicator of the presence and extent of a planetary core, because a greater departure from the uniform-density value of 2/5 conveys a greater degree of concentration of dense materials towards the center.
Solar System values[edit]
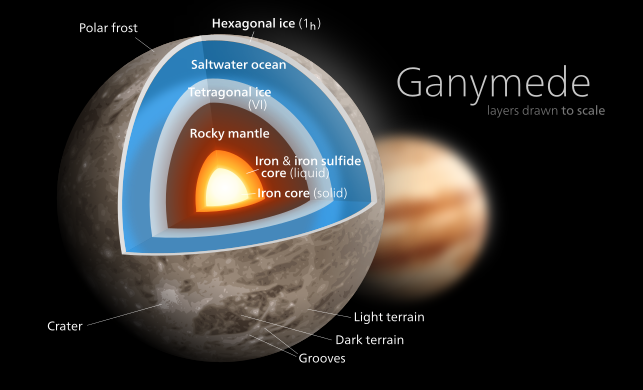
The Sun has by far the lowest moment of inertia factor value among Solar System bodies; it has by far the highest central density (162 g/cm3,[3][note 3] compared to ~13 for Earth[4][5]) and a relatively low average density (1.41 g/cm3 versus 5.5 for Earth). Saturn has the lowest value among the gas giants in part because it has the lowest bulk density (0.687 g/cm3).[6] Ganymede has the lowest moment of inertia factor among solid bodies in the Solar System because of its fully differentiated interior,[7][8] a result in part of tidal heating due to the Laplace resonance,[9] as well as its substantial component of low density water ice. Callisto is similar in size and bulk composition to Ganymede, but is not part of the orbital resonance and is less differentiated.[7][8] The Moon is thought to have a small core, but its interior is otherwise relatively homogenous.[10][11]
| Body | Value | Source | Notes |
|---|---|---|---|
| Sun | 0.070 | [3] | Not measured |
| Mercury | 0.346 ± 0.014 | [12] | |
| Venus | 0.337 ± 0.024 | [13] | |
| Earth | 0.3307 | [14] | |
| Moon | 0.3929 ± 0.0009 | [15] | |
| Mars | 0.3644 ± 0.0005 | [16] | |
| Ceres | 0.36 ± 0.15[note 4] | [18] | Not measured (range reflects different assumptions for original spin rate[18]) |
| Jupiter | 0.2756 ± 0.0006 | [19] | Not measured (two-layer model calculations constrained by Juno gravity data[19]) |
| Io | 0.37824 ± 0.00022 | [20] | Not measured (Darwin-Radau relation) |
| Europa | 0.346 ± 0.005 | [20] | Not measured (Darwin-Radau relation) |
| Ganymede | 0.3115 ± 0.0028 | [20] | Not measured (Darwin-Radau relation) |
| Callisto | 0.3549 ± 0.0042 | [20] | Not measured (Darwin-Radau relation) |
| Saturn | 0.22 | [21] | Not measured (Darwin-Radau relation) |
| Enceladus | 0.3305 ± 0.0025 | [22] | Not measured (Darwin-Radau relation) |
| Rhea | 0.3911 ± 0.0045 | [23] | Not measured (Darwin-Radau relation) |
| Titan | 0.341 | [24] | Not measured (Darwin-Radau relation) |
| Uranus | 0.23 | [25] | Not measured (approximate solution to Clairaut's equation) |
| Neptune | 0.23 | [25] | Not measured (approximate solution to Clairaut's equation) |
Measurement[edit]
The polar moment of inertia is traditionally determined by combining measurements of spin quantities (spin precession rate and/or obliquity) with gravity quantities (coefficients of a spherical harmonic representation of the gravity field). These geodetic data usually require an orbiting spacecraft to collect.
Approximation[edit]
For bodies in hydrostatic equilibrium, the Darwin–Radau relation can provide estimates of the moment of inertia factor on the basis of shape, spin, and gravity quantities.[26]
Role in interior models[edit]
The moment of inertia factor provides an important constraint for models representing the interior structure of a planet or satellite. At a minimum, acceptable models of the density profile must match the volumetric mass density and moment of inertia factor of the body.
Gallery of internal structure models[edit]
-
The Sun (C/MR2 = 0.070)
-
Saturn (C/MR2 = 0.22)
-
Ganymede (C/MR2 = 0.3115)
-
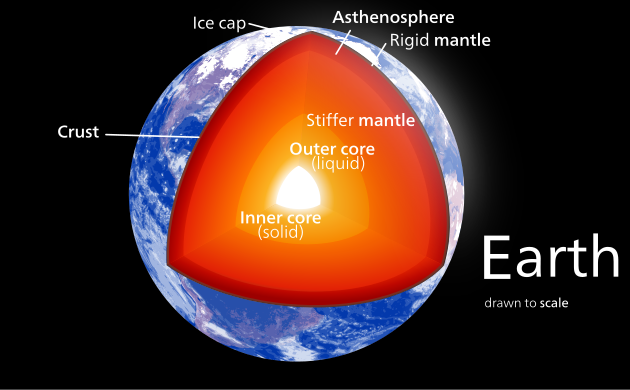
Earth (C/MR2 = 0.3307)
-
Callisto (C/MR2 = 0.3549)
-
The Moon (C/MR2 = 0.3929)
Notes[edit]
- ^ For a sphere with uniform density we can calculate the moment of inertia and the mass by integrating over disks from the "south pole" to the "north pole". Using a density of 1, a disk of radius r has a moment of inertia of
- ^ For several other examples (in which the rotation axis is the axis of symmetry if not otherwise specified), a solid cone has a factor of 3/10; a uniform thin rod (rotating about its center perpendicularly to its axis, so R is length/2) has a factor of 1/3; a hollow cone or a solid cylinder has a factor of 1/2; a hollow sphere has factor of 2/3; a hollow open-ended cylinder has a factor of 1.
- ^ A star's central density tends to increase over the course of its lifetime, aside from during brief core nuclear fusion ignition events like the helium flash.
- ^ The value given for Ceres is the mean moment of inertia, which is thought to better represent its interior structure than the polar moment of inertia, due to its high polar flattening.[17]
References[edit]
- ^ Hubbard, William B. (1984). Planetary interiors. New York, N.Y.: Van Nostrand Reinhold. ISBN 978-0442237042. OCLC 10147326.
- ^ de Pater, Imke; Lissauer, Jack J. (2015). Planetary sciences (2nd updated ed.). New York: Cambridge University Press. ISBN 978-0521853712. OCLC 903194732.
- ^ a b Williams, D. R. "Sun Fact Sheet". Planetary Fact Sheets. NASA. Retrieved 2017-01-26.
- ^ Robertson, Eugene C. (26 July 2001). "The Interior of the Earth". USGS. Retrieved 24 March 2007.
- ^ Hazlett, James S.; Monroe, Reed; Wicander, Richard (2006). Physical geology : exploring the earth (6. ed.). Belmont: Thomson. p. 346. ISBN 9780495011484.
- ^ Williams, David R. (7 September 2006). "Saturn Fact Sheet". NASA. Archived from the original on 14 April 2014. Retrieved 31 July 2007.
- ^ a b Showman, Adam P.; Malhotra, Renu (1999-10-01). "The Galilean Satellites" (PDF). Science. 286 (5437): 77–84. doi:10.1126/science.286.5437.77. PMID 10506564.
- ^ a b Sohl, F.; Spohn, T; Breuer, D.; Nagel, K. (2002). "Implications from Galileo Observations on the Interior Structure and Chemistry of the Galilean Satellites". Icarus. 157 (1): 104–119. Bibcode:2002Icar..157..104S. doi:10.1006/icar.2002.6828.
- ^ Showman, Adam P.; Stevenson, David J.; Malhotra, Renu (1997). "Coupled Orbital and Thermal Evolution of Ganymede" (PDF). Icarus. 129 (2): 367–383. Bibcode:1997Icar..129..367S. doi:10.1006/icar.1997.5778.
- ^ Brown, D.; Anderson, J. (6 January 2011). "NASA Research Team Reveals Moon Has Earth-Like Core". NASA. NASA.
- ^ Weber, R. C.; Lin, P.-Y.; Garnero, E. J.; Williams, Q.; Lognonne, P. (2011-01-21). "Seismic Detection of the Lunar Core" (PDF). Science. 331 (6015): 309–312. Bibcode:2011Sci...331..309W. doi:10.1126/science.1199375. PMID 21212323. S2CID 206530647. Archived from the original (PDF) on 2015-10-15. Retrieved 2017-04-10.
- ^ Margot, Jean-Luc; Peale, Stanton J.; Solomon, Sean C.; Hauck, Steven A.; Ghigo, Frank D.; Jurgens, Raymond F.; Yseboodt, Marie; Giorgini, Jon D.; Padovan, Sebastiano; Campbell, Donald B. (2012). "Mercury's moment of inertia from spin and gravity data". Journal of Geophysical Research: Planets. 117 (E12): E00L09–. Bibcode:2012JGRE..117.0L09M. doi:10.1029/2012JE004161. ISSN 0148-0227.
- ^ Margot, Jean-Luc; Campbell, Donald B.; Giorgini, Jon D.; Jao, Joseph S.; Snedeker, Lawrence G.; Ghigo, Frank D.; Bonsall, Amber (2021-04-29). "Spin state and moment of inertia of Venus". Nature Astronomy. 5 (7): 676–683. arXiv:2103.01504. Bibcode:2021NatAs...5..676M. doi:10.1038/s41550-021-01339-7. ISSN 2397-3366. S2CID 232092194.
- ^ Williams, James G. (1994). "Contributions to the Earth's obliquity rate, precession, and nutation". The Astronomical Journal. 108: 711. Bibcode:1994AJ....108..711W. doi:10.1086/117108. ISSN 0004-6256. S2CID 122370108.
- ^ Williams, James G.; Newhall, XX; Dickey, Jean O. (1996). "Lunar moments, tides, orientation, and coordinate frames". Planetary and Space Science. 44 (10): 1077–1080. Bibcode:1996P&SS...44.1077W. doi:10.1016/0032-0633(95)00154-9. ISSN 0032-0633.
- ^ Konopliv, Alex S.; Asmar, Sami W.; Folkner, William M.; Karatekin, Özgür; Nunes, Daniel C.; Smrekar, Suzanne E.; Yoder, Charles F.; Zuber, Maria T. (January 2011). "Mars high resolution gravity fields from MRO, Mars seasonal gravity, and other dynamical parameters". Icarus. 211 (1): 401–428. Bibcode:2011Icar..211..401K. doi:10.1016/j.icarus.2010.10.004.
- ^ Park, R. S.; Konopliv, A. S.; Bills, B. G.; Rambaux, N.; Castillo-Rogez, J. C.; Raymond, C. A.; Vaughan, A. T.; Ermakov, A. I.; Zuber, M. T.; Fu, R. R.; Toplis, M. J.; Russell, C. T.; Nathues, A.; Preusker, F. (2016-08-03). "A partially differentiated interior for (1) Ceres deduced from its gravity field and shape". Nature. 537 (7621): 515–517. Bibcode:2016Natur.537..515P. doi:10.1038/nature18955. PMID 27487219. S2CID 4459985.
- ^ a b Mao, X.; McKinnon, W. B. (2018). "Faster paleospin and deep-seated uncompensated mass as possible explanations for Ceres' present-day shape and gravity". Icarus. 299: 430–442. Bibcode:2018Icar..299..430M. doi:10.1016/j.icarus.2017.08.033.
- ^ a b Ni, D. (2018). "Empirical models of Jupiter's interior from Juno data". Astronomy & Astrophysics. 613: A32. doi:10.1051/0004-6361/201732183.
- ^ a b c d Schubert, G.; Anderson, J. D.; Spohn, T.; McKinnon, W. B. (2004). "Interior composition, structure and dynamics of the Galilean satellites". In Bagenal, F.; Dowling, T. E.; McKinnon, W. B. (eds.). Jupiter : the planet, satellites, and magnetosphere. New York: Cambridge University Press. pp. 281–306. ISBN 978-0521035453. OCLC 54081598.
- ^ Fortney, J.J.; Helled, R.; Nettlemann, N.; Stevenson, D.J.; Marley, M.S.; Hubbard, W.B.; Iess, L. (6 December 2018). "The Interior of Saturn". In Baines, K.H.; Flasar, F.M.; Krupp, N.; Stallard, T. (eds.). Saturn in the 21st Century. Cambridge University Press. pp. 44–68. ISBN 978-1-108-68393-7.
- ^ McKinnon, W. B. (2015). "Effect of Enceladus's rapid synchronous spin on interpretation of Cassini gravity". Geophysical Research Letters. 42 (7): 2137–2143. Bibcode:2015GeoRL..42.2137M. doi:10.1002/2015GL063384.
- ^ Anderson, J. D.; Schubert, G. (2007). "Saturn's satellite Rhea is a homogeneous mix of rock and ice". Geophysical Research Letters. 34 (2): L02202. Bibcode:2007GeoRL..34.2202A. doi:10.1029/2006GL028100. S2CID 128410558.
- ^ Durante, D.; Hemingway, D.J.; Racioppa, P.; Iess, L.; Stevenson, D.J. (2019). "Titan's gravity field and interior structure after Cassini" (PDF). Icarus. 326: 123–132. Bibcode:2019Icar..326..123D. doi:10.1016/j.icarus.2019.03.003. hdl:11573/1281269. S2CID 127984873.
- ^ a b Yoder, C. (1995). Ahrens, T. (ed.). Astrometric and Geodetic Properties of Earth and the Solar System. Washington, DC: AGU. ISBN 978-0-87590-851-9. OCLC 703657999. Archived from the original on 2016-03-04. Retrieved 2016-08-19.
- ^ Murray, Carl D.; Dermott, Stanley F. (13 February 2000). Solar System Dynamics. Cambridge: Cambridge University Press. ISBN 978-1139936156. OCLC 40857034.