Del in cylindrical and spherical coordinates

This is a list of some vector calculus formulae of general use in working with various curvilinear coordinate systems.

Note

• This page uses standard physics notation. For spherical coordinates, θ is the angle between the z axis and the radius vector connecting the origin to the point in question. ϕ is the angle between the projection of the radius vector onto the x-y plane and the x axis. Some sources reverse the definitions of θ and ϕ, so the meaning should be inferred from the context.
• The function atan2(y, x) can be used instead of the mathematical function arctan(y/x) due to its domain and image. The classical arctan(y/x) has an image of (-π/2, +π/2), whereas atan2(y, x) is defined to have an image of (-π, π]. (The expressions for the Del in spherical coordinates may need to be corrected)

Table with the del operator in cylindrical, spherical and parabolic cylindrical coordinates

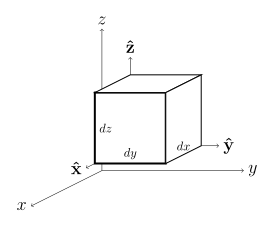
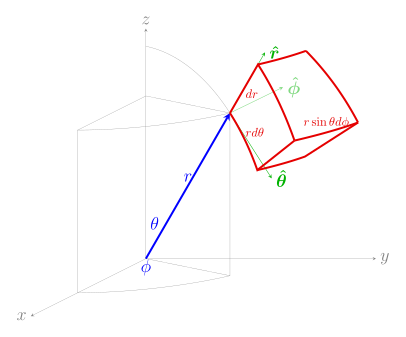
Operation	Cartesian coordinates (x,y,z)	Cylindrical coordinates (ρ,φ,z)	Spherical coordinates (r,θ,φ)	Parabolic cylindrical coordinates (σ,τ,z)
Definition of coordinates	$\begin{matrix} \rho & = & \sqrt{x^2+y^2} \\ \phi & = & \arctan(y/x) \\ z & = & z \end{matrix}$	$\begin{matrix} x & = & \rho\cos\phi \\ y & = & \rho\sin\phi \\ z & = & z \end{matrix}$	$\begin{matrix} x & = & r\sin\theta\cos\phi \\ y & = & r\sin\theta\sin\phi \\ z & = & r\cos\theta \end{matrix}$	$\begin{matrix} x & = & \sigma \tau\\ y & = & \frac{1}{2} \left( \tau^{2} - \sigma^{2} \right) \\ z & = & z \end{matrix}$
	$\begin{matrix} r & = & \sqrt{x^2+y^2+z^2} \\ \theta & = & \arccos(z/r)\\ \phi & = & \arctan(y/x) \\ \end{matrix}$	$\begin{matrix} r & = & \sqrt{\rho^2 + z^2} \\ \theta & = & \arctan{(\rho/z)}\\ \phi & = & \phi \end{matrix}$	$\begin{matrix} \rho & = & r\sin(\theta) \\ \phi & = & \phi\\ z & = & r\cos(\theta) \end{matrix}$	$\begin{matrix} \rho\cos\phi & = & \sigma \tau\\ \rho\sin\phi & = & \frac{1}{2} \left( \tau^{2} - \sigma^{2} \right) \\ z & = & z \end{matrix}$
Definition of unit vectors	$\begin{matrix} \boldsymbol{\hat \rho} & = & \frac{x}{\sqrt{x^2+y^2}}\mathbf{\hat x}+\frac{y}{\sqrt{x^2+y^2}}\mathbf{\hat y} \\ \boldsymbol{\hat\phi} & = & -\frac{y}{\sqrt{x^2+y^2}}\mathbf{\hat x}+\frac{x}{\sqrt{x^2+y^2}}\mathbf{\hat y} \\ \mathbf{\hat z} & = & \mathbf{\hat z} \end{matrix}$	$\begin{matrix} \mathbf{\hat x} & = & \cos\phi\boldsymbol{\hat \rho}-\sin\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat y} & = & \sin\phi\boldsymbol{\hat \rho}+\cos\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat z} & = & \mathbf{\hat z} \end{matrix}$	$\begin{matrix} \mathbf{\hat x} & = & \sin\theta\cos\phi\boldsymbol{\hat r}+\cos\theta\cos\phi\boldsymbol{\hat\theta}-\sin\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat y} & = & \sin\theta\sin\phi\boldsymbol{\hat r}+\cos\theta\sin\phi\boldsymbol{\hat\theta}+\cos\phi\boldsymbol{\hat\phi} \\ \mathbf{\hat z} & = & \cos\theta \boldsymbol{\hat r}-\sin\theta \boldsymbol{\hat\theta} \\ \end{matrix}$	$\begin{matrix} \boldsymbol{\hat \sigma} & = & \frac{\tau}{\sqrt{\tau^2+\sigma^2}}\mathbf{\hat x}-\frac{\sigma}{\sqrt{\tau^2+\sigma^2}}\mathbf{\hat y} \\ \boldsymbol{\hat\tau} & = & \frac{\sigma}{\sqrt{\tau^2+\sigma^2}}\mathbf{\hat x}+\frac{\tau}{\sqrt{\tau^2+\sigma^2}}\mathbf{\hat y} \\ \mathbf{\hat z} & = & \mathbf{\hat z} \end{matrix}$
	$\begin{matrix} \mathbf{\hat r} &=& \frac{ x }{\sqrt{x^2+y^2+z^2}}\mathbf{\hat x}\!+\!\frac{ y }{\sqrt{x^2+y^2+z^2}}\mathbf{\hat y}\!+\!\frac{z}{\sqrt{x^2+y^2+z^2}}\mathbf{\hat z}\\ \boldsymbol{\hat\theta} &=& \frac{ xz }{\sqrt{x^2+y^2+z^2}\sqrt{x^2+y^2}}\mathbf{\hat x}\!+\!\frac{ yz }{\sqrt{x^2+y^2+z^2}\sqrt{x^2+y^2}}\mathbf{\hat y}\!-\!\frac{\sqrt{x^2+y^2}}{\sqrt{x^2+y^2+z^2}}\mathbf{\hat z} \\ \boldsymbol{\hat\phi} &=& -\frac{y}{\sqrt{x^2+y^2}}\mathbf{\hat x}+\frac{x}{\sqrt{x^2+y^2}}\mathbf{\hat y} \end{matrix}$	$\begin{matrix} \mathbf{\hat r} & = & \frac{\rho}{\sqrt{\rho^2 +z^2}}\boldsymbol{\hat \rho}+\frac{ z}{\sqrt{\rho^2 +z^2}}\mathbf{\hat z} \\ \boldsymbol{\hat\theta} & = & \frac{z }{\sqrt{\rho^2 +z^2}}\boldsymbol{\hat \rho}-\frac{\rho}{\sqrt{\rho^2 +z^2}}\mathbf{\hat z} \\ \boldsymbol{\hat\phi} & = & \boldsymbol{\hat\phi} \end{matrix}$	$\begin{matrix} \boldsymbol{\hat \rho} & = & \sin\theta\mathbf{\hat r}+\cos\theta\boldsymbol{\hat\theta} \\ \boldsymbol{\hat\phi} & = & \boldsymbol{\hat\phi} \\ \mathbf{\hat z} & = & \cos\theta\mathbf{\hat r}-\sin\theta\boldsymbol{\hat\theta} \\ \end{matrix}$	$\begin{matrix} \end{matrix}$
A vector field $\mathbf{A}$	$A_x\mathbf{\hat x} + A_y\mathbf{\hat y} + A_z\mathbf{\hat z}$	$A_\rho\boldsymbol{\hat \rho} + A_\phi\boldsymbol{\hat \phi} + A_z\boldsymbol{\hat z}$	$A_r\boldsymbol{\hat r} + A_\theta\boldsymbol{\hat \theta} + A_\phi\boldsymbol{\hat \phi}$	$A_\sigma\boldsymbol{\hat \sigma} + A_\tau\boldsymbol{\hat \tau} + A_\phi\boldsymbol{\hat z}$
Gradient $\nabla f$	${\partial f \over \partial x}\mathbf{\hat x} + {\partial f \over \partial y}\mathbf{\hat y} + {\partial f \over \partial z}\mathbf{\hat z}$	${\partial f \over \partial \rho}\boldsymbol{\hat \rho} + {1 \over \rho}{\partial f \over \partial \phi}\boldsymbol{\hat \phi} + {\partial f \over \partial z}\boldsymbol{\hat z}$	${\partial f \over \partial r}\boldsymbol{\hat r} + {1 \over r}{\partial f \over \partial \theta}\boldsymbol{\hat \theta} + {1 \over r\sin\theta}{\partial f \over \partial \phi}\boldsymbol{\hat \phi}$	$\frac{1}{\sqrt{\sigma^{2} + \tau^{2}}} {\partial f \over \partial \sigma}\boldsymbol{\hat \sigma} + \frac{1}{\sqrt{\sigma^{2} + \tau^{2}}} {\partial f \over \partial \tau}\boldsymbol{\hat \tau} + {\partial f \over \partial z}\boldsymbol{\hat z}$
Divergence $\nabla \cdot \mathbf{A}$	${\partial A_x \over \partial x} + {\partial A_y \over \partial y} + {\partial A_z \over \partial z}$	${1 \over \rho}{\partial \left( \rho A_\rho \right) \over \partial \rho} + {1 \over \rho}{\partial A_\phi \over \partial \phi} + {\partial A_z \over \partial z}$	${1 \over r^2}{\partial \left( r^2 A_r \right) \over \partial r} + {1 \over r\sin\theta}{\partial \over \partial \theta} \left( A_\theta\sin\theta \right) + {1 \over r\sin\theta}{\partial A_\phi \over \partial \phi}$	$\frac{1}{\sigma^{2} + \tau^{2}}{\partial A_\sigma \over \partial \sigma} + \frac{1}{\sigma^{2} + \tau^{2}}{\partial A_\tau \over \partial \tau} + {\partial A_z \over \partial z}$
Curl $\nabla \times \mathbf{A}$	$\begin{matrix} \displaystyle\left({\partial A_z \over \partial y} - {\partial A_y \over \partial z}\right) \mathbf{\hat x} & + \\ \displaystyle\left({\partial A_x \over \partial z} - {\partial A_z \over \partial x}\right) \mathbf{\hat y} & + \\ \displaystyle\left({\partial A_y \over \partial x} - {\partial A_x \over \partial y}\right) \mathbf{\hat z} & \ \end{matrix}$	$\begin{matrix} \displaystyle\left({1 \over \rho}{\partial A_z \over \partial \phi} - {\partial A_\phi \over \partial z}\right) \boldsymbol{\hat \rho} & + \\ \displaystyle\left({\partial A_\rho \over \partial z} - {\partial A_z \over \partial \rho}\right) \boldsymbol{\hat \phi} & + \\ \displaystyle{1 \over \rho}\left({\partial \left( \rho A_\phi \right) \over \partial \rho} - {\partial A_\rho \over \partial \phi}\right) \boldsymbol{\hat z} & \ \end{matrix}$	$\begin{matrix} \displaystyle{1 \over r\sin\theta}\left({\partial \over \partial \theta} \left( A_\phi\sin\theta \right) - {\partial A_\theta \over \partial \phi}\right) \boldsymbol{\hat r} & + \\ \displaystyle{1 \over r}\left({1 \over \sin\theta}{\partial A_r \over \partial \phi} - {\partial \over \partial r} \left( r A_\phi \right) \right) \boldsymbol{\hat \theta} & + \\ \displaystyle{1 \over r}\left({\partial \over \partial r} \left( r A_\theta \right) - {\partial A_r \over \partial \theta}\right) \boldsymbol{\hat \phi} & \ \end{matrix}$	$\begin{matrix} \displaystyle\left(\frac{1}{\sqrt{\sigma^{2} + \tau^{2}}}{\partial A_z \over \partial \tau} - {\partial A_\tau \over \partial z}\right) \boldsymbol{\hat \sigma} & - \\ \displaystyle\left(\frac{1}{\sqrt{\sigma^{2} + \tau^{2}}}{\partial A_z \over \partial \sigma}- {\partial A_\sigma \over \partial z}\right) \boldsymbol{\hat \tau} & + \\ \displaystyle\frac{1}{\sqrt{\sigma^{2} + \tau^{2}}}\left({\partial \left( \sqrt{\sigma^{2} + \tau^{2}} A_\sigma \right) \over \partial \tau} - {\partial \left( \sqrt{\sigma^{2} + \tau^{2}} A_\tau \right) \over \partial \sigma}\right) \boldsymbol{\hat z} & \ \end{matrix}$
Laplace operator $\Delta f = \nabla^2 f$	${\partial^2 f \over \partial x^2} + {\partial^2 f \over \partial y^2} + {\partial^2 f \over \partial z^2}$	${1 \over \rho}{\partial \over \partial \rho}\left(\rho {\partial f \over \partial \rho}\right) + {1 \over \rho^2}{\partial^2 f \over \partial \phi^2} + {\partial^2 f \over \partial z^2}$	${1 \over r^2}{\partial \over \partial r}\!\left(r^2 {\partial f \over \partial r}\right) \!+\!{1 \over r^2\!\sin\theta}{\partial \over \partial \theta}\!\left(\sin\theta {\partial f \over \partial \theta}\right) \!+\!{1 \over r^2\!\sin^2\theta}{\partial^2 f \over \partial \phi^2}$	$\frac{1}{\sigma^{2} + \tau^{2}} \left( \frac{\partial^{2} f}{\partial \sigma^{2}} + \frac{\partial^{2} f}{\partial \tau^{2}} \right) + \frac{\partial^{2} f}{\partial z^{2}}$
Vector Laplacian $\Delta \mathbf{A} = \nabla^2 \mathbf{A}$	$\Delta A_x \mathbf{\hat x} + \Delta A_y \mathbf{\hat y} + \Delta A_z \mathbf{\hat z}$	$\begin{matrix} \displaystyle\left(\Delta A_\rho - {A_\rho \over \rho^2} - {2 \over \rho^2}{\partial A_\phi \over \partial \phi}\right) \boldsymbol{\hat \rho} & + \\ \displaystyle\left(\Delta A_\phi - {A_\phi \over \rho^2} + {2 \over \rho^2}{\partial A_\rho \over \partial \phi}\right) \boldsymbol{\hat\phi} & + \\ \displaystyle\left(\Delta A_z \right) \boldsymbol{\hat z} & \ \end{matrix}$	$\begin{matrix} \left(\Delta A_r - {2 A_r \over r^2} - {2 \over r^2\sin\theta}{\partial \left(A_\theta \sin\theta\right) \over \partial\theta} - {2 \over r^2\sin\theta}{\partial A_\phi \over \partial \phi}\right) \boldsymbol{\hat r} & + \\ \left(\Delta A_\theta - {A_\theta \over r^2\sin^2\theta} + {2 \over r^2}{\partial A_r \over \partial \theta} - {2 \cos\theta \over r^2\sin^2\theta}{\partial A_\phi \over \partial \phi}\right) \boldsymbol{\hat\theta} & + \\ \left(\Delta A_\phi - {A_\phi \over r^2\sin^2\theta} + {2 \over r^2\sin\theta}{\partial A_r \over \partial \phi} + {2 \cos\theta \over r^2\sin^2\theta}{\partial A_\theta \over \partial \phi}\right) \boldsymbol{\hat\phi} & \end{matrix}$
Material derivative $(\mathbf{A} \cdot \nabla) \mathbf{B}$	$\begin{matrix} \displaystyle\left(A_x \frac{\partial B_x}{\partial x}+A_y \frac{\partial B_x}{\partial y} + A_z \frac{\partial B_x}{\partial z}\right)\boldsymbol{\hat{x}} & + \\ \displaystyle\left(A_x \frac{\partial B_y}{\partial x}+A_y \frac{\partial B_y}{\partial y} + A_z \frac{\partial B_y}{\partial z}\right)\boldsymbol{\hat{y}} & + \\ \displaystyle\left(A_x \frac{\partial B_z}{\partial x}+A_y \frac{\partial B_z}{\partial y} + A_z \frac{\partial B_z}{\partial z}\right)\boldsymbol{\hat{z}} \end{matrix}$	$\begin{matrix} \left(A_\rho \frac{\partial B_\rho}{\partial \rho}+\frac{A_\phi}{\rho}\frac{\partial B_\rho}{\partial \phi}+A_z\frac{\partial B_\rho}{\partial z}-\frac{A_\phi B_\phi}{\rho}\right) \boldsymbol{\hat\rho} \!+\!\\ \left(A_\rho \frac{\partial B_\phi}{\partial \rho}+\frac{A_\phi}{\rho}\frac{\partial B_\phi}{\partial \phi}+A_z\frac{\partial B_\phi}{\partial z}+\frac{A_\phi B_\rho}{\rho}\right) \boldsymbol{\hat\phi}\!+\!\\ \left(A_\rho \frac{\partial B_z }{\partial \rho}+\frac{A_\phi}{\rho}\frac{\partial B_z }{\partial \phi}+A_z\frac{\partial B_z }{\partial z} \right) \boldsymbol{\hat z} \end{matrix}$	$\begin{matrix} \left(A_r \frac{\partial B_r}{\partial r}\!+\!\frac{A_\theta}{r}\frac{\partial B_r}{\partial \theta}\!+\!\frac{A_\phi}{r\sin(\theta)}\frac{\partial B_r}{\partial \phi}\!-\!\frac{A_\theta B_\theta\!+\!A_\phi B_\phi}{r}\right) \boldsymbol{\hat r} \!+\!\\ \left(A_r \frac{\partial B_\theta}{\partial r}\!+\!\frac{A_\theta}{r}\frac{\partial B_\theta}{\partial \theta}\!+\!\frac{A_\phi}{r\sin(\theta)}\frac{\partial B_\theta}{\partial \phi}\!+\!\frac{A_\theta B_r}{r}-\frac{A_\phi B_\phi\cot(\theta)}{r}\right) \boldsymbol{\hat\theta} \!+\!\\ \left(A_r \frac{\partial B_\phi}{\partial r}\!+\!\frac{A_\theta}{r}\frac{\partial B_\phi}{\partial \theta}\!+\!\frac{A_\phi}{r\sin(\theta)}\frac{\partial B_\phi}{\partial \phi}\!+\!\frac{A_\phi B_r}{r}\!+\!\frac{A_\phi B_\theta \cot(\theta)}{r}\right)\boldsymbol{\hat\phi} \end{matrix}$
Differential displacement	$d\mathbf{l} = dx\mathbf{\hat x} + dy\mathbf{\hat y} + dz\mathbf{\hat z}$	$d\mathbf{l} = d\rho\boldsymbol{\hat \rho} + \rho d\phi\boldsymbol{\hat \phi} + dz\boldsymbol{\hat z}$	$d\mathbf{l} = dr\mathbf{\hat r} + rd\theta\boldsymbol{\hat \theta} + r\sin\theta d\phi\boldsymbol{\hat \phi}$	$d\mathbf{l} = \sqrt{\sigma^{2} + \tau^{2}} d\sigma\boldsymbol{\hat \sigma} + \sqrt{\sigma^{2} + \tau^{2}} d\tau\boldsymbol{\hat \tau} + dz\boldsymbol{\hat z}$
Differential normal area	$\begin{matrix}d\mathbf{S} = &dy\,dz\,\mathbf{\hat x} + \\ &dx\,dz\,\mathbf{\hat y} + \\ &dx\,dy\,\mathbf{\hat z}\end{matrix}$	$\begin{matrix} d\mathbf{S} = & \rho\, d\phi\, dz\,\boldsymbol{\hat \rho} + \\ & d\rho \,dz\,\boldsymbol{\hat \phi} + \\ & \rho \,d\rho d\phi \,\mathbf{\hat z} \end{matrix}$	$\begin{matrix} d\mathbf{S} = & r^2 \sin\theta \,d\theta \,d\phi \,\mathbf{\hat r} + \\ & r\sin\theta \,dr\,d\phi \,\boldsymbol{\hat \theta} + \\ & r\,dr\,d\theta\,\boldsymbol{\hat \phi} \end{matrix}$	$\begin{matrix} d\mathbf{S} = & \sqrt{\sigma^{2} + \tau^{2}}, d\tau\, dz\,\boldsymbol{\hat \sigma} + \\ & \sqrt{\sigma^{2} + \tau^{2}} d\sigma\,dz\,\boldsymbol{\hat \tau} + \\ & \sigma^{2} + \tau^{2} d\sigma, d\tau \,\mathbf{\hat z} \end{matrix}$
Differential volume	$dV = dx\,dy\,dz \,$	$dV = \rho\, d\rho\, d\phi\, dz\,$	$dV = r^2\sin\theta \,dr\,d\theta\, d\phi\,$	$dV = \left( \sigma^{2} + \tau^{2} \right) d\sigma d\tau dz,$
Non-trivial calculation rules: $\operatorname{div\ grad\ } f = \nabla \cdot (\nabla f) = \nabla^2 f = \Delta f$ (Laplacian) $\operatorname{curl\ grad\ } f = \nabla \times (\nabla f) = \mathbf{0}$ $\operatorname{div\ curl\ } \mathbf{A} = \nabla \cdot (\nabla \times \mathbf{A}) = 0$ $\operatorname{curl\ curl\ } \mathbf{A} = \nabla \times (\nabla \times \mathbf{A}) = \nabla (\nabla \cdot \mathbf{A}) - \nabla^2 \mathbf{A}$ (using Lagrange's formula for the cross product) $\Delta f g = f \Delta g + 2 \nabla f \cdot \nabla g + g \Delta f$

See also

• Del
• Orthogonal coordinates
• Curvilinear coordinates
• Vector fields in cylindrical and spherical coordinates

External links

• Maxima Computer Algebra system scripts to generate some of these operators in cylindrical and spherical coordinates.