Directional derivative

In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V. It therefore generalizes the notion of a partial derivative, in which the direction is always taken parallel to one of the coordinate axes.

The directional derivative is a special case of the Gâteaux derivative.

Definition

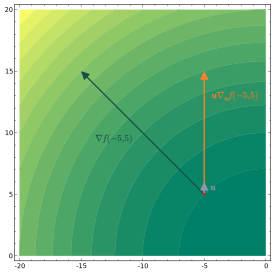
The directional derivative of a scalar function

$f(\vec{x}) = f(x_1, x_2, \ldots, x_n)$

along a unit vector

$\vec{u} = (u_1, \ldots, u_n)$

is the function defined by the limit

$\nabla_{\vec{u}}{f}(\vec{x}) = \lim_{h \rightarrow 0^+}{\frac{f(\vec{x} + h\vec{u}) - f(\vec{x})}{h}}.$

(See other notations below.) If the function f is differentiable at $\vec{x}$, then the directional derivative exists along any unit vector $\vec{u},$ and one has

$\nabla_{\vec{u}}{f}(\vec{x}) = \nabla f(\vec{x}) \cdot \vec{u}$

where the $\nabla$ on the right denotes the gradient and $\cdot$ is the Euclidean inner product. At any point $\vec{x}$, the directional derivative of f intuitively represents the rate of change in f along $\vec{u}$ at the point $\vec{x}$.

One sometimes permits non-unit vectors, allowing the directional derivative to be taken in the direction of $\vec{v}$, where $\vec{v}$ is any nonzero vector. In this case, one must modify the definitions to account for the fact that $\vec{v}$ may not be normalized, so one has

$\nabla_{\vec{v}}{f}(\vec{x}) = \lim_{h \rightarrow 0^+}{\frac{f(\vec{x} + h\vec{v}) - f(\vec{x})}{h|\vec{v}|}},$

or in case f is differentiable at $\vec{x}$,

$\nabla_{\vec{v}}{f}(\vec{x}) = \nabla f(\vec{x}) \cdot \frac{\vec{v}}{|\vec{v}|}$

Such notation for non-unit vectors (undefined for the zero vector), however, is incompatible with notation used elsewhere in mathematics, where the space of derivations in a derivation algebra is expected to be a vector space.

Notation

Directional derivatives can be also denoted by:

$\nabla_{\vec{u}}{f}(\vec{x}) \sim \frac{\partial{f(\vec{x})}}{\partial{u}} \sim f'_\mathbf{u}(\mathbf{x}) \sim D_\mathbf{u}f(\mathbf{x}) \sim \mathbf{u}\cdot{\nabla f(\mathbf{x})}$

Properties

Many of the familiar properties of the ordinary derivative hold for the directional derivative. These include, for any functions f and g defined in a neighborhood of, and differentiable at, p:

• The sum rule: $\nabla_v (f + g) = \nabla_v f + \nabla_v g$
• The constant factor rule: For any constant c, $\nabla_v (cf) = c\nabla_v f$
• The product rule (or Leibniz rule): $\nabla_v (fg) = g\nabla_v f + f\nabla_v g$
• The chain rule: If g is differentiable at p and h is differentiable at g(p), then

$\nabla_v h\circ g (p) = h'(g(p)) \nabla_v g (p)$

In differential geometry

See also: Tangent space#Tangent vectors as directional derivatives

Let M be a differentiable manifold and p a point of M. Suppose that f is a function defined in a neighborhood of p, and differentiable at p. If v is a tangent vector to M at p, then the directional derivative of f along v, denoted variously as $\nabla_v f(p)$ (see covariant derivative), L_vf(p) (see Lie derivative), or v_p(f) (see Tangent space#Definition via derivations), can be defined as follows. Let γ : [-1,1] → M be a differentiable curve with γ(0) = p and γ′(0) = v. Then the directional derivative is defined by

$\nabla_v f(p) = \left.\frac{d}{d\tau} f\circ\gamma(\tau)\right|_{\tau=0}$

This definition can be proven independent of the choice of γ, provided γ is selected in the prescribed manner so that γ′(0) = v.

Normal derivative

A normal derivative is a directional derivative taken in the direction normal (that is, orthogonal) to some surface in space, or more generally along a normal vector field orthogonal to some hypersurface. See for example Neumann boundary condition. If the normal direction is denoted by $\vec{n}$, then the directional derivative of a function ƒ is sometimes denoted as $\frac{ \partial f}{\partial n}$. In other notations

$\frac{ \partial f}{\partial n} = \nabla f(\vec{x}) \cdot \vec{n} = \nabla_{\vec{n}}{f}(\vec{x}) = \frac{\partial f}{\partial \vec{x}}\cdot\vec{n} = Df(\vec{x})[\vec{n}]$

In the continuum mechanics of solids

Several important results in continuum mechanics require the derivatives of vectors with respect to vectors and of tensors with respect to vectors and tensors. The directional directive provides a systematic way of finding these derivatives.

The definitions of directional derivatives for various situations are given below. It is assumed that the functions are sufficiently smooth that derivatives can be taken.

Derivatives of scalar valued functions of vectors

Let $f(\mathbf{v})$ be a real valued function of the vector $\mathbf{v}$. Then the derivative of $f(\mathbf{v})$ with respect to $\mathbf{v}$ (or at $\mathbf{v}$) in the direction $\mathbf{u}$ is the vector defined as

$\frac{\partial f}{\partial \mathbf{v}}\cdot\mathbf{u} = Df(\mathbf{v})[\mathbf{u}] = \left[\frac{d }{d \alpha}~f(\mathbf{v} + \alpha~\mathbf{u})\right]_{\alpha = 0}$

for all vectors $\mathbf{u}$.

Properties:

1) If $f(\mathbf{v}) = f_1(\mathbf{v}) + f_2(\mathbf{v})$ then $\frac{\partial f}{\partial \mathbf{v}}\cdot\mathbf{u} = \left(\frac{\partial f_1}{\partial \mathbf{v}} + \frac{\partial f_2}{\partial \mathbf{v}}\right)\cdot\mathbf{u}$

2) If $f(\mathbf{v}) = f_1(\mathbf{v})~ f_2(\mathbf{v})$ then $\frac{\partial f}{\partial \mathbf{v}}\cdot\mathbf{u} = \left(\frac{\partial f_1}{\partial \mathbf{v}}\cdot\mathbf{u}\right)~f_2(\mathbf{v}) + f_1(\mathbf{v})~\left(\frac{\partial f_2}{\partial \mathbf{v}}\cdot\mathbf{u} \right)$

3) If $f(\mathbf{v}) = f_1(f_2(\mathbf{v}))$ then $\frac{\partial f}{\partial \mathbf{v}}\cdot\mathbf{u} = \frac{\partial f_1}{\partial f_2}~\frac{\partial f_2}{\partial \mathbf{v}}\cdot\mathbf{u}$

Derivatives of vector valued functions of vectors

Let $\mathbf{f}(\mathbf{v})$ be a vector valued function of the vector $\mathbf{v}$. Then the derivative of $\mathbf{f}(\mathbf{v})$ with respect to $\mathbf{v}$ (or at $\mathbf{v}$) in the direction $\mathbf{u}$ is the second order tensor defined as

$\frac{\partial \mathbf{f}}{\partial \mathbf{v}}\cdot\mathbf{u} = D\mathbf{f}(\mathbf{v})[\mathbf{u}] = \left[\frac{d }{d \alpha}~\mathbf{f}(\mathbf{v} + \alpha~\mathbf{u})\right]_{\alpha = 0}$

for all vectors $\mathbf{u}$.

Properties:

1) If $\mathbf{f}(\mathbf{v}) = \mathbf{f}_1(\mathbf{v}) + \mathbf{f}_2(\mathbf{v})$ then $\frac{\partial \mathbf{f}}{\partial \mathbf{v}}\cdot\mathbf{u} = \left(\frac{\partial \mathbf{f}_1}{\partial \mathbf{v}} + \frac{\partial \mathbf{f}_2}{\partial \mathbf{v}}\right)\cdot\mathbf{u}$

2) If $\mathbf{f}(\mathbf{v}) = \mathbf{f}_1(\mathbf{v})\times\mathbf{f}_2(\mathbf{v})$ then $\frac{\partial \mathbf{f}}{\partial \mathbf{v}}\cdot\mathbf{u} = \left(\frac{\partial \mathbf{f}_1}{\partial \mathbf{v}}\cdot\mathbf{u}\right)\times\mathbf{f}_2(\mathbf{v}) + \mathbf{f}_1(\mathbf{v})\times\left(\frac{\partial \mathbf{f}_2}{\partial \mathbf{v}}\cdot\mathbf{u} \right)$

3) If $\mathbf{f}(\mathbf{v}) = \mathbf{f}_1(\mathbf{f}_2(\mathbf{v}))$ then $\frac{\partial \mathbf{f}}{\partial \mathbf{v}}\cdot\mathbf{u} = \frac{\partial \mathbf{f}_1}{\partial \mathbf{f}_2}\cdot\left(\frac{\partial \mathbf{f}_2}{\partial \mathbf{v}}\cdot\mathbf{u} \right)$

Derivatives of scalar valued functions of second-order tensors

Let $f(\boldsymbol{S})$ be a real valued function of the second order tensor $\boldsymbol{S}$. Then the derivative of $f(\boldsymbol{S})$ with respect to $\boldsymbol{S}$ (or at $\boldsymbol{S}$) in the direction $\boldsymbol{T}$ is the second order tensor defined as

$\frac{\partial f}{\partial \boldsymbol{S}}:\boldsymbol{T} = Df(\boldsymbol{S})[\boldsymbol{T}] = \left[\frac{d }{d \alpha}~f(\boldsymbol{S} + \alpha~\boldsymbol{T})\right]_{\alpha = 0}$

for all second order tensors $\boldsymbol{T}$.

Properties:

1) If $f(\boldsymbol{S}) = f_1(\boldsymbol{S}) + f_2(\boldsymbol{S})$ then $\frac{\partial f}{\partial \boldsymbol{S}}:\boldsymbol{T} = \left(\frac{\partial f_1}{\partial \boldsymbol{S}} + \frac{\partial f_2}{\partial \boldsymbol{S}}\right):\boldsymbol{T}$

2) If $f(\boldsymbol{S}) = f_1(\boldsymbol{S})~ f_2(\boldsymbol{S})$ then $\frac{\partial f}{\partial \boldsymbol{S}}:\boldsymbol{T} = \left(\frac{\partial f_1}{\partial \boldsymbol{S}}:\boldsymbol{T}\right)~f_2(\boldsymbol{S}) + f_1(\boldsymbol{S})~\left(\frac{\partial f_2}{\partial \boldsymbol{S}}:\boldsymbol{T} \right)$

3) If $f(\boldsymbol{S}) = f_1(f_2(\boldsymbol{S}))$ then $\frac{\partial f}{\partial \boldsymbol{S}}:\boldsymbol{T} = \frac{\partial f_1}{\partial f_2}~\left(\frac{\partial f_2}{\partial \boldsymbol{S}}:\boldsymbol{T} \right)$

Derivatives of tensor valued functions of second-order tensors

Let $\boldsymbol{F}(\boldsymbol{S})$ be a second order tensor valued function of the second order tensor $\boldsymbol{S}$. Then the derivative of $\boldsymbol{F}(\boldsymbol{S})$ with respect to $\boldsymbol{S}$ (or at $\boldsymbol{S}$) in the direction $\boldsymbol{T}$ is the fourth order tensor defined as

$\frac{\partial \boldsymbol{F}}{\partial \boldsymbol{S}}:\boldsymbol{T} = D\boldsymbol{F}(\boldsymbol{S})[\boldsymbol{T}] = \left[\frac{d }{d \alpha}~\boldsymbol{F}(\boldsymbol{S} + \alpha~\boldsymbol{T})\right]_{\alpha = 0}$

for all second order tensors $\boldsymbol{T}$.

Properties:

1) If $\boldsymbol{F}(\boldsymbol{S}) = \boldsymbol{F}_1(\boldsymbol{S}) + \boldsymbol{F}_2(\boldsymbol{S})$ then $\frac{\partial \boldsymbol{F}}{\partial \boldsymbol{S}}:\boldsymbol{T} = \left(\frac{\partial \boldsymbol{F}_1}{\partial \boldsymbol{S}} + \frac{\partial \boldsymbol{F}_2}{\partial \boldsymbol{S}}\right):\boldsymbol{T}$

2) If $\boldsymbol{F}(\boldsymbol{S}) = \boldsymbol{F}_1(\boldsymbol{S})\cdot\boldsymbol{F}_2(\boldsymbol{S})$ then $\frac{\partial \boldsymbol{F}}{\partial \boldsymbol{S}}:\boldsymbol{T} = \left(\frac{\partial \boldsymbol{F}_1}{\partial \boldsymbol{S}}:\boldsymbol{T}\right)\cdot\boldsymbol{F}_2(\boldsymbol{S}) + \boldsymbol{F}_1(\boldsymbol{S})\cdot\left(\frac{\partial \boldsymbol{F}_2}{\partial \boldsymbol{S}}:\boldsymbol{T} \right)$

3) If $\boldsymbol{F}(\boldsymbol{S}) = \boldsymbol{F}_1(\boldsymbol{F}_2(\boldsymbol{S}))$ then $\frac{\partial \boldsymbol{F}}{\partial \boldsymbol{S}}:\boldsymbol{T} = \frac{\partial \boldsymbol{F}_1}{\partial \boldsymbol{F}_2}:\left(\frac{\partial \boldsymbol{F}_2}{\partial \boldsymbol{S}}:\boldsymbol{T} \right)$

4) If $f(\boldsymbol{S}) = f_1(\boldsymbol{F}_2(\boldsymbol{S}))$ then $\frac{\partial f}{\partial \boldsymbol{S}}:\boldsymbol{T} = \frac{\partial f_1}{\partial \boldsymbol{F}_2}:\left(\frac{\partial \boldsymbol{F}_2}{\partial \boldsymbol{S}}:\boldsymbol{T} \right)$

References

Hildebrand, F. B. (1976). Advanced Calculus for Applications. Prentice Hall. ISBN 0130111899. 

See also

• Fréchet derivative
• Gâteaux derivative
• Derivative (generalizations)
• Lie derivative
• Differential form
• Structure tensor
• Tensor derivative (continuum mechanics)
• Del in cylindrical and spherical coordinates

External links

• Directional derivatives at MathWorld
• Directional derivative at PlanetMath