OpenMx
 | |
| Paradigm | Structural Equation Modeling |
|---|---|
| Designed by | OpenMx Team |
| Developer | The OpenMx Development Core Team |
| First appeared | 2010 [1] |
| Stable release | 2.19.8 [2]
/ September 24, 2021 |
| Preview release | Beta
/ July 19, 2017 |
| Typing discipline | Dynamic |
| OS | Cross-platform |
| License | Apache License, Version 2.0 |
| Website | openmx.ssri.psu.edu |
| Influenced by | |
| Mx, R | |
| Influenced | |
| metaSEM; simsem and semTools, Onyx, umx helper library | |
OpenMx is an open source program for extended structural equation modeling. It runs as a package under R. Cross platform, it runs under Linux, Mac OS and Windows.[2]
Overview
[edit]OpenMx consists of an R library of functions and optimizers supporting the rapid and flexible implementation and estimation of SEM models. Models can be estimated based on either raw data (with FIML modelling) or on correlation or covariance matrices. Models can handle mixtures of continuous and ordinal data. The current version is OpenMx 2,[3] and is available on CRAN.
Path analysis, Confirmatory factor analysis, Latent growth modeling, Mediation analysis are all implemented. Multiple group models are implemented readily. When a model is run, it returns a model, and models can be updated (adding and removing paths, adding constraints and equalities; giving parameters the same label equates them). An innovation is that labels can consist of address of other parameters, allowing easy implementation of constraints on parameters by address.
RAM models return standardized and raw estimates, as well as a range of fit indices (AIC, RMSEA, TLI, CFI etc.). Confidence intervals are estimated robustly.
The program has parallel processing built-in via links to parallel environments in R, and in general takes advantage of the R programming environment.
Users can expand the package with functions. These have been used, for instance, to implement Modification indices.
Models can be written in either a "pathic" or "matrix" form. For those who think in terms of path models, paths are specified using mxPath() to describe paths. For models that are better suited to description in terms of matrix algebra, this is done using similar functional extensions in the R environment, for instance mxMatrix and mxAlgebra.
The code below shows how to implement a simple Confirmatory factor analysis in OpenMx, using either path or matrix formats. The model is diagrammed here:
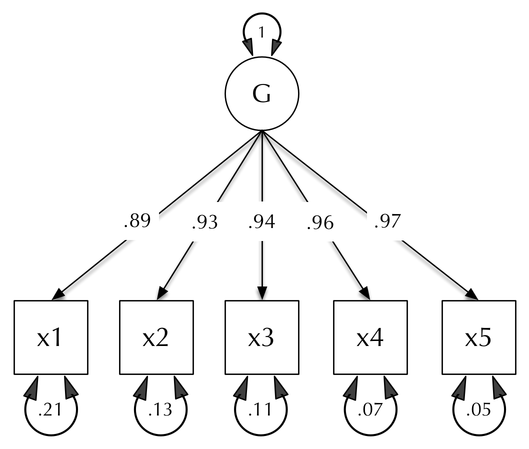
Example path model specification
[edit]Below is the code to implement, run, and print a summary for estimating a one-factor path model with five indicators.
require(OpenMx)
data(demoOneFactor)
manifests <- names(demoOneFactor)
latents <- c("G")
m1 <- mxModel("One Factor", type="RAM",
manifestVars = manifests,
latentVars = latents,
mxPath(from=latents, to=manifests),
mxPath(from=manifests, arrows=2),
mxPath(from=latents, arrows=2, free=FALSE, values=1.0),
mxData(cov(demoOneFactor), type="cov", numObs=500)
)
summary(mxRun(m1))
Example matrix specification
[edit]Below is the code to implement, run, and print a summary for estimating a one-factor path model with five indicators.
library(OpenMx)
data(demoOneFactor)
df = cov(demoOneFactor)
m1 <- mxModel("One Factor",
mxMatrix("Full", nrow = 5, ncol = 1, values = 0.2, free = TRUE, name = "A"),
mxMatrix("Symm", nrow = 1, ncol = 1, values = 1.0, free = FALSE, name = "L"),
mxMatrix("Diag", nrow = 5, ncol = 5, values = 1.0, free = TRUE, name = "U"),
mxAlgebra(A %*% L %*% t(A) + U, name="R"),
mxExpectationNormal(covariance= "R", dimnames = names(demoOneFactor)),
mxFitFunctionML(),
mxData(df, type = "cov", numObs=500)
)
summary(mxRun(m1))
References
[edit]- ^ Release 1.0 Announcing OpenMx 1, The OpenMx Development Team, available from the OpenMx website
- ^ S. Boker, M. Neale, H. Maes, M. Wilde, M. Spiegel, T. Brick, J. Spies, R. Estabrook, S. Kenny, T. Bates, P. Mehta and J. Fox. (2011). OpenMx: An Open Source Extended Structural Equation Modeling Framework. Psychometrika, 76, [1]
- ^ Neale, Michael C.; Hunter, Michael D.; Pritikin, Joshua N.; Zahery, Mahsa; Brick, Timothy R.; Kirkpatrick, Robert M.; Estabrook, Ryne; Bates, Timothy C.; Maes, Hermine H.; Boker, Steven M. (2015). "OpenMx 2.0: Extended Structural Equation and Statistical Modeling". Psychometrika. 81 (2): 535–549. doi:10.1007/s11336-014-9435-8. ISSN 0033-3123. PMC 4516707. PMID 25622929.
