Mathematical model of a thin, flat object
In mathematics , a planar lamina (or plane lamina [1] integration .
Planar laminas can be used to determine moments of inertia , or center of mass of flat figures, as well as an aid in corresponding calculations for 3D bodies.
Definition [ edit ] Basically, a planar lamina is defined as a figure (a closed set ) D of a finite area in a plane, with some mass m .[2]
This is useful in calculating moments of inertia or center of mass for a constant density, because the mass of a lamina is proportional to its area. In a case of a variable density, given by some (non-negative) surface density function
ρ
(
x
,
y
)
,
{\displaystyle \rho (x,y),}
m
{\displaystyle m}
D is a planar integral of ρ over the figure:[3]
m
=
∬
D
ρ
(
x
,
y
)
d
x
d
y
{\displaystyle m=\iint _{D}\rho (x,y)\,dx\,dy}
Properties [ edit ] The center of mass of the lamina is at the point
(
M
y
m
,
M
x
m
)
{\displaystyle \left({\frac {M_{y}}{m}},{\frac {M_{x}}{m}}\right)}
where
M
y
{\displaystyle M_{y}}
M
x
{\displaystyle M_{x}}
M
y
=
lim
m
,
n
→
∞
∑
i
=
1
m
∑
j
=
1
n
x
i
j
∗
ρ
(
x
i
j
∗
,
y
i
j
∗
)
Δ
D
=
∬
D
x
ρ
(
x
,
y
)
d
x
d
y
{\displaystyle M_{y}=\lim _{m,n\to \infty }\,\sum _{i=1}^{m}\,\sum _{j=1}^{n}\,x{_{ij}}^{*}\,\rho \ (x{_{ij}}^{*},y{_{ij}}^{*})\,\Delta D=\iint _{D}x\,\rho \ (x,y)\,dx\,dy}
M
x
=
lim
m
,
n
→
∞
∑
i
=
1
m
∑
j
=
1
n
y
i
j
∗
ρ
(
x
i
j
∗
,
y
i
j
∗
)
Δ
D
=
∬
D
y
ρ
(
x
,
y
)
d
x
d
y
{\displaystyle M_{x}=\lim _{m,n\to \infty }\,\sum _{i=1}^{m}\,\sum _{j=1}^{n}\,y{_{ij}}^{*}\,\rho \ (x{_{ij}}^{*},y{_{ij}}^{*})\,\Delta D=\iint _{D}y\,\rho \ (x,y)\,dx\,dy}
with summation and integration taken over a planar domain
D
{\displaystyle D}
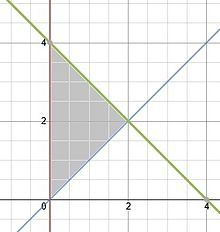
Example [ edit ] Find the center of mass of a lamina with edges given by the lines
x
=
0
,
{\displaystyle x=0,}
y
=
x
{\displaystyle y=x}
y
=
4
−
x
{\displaystyle y=4-x}
ρ
(
x
,
y
)
=
2
x
+
3
y
+
2
{\displaystyle \rho \ (x,y)\,=2x+3y+2}
For this the mass
m
{\displaystyle m}
M
y
{\displaystyle M_{y}}
M
x
{\displaystyle M_{x}}
Mass is
m
=
∬
D
ρ
(
x
,
y
)
d
x
d
y
{\displaystyle m=\iint _{D}\rho (x,y)\,dx\,dy}
iterated integral :
m
=
∫
x
=
0
2
∫
y
=
x
4
−
x
(
2
x
+
3
y
+
2
)
d
y
d
x
{\displaystyle m=\int _{x=0}^{2}\int _{y=x}^{4-x}\,(2x+3y+2)\,dy\,dx}
The inner integral is:
∫
y
=
x
4
−
x
(
2
x
+
3
y
+
2
)
d
y
{\displaystyle \int _{y=x}^{4-x}\,(2x+3y+2)\,dy}
=
(
2
x
y
+
3
y
2
2
+
2
y
)
|
y
=
x
4
−
x
{\displaystyle \qquad =\left.\left(2xy+{\frac {3y^{2}}{2}}+2y\right)\right|_{y=x}^{4-x}}
=
[
2
x
(
4
−
x
)
+
3
(
4
−
x
)
2
2
+
2
(
4
−
x
)
]
−
[
2
x
(
x
)
+
3
(
x
)
2
2
+
2
(
x
)
]
{\displaystyle \qquad =\left[2x(4-x)+{\frac {3(4-x)^{2}}{2}}+2(4-x)\right]-\left[2x(x)+{\frac {3(x)^{2}}{2}}+2(x)\right]}
=
−
4
x
2
−
8
x
+
32
{\displaystyle \qquad =-4x^{2}-8x+32}
Plugging this into the outer integral results in:
m
=
∫
x
=
0
2
(
−
4
x
2
−
8
x
+
32
)
d
x
=
(
−
4
x
3
3
−
4
x
2
+
32
x
)
|
x
=
0
2
=
112
3
{\displaystyle {\begin{aligned}m&=\int _{x=0}^{2}\left(-4x^{2}-8x+32\right)\,dx\\&=\left.\left(-{\frac {4x^{3}}{3}}-4x^{2}+32x\right)\right|_{x=0}^{2}\\&={\frac {112}{3}}\end{aligned}}}
Similarly are calculated both moments:
M
y
=
∬
D
x
ρ
(
x
,
y
)
d
x
d
y
=
∫
x
=
0
2
∫
y
=
x
4
−
x
x
(
2
x
+
3
y
+
2
)
d
y
d
x
{\displaystyle M_{y}=\iint _{D}x\,\rho (x,y)\,dx\,dy=\int _{x=0}^{2}\int _{y=x}^{4-x}x\,(2x+3y+2)\,dy\,dx}
with the inner integral:
∫
y
=
x
4
−
x
x
(
2
x
+
3
y
+
2
)
d
y
{\displaystyle \int _{y=x}^{4-x}x\,(2x+3y+2)\,dy}
=
(
2
x
2
y
+
3
x
y
2
2
+
2
x
y
)
|
y
=
x
4
−
x
{\displaystyle \qquad =\left.\left(2x^{2}y+{\frac {3xy^{2}}{2}}+2xy\right)\right|_{y=x}^{4-x}}
=
−
4
x
3
−
8
x
2
+
32
x
{\displaystyle \qquad =-4x^{3}-8x^{2}+32x}
which makes:
M
y
=
∫
x
=
0
2
(
−
4
x
3
−
8
x
2
+
32
x
)
d
x
=
(
−
x
4
−
8
x
3
3
+
16
x
2
)
|
x
=
0
2
=
80
3
{\displaystyle {\begin{aligned}M_{y}&=\int _{x=0}^{2}(-4x^{3}-8x^{2}+32x)\,dx\\&=\left.\left(-x^{4}-{\frac {8x^{3}}{3}}+16x^{2}\right)\right|_{x=0}^{2}\\&={\frac {80}{3}}\end{aligned}}}
and
M
x
=
∬
D
y
ρ
(
x
,
y
)
d
x
d
y
=
∫
x
=
0
2
∫
y
=
x
4
−
x
y
(
2
x
+
3
y
+
2
)
d
y
d
x
=
∫
0
2
(
x
y
2
+
y
3
+
y
2
)
|
y
=
x
4
−
x
d
x
=
∫
0
2
(
−
2
x
3
+
4
x
2
−
40
x
+
80
)
d
x
=
(
−
x
4
2
+
4
x
3
3
−
20
x
2
+
80
x
)
|
x
=
0
2
=
248
3
{\displaystyle {\begin{aligned}M_{x}&=\iint _{D}y\,\rho (x,y)\,dx\,dy=\int _{x=0}^{2}\int _{y=x}^{4-x}y\,(2x+3y+2)\,dy\,dx\\&=\int _{0}^{2}(xy^{2}+y^{3}+y^{2}){\Big |}_{y=x}^{4-x}\,dx\\&=\int _{0}^{2}(-2x^{3}+4x^{2}-40x+80)\,dx\\&=\left.\left(-{\frac {x^{4}}{2}}+{\frac {4x^{3}}{3}}-20x^{2}+80x\right)\right|_{x=0}^{2}\\&={\frac {248}{3}}\end{aligned}}}
Finally, the center of mass is
(
M
y
m
,
M
x
m
)
=
(
80
3
112
3
,
248
3
112
3
)
=
(
5
7
,
31
14
)
{\displaystyle \left({\frac {M_{y}}{m}},{\frac {M_{x}}{m}}\right)=\left({\frac {\frac {80}{3}}{\frac {112}{3}}},{\frac {\frac {248}{3}}{\frac {112}{3}}}\right)=\left({\frac {5}{7}},{\frac {31}{14}}\right)}
References [ edit ]
^ Atkins, Tony; Escudier, Marcel (2013), "Plane lamina" , A Dictionary of Mechanical Engineering (1 ed.) , Oxford University Press , doi :10.1093/acref/9780199587438.001.0001 , ISBN 9780199587438 , retrieved 2021-06-08 ^ "Planar Laminae" , WolframAlpha , retrieved 2021-03-09 ^ "Lamina" . MathWorld . Retrieved 2021-03-09 .

















![{\displaystyle \qquad =\left[2x(4-x)+{\frac {3(4-x)^{2}}{2}}+2(4-x)\right]-\left[2x(x)+{\frac {3(x)^{2}}{2}}+2(x)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2bc174897e803d0dc005ec5aaf9ba3363d2f958d)








