Quadrifolium
Appearance


The quadrifolium (also known as four-leaved clover[1]) is a type of rose curve with an angular frequency of 2. It has the polar equation:
with corresponding algebraic equation
Rotated counter-clockwise by 45°, this becomes
with corresponding algebraic equation
In either form, it is a plane algebraic curve of genus zero.
The dual curve to the quadrifolium is
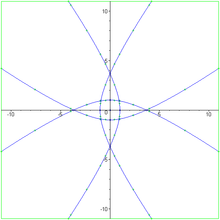
The area inside the quadrifolium is , which is exactly half of the area of the circumcircle of the quadrifolium. The perimeter of the quadrifolium is
where is the complete elliptic integral of the second kind with modulus , is the arithmetic–geometric mean and denotes the derivative with respect to the second variable.[2]
Notes
[edit]- ^ C G Gibson, Elementary Geometry of Algebraic Curves, An Undergraduate Introduction, Cambridge University Press, Cambridge, 2001, ISBN 978-0-521-64641-3. Pages 92 and 93
- ^ Quadrifolium - from Wolfram MathWorld
References
[edit]- J. Dennis Lawrence (1972). A catalog of special plane curves. Dover Publications. p. 175. ISBN 0-486-60288-5.











