Quadrupole magnet
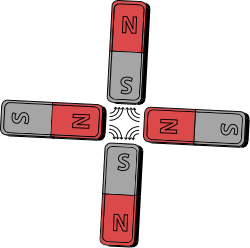
Quadrupole magnets, abbreviated as Q-magnets, consist of groups of four magnets laid out so that in the planar multipole expansion of the field, the dipole terms cancel and where the lowest significant terms in the field equations are quadrupole. Quadrupole magnets are useful as they create a magnetic field whose magnitude grows rapidly with the radial distance from its longitudinal axis. This is used in particle beam focusing.
The simplest magnetic quadrupole is two identical bar magnets parallel to each other such that the north pole of one is next to the south of the other and vice versa. Such a configuration will have no dipole moment, and its field will decrease at large distances faster than that of a dipole. A stronger version with very little external field involves using a k=3 Halbach cylinder.
In some designs of quadrupoles using electromagnets, there are four steel pole tips: two opposing magnetic north poles and two opposing magnetic south poles. The steel is magnetized by a large electric current in the coils of tubing wrapped around the poles. Another design is a Helmholtz coil layout but with the current in one of the coils reversed.[1]
Quadrupoles in particle accelerators[edit]


At the particle speeds reached in high energy particle accelerators, the magnetic force term is larger than the electric term in the Lorentz force:
and thus magnetic deflection is more effective than electrostatic deflection. Therefore a 'lattice' of electromagnets is used to bend, steer and focus a charged particle beam.

The quadrupoles in the lattice are of two types: 'F quadrupoles' (which are horizontally focusing but vertically defocusing) and 'D quadrupoles' (which are vertically focusing but horizontally defocusing). This situation is due to the laws of electromagnetism (the Maxwell equations) which show that it is impossible for a quadrupole to focus in both planes at the same time. The image on the right shows an example of a quadrupole focusing in the vertical direction for a positively charged particle going into the image plane (forces above and below the center point towards the center) while defocusing in the horizontal direction (forces left and right of the center point away from the center).
If an F quadrupole and a D quadrupole are placed immediately next to each other, their fields completely cancel out (in accordance with Earnshaw's theorem). But if there is a space between them (and the length of this has been correctly chosen), the overall effect is focusing in both horizontal and vertical planes. A lattice can then be built up enabling the transport of the beam over long distances—for example round an entire ring. A common lattice is a FODO lattice consisting of a basis of a focusing quadrupole, 'nothing' (often a bending magnet), a defocusing quadrupole and another length of 'nothing'.
Equations of motion and focal length for charged particles[edit]
A charged particle beam in a quadrupole magnetic field will experience a focusing / defocusing force in the transverse direction. This focusing effect is summed up by a focusing strength which depends on the quadrupole gradient as well as the beam's rigidity , where is the electric charge of the particle and
is the relativistic momentum. The focusing strength is given by
- ,
and particles in the magnetic will behave according to the ODE[2]
- .
The same equation will be true for the y direction, but with a minus sign in front of the focusing strength to account for the field changing directions.
Quadrupole ideal field[edit]
The components of the ideal magnetic field in the plane transverse to the beam are given by the following[3] (see also multipole magnet).
where is the field gradient of the normal quadrupole component and is the field gradient of the skew quadrupole component. The SI unit of the field gradients are . The field in a normal quadrupole is such that the magnetic poles are arranged with an angle of 45 degrees to the horizontal and vertical planes. The sign of determines whether (for a fixed particle charge and direction) the quadrupole focuses or defocuses particles in the horizontal plane.
See also[edit]
- Charged particle beam
- Dipole magnet
- Electron optics
- Halbach cylinder
- Sextupole magnet
- Multipole magnet
- Accelerator physics
References[edit]
- ^ Quadrupole Magnetic Field
- ^ Steven M. Lund, Transverse Particle Dynamics, US Particle Accelerator School (USPAS) Lectures on “Beam Physics with Intense SpaceCharge” https://people.nscl.msu.edu/~lund/uspas/bpisc_2017/lec_set_02/tpd.pdf
- ^ Shepard, Ben. "Conventional Magnets for Accelerators" (PDF).
External links[edit]
 Media related to Quadrupole magnet at Wikimedia Commons
Media related to Quadrupole magnet at Wikimedia Commons




![{\displaystyle [B\rho ]=p/q}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d03a61c7a9087342f07acfa278294ddd1a9b1d02)


![{\displaystyle \kappa ={\frac {G}{[B\rho ]}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/008271e0dcb6b947bec953a9e60043c747f2fe55)




