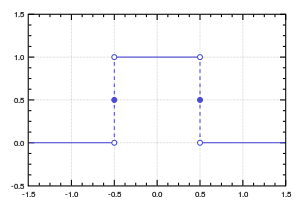
Function whose graph is 0, then 1, then 0 again, in an almost-everywhere continuous way
Rectangular function with a = 1 The rectangular function (also known as the rectangle function , rect function , Pi function , Heaviside Pi function ,[1] gate function , unit pulse , or the normalized boxcar function ) is defined as[2]
rect
(
t
a
)
=
Π
(
t
a
)
=
{
0
,
if
|
t
|
>
a
2
1
2
,
if
|
t
|
=
a
2
1
,
if
|
t
|
<
a
2
.
{\displaystyle \operatorname {rect} \left({\frac {t}{a}}\right)=\Pi \left({\frac {t}{a}}\right)=\left\{{\begin{array}{rl}0,&{\text{if }}|t|>{\frac {a}{2}}\\{\frac {1}{2}},&{\text{if }}|t|={\frac {a}{2}}\\1,&{\text{if }}|t|<{\frac {a}{2}}.\end{array}}\right.}
Alternative definitions of the function define
rect
(
±
1
2
)
{\textstyle \operatorname {rect} \left(\pm {\frac {1}{2}}\right)}
[3] [4] [5]
Its periodic version is called a rectangular wave
History [ edit ] The rect function has been introduced by Woodward [6] [7] cutout operator , together with the sinc function[8] [9] interpolation operator , and their counter operations which are sampling (comb operatorreplicating (rep operator
Relation to the boxcar function [ edit ] The rectangular function is a special case of the more general boxcar function :
rect
(
t
−
X
Y
)
=
H
(
t
−
(
X
−
Y
/
2
)
)
−
H
(
t
−
(
X
+
Y
/
2
)
)
=
H
(
t
−
X
+
Y
/
2
)
−
H
(
t
−
X
−
Y
/
2
)
{\displaystyle \operatorname {rect} \left({\frac {t-X}{Y}}\right)=H(t-(X-Y/2))-H(t-(X+Y/2))=H(t-X+Y/2)-H(t-X-Y/2)}
where
H
(
x
)
{\displaystyle H(x)}
Heaviside step function ; the function is centered at
X
{\displaystyle X}
Y
{\displaystyle Y}
X
−
Y
/
2
{\displaystyle X-Y/2}
X
+
Y
/
2.
{\displaystyle X+Y/2.}
Fourier transform of the rectangular function [ edit ] Plot of normalized
sinc
(
x
)
{\displaystyle \operatorname {sinc} (x)}
sinc
(
π
x
)
{\displaystyle \operatorname {sinc} (\pi x)}
The unitary Fourier transforms of the rectangular function are[2]
∫
−
∞
∞
rect
(
t
)
⋅
e
−
i
2
π
f
t
d
t
=
sin
(
π
f
)
π
f
=
sinc
π
(
f
)
,
{\displaystyle \int _{-\infty }^{\infty }\operatorname {rect} (t)\cdot e^{-i2\pi ft}\,dt={\frac {\sin(\pi f)}{\pi f}}=\operatorname {sinc} _{\pi }(f),}
using ordinary frequency
f , where
sinc
π
{\displaystyle \operatorname {sinc} _{\pi }}
is the normalized form
[10] of the
sinc function and
1
2
π
∫
−
∞
∞
rect
(
t
)
⋅
e
−
i
ω
t
d
t
=
1
2
π
⋅
sin
(
ω
/
2
)
ω
/
2
=
1
2
π
sinc
(
ω
/
2
)
,
{\displaystyle {\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\infty }\operatorname {rect} (t)\cdot e^{-i\omega t}\,dt={\frac {1}{\sqrt {2\pi }}}\cdot {\frac {\sin \left(\omega /2\right)}{\omega /2}}={\frac {1}{\sqrt {2\pi }}}\operatorname {sinc} \left(\omega /2\right),}
using angular frequency
ω
{\displaystyle \omega }
, where
sinc
{\displaystyle \operatorname {sinc} }
is the unnormalized form of the
sinc function .
For
rect
(
x
/
a
)
{\displaystyle \operatorname {rect} (x/a)}
∫
−
∞
∞
rect
(
t
a
)
⋅
e
−
i
2
π
f
t
d
t
=
a
sin
(
π
a
f
)
π
a
f
=
a
sinc
π
(
a
f
)
.
{\displaystyle \int _{-\infty }^{\infty }\operatorname {rect} \left({\frac {t}{a}}\right)\cdot e^{-i2\pi ft}\,dt=a{\frac {\sin(\pi af)}{\pi af}}=a\ \operatorname {sinc} _{\pi }{(af)}.}
Note that as long as the definition of the pulse function is only motivated by its behavior in the time-domain experience, there is no reason to believe that the oscillatory interpretation (i.e. the Fourier transform function) should be intuitive, or directly understood by humans. However, some aspects of the theoretical result may be understood intuitively, as finiteness in time domain corresponds to an infinite frequency response. (Vice versa, a finite Fourier transform will correspond to infinite time domain response.)
Relation to the triangular function [ edit ] We can define the triangular function as the convolution of two rectangular functions:
tri
=
rect
∗
rect
.
{\displaystyle \operatorname {tri} =\operatorname {rect} *\operatorname {rect} .\,}
Use in probability [ edit ] Viewing the rectangular function as a probability density function , it is a special case of the continuous uniform distribution with
a
=
−
1
/
2
,
b
=
1
/
2.
{\displaystyle a=-1/2,b=1/2.}
characteristic function is
φ
(
k
)
=
sin
(
k
/
2
)
k
/
2
,
{\displaystyle \varphi (k)={\frac {\sin(k/2)}{k/2}},}
and its moment-generating function is
M
(
k
)
=
sinh
(
k
/
2
)
k
/
2
,
{\displaystyle M(k)={\frac {\sinh(k/2)}{k/2}},}
where
sinh
(
t
)
{\displaystyle \sinh(t)}
hyperbolic sine function.
Rational approximation [ edit ] The pulse function may also be expressed as a limit of a rational function :
Π
(
t
)
=
lim
n
→
∞
,
n
∈
(
Z
)
1
(
2
t
)
2
n
+
1
.
{\displaystyle \Pi (t)=\lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}.}
Demonstration of validity [ edit ] First, we consider the case where
|
t
|
<
1
2
.
{\textstyle |t|<{\frac {1}{2}}.}
(
2
t
)
2
n
{\textstyle (2t)^{2n}}
n
.
{\displaystyle n.}
2
t
<
1
{\displaystyle 2t<1}
(
2
t
)
2
n
{\textstyle (2t)^{2n}}
n
.
{\displaystyle n.}
It follows that:
lim
n
→
∞
,
n
∈
(
Z
)
1
(
2
t
)
2
n
+
1
=
1
0
+
1
=
1
,
|
t
|
<
1
2
.
{\displaystyle \lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}={\frac {1}{0+1}}=1,|t|<{\tfrac {1}{2}}.}
Second, we consider the case where
|
t
|
>
1
2
.
{\textstyle |t|>{\frac {1}{2}}.}
(
2
t
)
2
n
{\textstyle (2t)^{2n}}
n
.
{\displaystyle n.}
2
t
>
1
{\displaystyle 2t>1}
(
2
t
)
2
n
{\textstyle (2t)^{2n}}
n
.
{\displaystyle n.}
It follows that:
lim
n
→
∞
,
n
∈
(
Z
)
1
(
2
t
)
2
n
+
1
=
1
+
∞
+
1
=
0
,
|
t
|
>
1
2
.
{\displaystyle \lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}={\frac {1}{+\infty +1}}=0,|t|>{\tfrac {1}{2}}.}
Third, we consider the case where
|
t
|
=
1
2
.
{\textstyle |t|={\frac {1}{2}}.}
lim
n
→
∞
,
n
∈
(
Z
)
1
(
2
t
)
2
n
+
1
=
lim
n
→
∞
,
n
∈
(
Z
)
1
1
2
n
+
1
=
1
1
+
1
=
1
2
.
{\displaystyle \lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}=\lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{1^{2n}+1}}={\frac {1}{1+1}}={\tfrac {1}{2}}.}
We see that it satisfies the definition of the pulse function. Therefore,
rect
(
t
)
=
Π
(
t
)
=
lim
n
→
∞
,
n
∈
(
Z
)
1
(
2
t
)
2
n
+
1
=
{
0
if
|
t
|
>
1
2
1
2
if
|
t
|
=
1
2
1
if
|
t
|
<
1
2
.
{\displaystyle \operatorname {rect} (t)=\Pi (t)=\lim _{n\rightarrow \infty ,n\in \mathbb {(} Z)}{\frac {1}{(2t)^{2n}+1}}={\begin{cases}0&{\mbox{if }}|t|>{\frac {1}{2}}\\{\frac {1}{2}}&{\mbox{if }}|t|={\frac {1}{2}}\\1&{\mbox{if }}|t|<{\frac {1}{2}}.\\\end{cases}}}
Dirac delta function [ edit ] The rectangle function can be used to represent the Dirac delta function
δ
(
x
)
{\displaystyle \delta (x)}
[11]
δ
(
x
)
=
lim
a
→
0
1
a
rect
(
x
a
)
.
{\displaystyle \delta (x)=\lim _{a\to 0}{\frac {1}{a}}\operatorname {rect} \left({\frac {x}{a}}\right).}
For a function
g
(
x
)
{\displaystyle g(x)}
, its average over the width
a
{\displaystyle a}
around 0 in the function domain is calculated as,
g
a
v
g
(
0
)
=
1
a
∫
−
∞
∞
d
x
g
(
x
)
rect
(
x
a
)
.
{\displaystyle g_{avg}(0)={\frac {1}{a}}\int \limits _{-\infty }^{\infty }dx\ g(x)\operatorname {rect} \left({\frac {x}{a}}\right).}
To obtain
g
(
0
)
{\displaystyle g(0)}
, the following limit is applied,
g
(
0
)
=
lim
a
→
0
1
a
∫
−
∞
∞
d
x
g
(
x
)
rect
(
x
a
)
{\displaystyle g(0)=\lim _{a\to 0}{\frac {1}{a}}\int \limits _{-\infty }^{\infty }dx\ g(x)\operatorname {rect} \left({\frac {x}{a}}\right)}
and this can be written in terms of the Dirac delta function as,
g
(
0
)
=
∫
−
∞
∞
d
x
g
(
x
)
δ
(
x
)
.
{\displaystyle g(0)=\int \limits _{-\infty }^{\infty }dx\ g(x)\delta (x).}
The Fourier transform of the Dirac delta function
δ
(
t
)
{\displaystyle \delta (t)}
is
δ
(
f
)
=
∫
−
∞
∞
δ
(
t
)
⋅
e
−
i
2
π
f
t
d
t
=
lim
a
→
0
1
a
∫
−
∞
∞
rect
(
t
a
)
⋅
e
−
i
2
π
f
t
d
t
=
lim
a
→
0
sinc
(
a
f
)
.
{\displaystyle \delta (f)=\int _{-\infty }^{\infty }\delta (t)\cdot e^{-i2\pi ft}\,dt=\lim _{a\to 0}{\frac {1}{a}}\int _{-\infty }^{\infty }\operatorname {rect} \left({\frac {t}{a}}\right)\cdot e^{-i2\pi ft}\,dt=\lim _{a\to 0}\operatorname {sinc} {(af)}.}
where the
sinc function here is the normalized sinc function. Because the first zero of the sinc function is at
f
=
1
/
a
{\displaystyle f=1/a}
and
a
{\displaystyle a}
goes to infinity, the Fourier transform of
δ
(
t
)
{\displaystyle \delta (t)}
is
δ
(
f
)
=
1
,
{\displaystyle \delta (f)=1,}
means that the frequency spectrum of the Dirac delta function is infinitely broad. As a pulse is shorten in time, it is larger in spectrum.
See also [ edit ] References [ edit ]
^ Wolfram Research (2008). "HeavisidePi, Wolfram Language function" . Retrieved October 11, 2022 . ^ a b Weisstein, Eric W. "Rectangle Function" . MathWorld ^ Wang, Ruye (2012). Introduction to Orthogonal Transforms: With Applications in Data Processing and Analysis ISBN 9780521516884 ^ Tang, K. T. (2007). Mathematical Methods for Engineers and Scientists: Fourier analysis, partial differential equations and variational models ISBN 9783540446958 ^ Kumar, A. Anand (2011). Signals and Systems ISBN 9788120343108 ^ Klauder, John R (1960). "The Theory and Design of Chirp Radars" . Bell System Technical Journal . 39 (4): 745–808. doi :10.1002/j.1538-7305.1960.tb03942.x . ^ Woodward, Philipp M (1953). Probability and Information Theory, with Applications to Radar . Pergamon Press. p. 29. ^ Higgins, John Rowland (1996). Sampling Theory in Fourier and Signal Analysis: Foundations . Oxford University Press Inc. p. 4. ISBN 0198596995 ^ Zayed, Ahmed I (1996). Handbook of Function and Generalized Function Transformations . CRC Press. p. 507. ISBN 9780849380761 ^ Wolfram MathWorld, https://mathworld.wolfram.com/SincFunction.html
^ Khare, Kedar; Butola, Mansi; Rajora, Sunaina (2023). "Chapter 2.4 Sampling by Averaging, Distributions and Delta Function". Fourier Optics and Computational Imaging (2nd ed.). Springer. pp. 15–16. doi :10.1007/978-3-031-18353-9 . ISBN 978-3-031-18353-9