Image scaling

In computer graphics and digital imaging, image scaling refers to the resizing of a digital image. In video technology, the magnification of digital material is known as upscaling or resolution enhancement.
When scaling a vector graphic image, the graphic primitives that make up the image can be scaled using geometric transformations with no loss of image quality. When scaling a raster graphics image, a new image with a higher or lower number of pixels must be generated. In the case of decreasing the pixel number (scaling down), this usually results in a visible quality loss. From the standpoint of digital signal processing, the scaling of raster graphics is a two-dimensional example of sample-rate conversion, the conversion of a discrete signal from a sampling rate (in this case, the local sampling rate) to another.
Mathematical[edit]
Image scaling can be interpreted as a form of image resampling or image reconstruction from the view of the Nyquist sampling theorem. According to the theorem, downsampling to a smaller image from a higher-resolution original can only be carried out after applying a suitable 2D anti-aliasing filter to prevent aliasing artifacts. The image is reduced to the information that can be carried by the smaller image.
In the case of up sampling, a reconstruction filter takes the place of the anti-aliasing filter.
-
Original 160x160px image
-
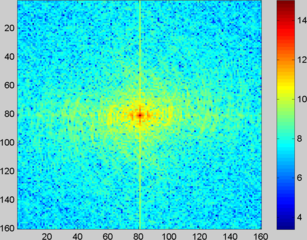
Original image in spatial-frequency domain
-
2D low-pass filtered, but still at 160x160px
-
Filtered image in spatial-frequency domain
-
low-pass filtered 160x160px image 4× downsampled to 40x40px
-
4× Fourier upsampling of 40x40px downsampled image to 160x160px (correct reconstruction)
-
4× Fourier upsampling of 40x40px downsampled image to 160x160px (with aliasing)
A more sophisticated approach to upscaling treats the problem as an inverse problem, solving the question of generating a plausible image that, when scaled down, would look like the input image. A variety of techniques have been applied for this, including optimization techniques with regularization terms and the use of machine learning from examples.
Algorithms[edit]
An image size can be changed in several ways.
Nearest-neighbor interpolation[edit]
One of the simpler ways of increasing image size is nearest-neighbor interpolation, replacing every pixel with the nearest pixel in the output; for upscaling, this means multiple pixels of the same color will be present. This can preserve sharp details in pixel art but also introduce jaggedness in previously smooth images. 'Nearest' in nearest-neighbor does not have to be the mathematical nearest. One common implementation is to always round toward zero. Rounding this way produces fewer artifacts and is faster to calculate.[citation needed]
Bilinear and bicubic algorithms[edit]
Bilinear interpolation works by interpolating pixel color values, introducing a continuous transition into the output even where the original material has discrete transitions. Although this is desirable for continuous-tone images, this algorithm reduces contrast (sharp edges) in a way that may be undesirable for line art. Bicubic interpolation yields substantially better results, with an increase in computational cost.[citation needed]
Sinc and Lanczos resampling[edit]
Sinc resampling, in theory, provides the best possible reconstruction for a perfectly bandlimited signal. In practice, the assumptions behind sinc resampling are not completely met by real-world digital images. Lanczos resampling, an approximation to the sinc method, yields better results. Bicubic interpolation can be regarded as a computationally efficient approximation to Lanczos resampling.[citation needed]
Box sampling[edit]
One weakness of bilinear, bicubic, and related algorithms is that they sample a specific number of pixels. When downscaling below a certain threshold, such as more than twice for all bi-sampling algorithms, the algorithms will sample non-adjacent pixels, which results in both losing data and rough results.[citation needed]
The trivial solution to this issue is box sampling, which is to consider the target pixel a box on the original image and sample all pixels inside the box. This ensures that all input pixels contribute to the output. The major weakness of this algorithm is that it is hard to optimize.[citation needed]
Mipmap[edit]
Another solution to the downscale problem of bi-sampling scaling is mipmaps. A mipmap is a prescaled set of downscaled copies. When downscaling, the nearest larger mipmap is used as the origin to ensure no scaling below the useful threshold of bilinear scaling. This algorithm is fast and easy to optimize. It is standard in many frameworks, such as OpenGL. The cost is using more image memory, exactly one-third more in the standard implementation.
Fourier-transform methods[edit]
Simple interpolation based on the Fourier transform pads the frequency domain with zero components (a smooth window-based approach would reduce the ringing). Besides the good conservation (or recovery) of details, notable are the ringing and the circular bleeding of content from the left border to the right border (and the other way around).
Edge-directed interpolation[edit]
Edge-directed interpolation algorithms aim to preserve edges in the image after scaling, unlike other algorithms, which can introduce staircase artifacts.
Examples of algorithms for this task include New Edge-Directed Interpolation (NEDI),[1][2] Edge-Guided Image Interpolation (EGGI),[3] Iterative Curvature-Based Interpolation (ICBI),[citation needed] and Directional Cubic Convolution Interpolation (DCCI).[4] A 2013 analysis found that DCCI had the best scores in PSNR and SSIM on a series of test images.[5]
hqx[edit]
For magnifying computer graphics with low resolution and/or few colors (usually from 2 to 256 colors), better results can be achieved by hqx or other pixel-art scaling algorithms. These produce sharp edges and maintain a high level of detail.
Vectorization[edit]
Vector extraction, or vectorization, offers another approach. Vectorization first creates a resolution-independent vector representation of the graphic to be scaled. Then the resolution-independent version is rendered as a raster image at the desired resolution. This technique is used by Adobe Illustrator, Live Trace, and Inkscape.[6] Scalable Vector Graphics are well suited to simple geometric images, while photographs do not fare well with vectorization due to their complexity.
Deep convolutional neural networks[edit]
This method uses machine learning for more detailed images, such as photographs and complex artwork. Programs that use this method include waifu2x, Imglarger and Neural Enhance.
- Demonstration of conventional upscaling vs Waifu2x upscaling with noise reduction, using a detail of Phosphorus and Hesperus by Evelyn De Morgan. Click for full sizes.
-
Original image
-
Image upscaled 200% using PaintShop Pro
-
Image upscaled 200% using waifu2x in Photo mode with Medium noise reduction
-
Image upscaled 400% using Topaz A.I. Gigapixel with Low noise reduction
-
Image upscaled 400% using RealSR DF2K-JPEG
AI-driven software such as the MyHeritage Photo Enhancer allows detail and sharpness to be added to historical photographs, where it is not present in the original.
-
Low-quality 270×368 pixel photograph of John Howard Lindauer, scanned from a State Legislature directory
-
The same image enhanced and upscaled to 2160×2944 pixels by MyHeritage's Photo Enhancer
Applications[edit]
General[edit]
Image scaling is used in, among other applications, web browsers,[7] image editors, image and file viewers, software magnifiers, digital zoom, the process of generating thumbnail images, and when outputting images through screens or printers.
Video[edit]
This application is the magnification of images for home theaters for HDTV-ready output devices from PAL-Resolution content, for example, from a DVD player. Upscaling is performed in real time, and the output signal is not saved.
Pixel-art scaling[edit]
As pixel-art graphics are usually low-resolution, they rely on careful placement of individual pixels, often with a limited palette of colors. This results in graphics that rely on stylized visual cues to define complex shapes with little resolution, down to individual pixels. This makes scaling pixel art a particularly difficult problem.
Specialized algorithms[8] were developed to handle pixel-art graphics, as the traditional scaling algorithms do not take perceptual cues into account.
Since a typical application is to improve the appearance of fourth-generation and earlier video games on arcade and console emulators, many are designed to run in real time for small input images at 60 frames per second.
On fast hardware, these algorithms are suitable for gaming and other real-time image processing. These algorithms provide sharp, crisp graphics, while minimizing blur. Scaling art algorithms have been implemented in a wide range of emulators such as HqMAME and DOSBox, as well as 2D game engines and game engine recreations such as ScummVM. They gained recognition with gamers, for whom these technologies encouraged a revival of 1980s and 1990s gaming experiences.[citation needed]
Such filters are currently used in commercial emulators on Xbox Live, Virtual Console, and PSN to allow classic low-resolution games to be more visually appealing on modern HD displays. Recently released games that incorporate these filters include Sonic's Ultimate Genesis Collection, Castlevania: The Dracula X Chronicles, Castlevania: Symphony of the Night, and Akumajō Dracula X Chi no Rondo.
Real-time scaling[edit]
A number of companies have developed techniques to upscale video frames in real-time, such as when they are drawn on screen in a video game. Nvidia's deep learning super sampling (DLSS) uses deep learning to upsample lower-resolution images to a higher resolution for display on higher-resolution computer monitors.[9] AMD's FidelityFX Super Resolution 1.0 (FSR) does not employ machine learning, instead using traditional hand-written algorithms to achieve spatial upscaling on traditional shading units. FSR 2.0 utilises temporal upscaling, again with a hand-tuned algorithm. FSR standardized presets are not enforced, and some titles such as Dota 2 offer resolution sliders.[10] Other technologies include Intel XeSS and Nvidia Image Scaler (NIS).[11][12]
See also[edit]
- Bicubic interpolation
- Bilinear interpolation
- Image reconstruction
- Lanczos resampling
- Spline interpolation
- Seam carving
- Video scaler
- Scaling (geometry)
References[edit]
- ^ "Edge-Directed Interpolation". Retrieved 19 February 2016.
- ^ Xin Li; Michael T. Orchard. "NEW EDGE DIRECTED INTERPOLATION" (PDF). 2000 IEEE International Conference on Image Processing: 311. Archived from the original (PDF) on 14 February 2016.
- ^ Zhang, D.; Xiaolin Wu (2006). "An Edge-Guided Image Interpolation Algorithm via Directional Filtering and Data Fusion". IEEE Transactions on Image Processing. 15 (8): 2226–38. Bibcode:2006ITIP...15.2226Z. doi:10.1109/TIP.2006.877407. PMID 16900678. S2CID 9760560.
- ^ Dengwen Zhou; Xiaoliu Shen. "Image Zooming Using Directional Cubic Convolution Interpolation". Retrieved 13 September 2015.
- ^ Shaode Yu; Rongmao Li; Rui Zhang; Mou An; Shibin Wu; Yaoqin Xie (2013). "Performance evaluation of edge-directed interpolation methods for noise-free images". arXiv:1303.6455 [cs.CV].
- ^ Johannes Kopf and Dani Lischinski (2011). "Depixelizing Pixel Art". ACM Transactions on Graphics. 30 (4): 99:1–99:8. doi:10.1145/2010324.1964994. Archived from the original on 1 September 2015. Retrieved 24 October 2012.
- ^ Analysis of image scaling algorithms used by popular web browsers
- ^ "Pixel Scalers". Retrieved 19 February 2016.
- ^ "NVIDIA DLSS: Your Questions, Answered". www.nvidia.com. Archived from the original on 5 October 2021. Retrieved 13 October 2021.
- ^ "Valve's Dota 2 Adds AMD FidelityFX Super Resolution - Phoronix". www.phoronix.com. Archived from the original on 21 July 2021. Retrieved 13 October 2021.
- ^ Gartenberg, Chaim (19 August 2021). "Intel shows off its answer to Nvidia's DLSS, coming to Arc GPUs in 2022". The Verge. Archived from the original on 19 August 2021. Retrieved 13 October 2021.
- ^ "What Is Nvidia Image Scaling? Upscaling Tech, Explained". Digital Trends. 16 November 2021. Retrieved 3 December 2021.