Zero of a function
In mathematics, a zero (also sometimes called a root) of a real-, complex-, or generally vector-valued function , is a member of the domain of such that vanishes at ; that is, the function attains the value of 0 at , or equivalently, is a solution to the equation .[1] A "zero" of a function is thus an input value that produces an output of 0.[2]
A root of a polynomial is a zero of the corresponding polynomial function.[1] The fundamental theorem of algebra shows that any non-zero polynomial has a number of roots at most equal to its degree, and that the number of roots and the degree are equal when one considers the complex roots (or more generally, the roots in an algebraically closed extension) counted with their multiplicities.[3] For example, the polynomial of degree two, defined by has the two roots (or zeros) that are 2 and 3.
If the function maps real numbers to real numbers, then its zeros are the -coordinates of the points where its graph meets the x-axis. An alternative name for such a point in this context is an -intercept.
Solution of an equation
[edit]Every equation in the unknown may be rewritten as
by regrouping all the terms in the left-hand side. It follows that the solutions of such an equation are exactly the zeros of the function . In other words, a "zero of a function" is precisely a "solution of the equation obtained by equating the function to 0", and the study of zeros of functions is exactly the same as the study of solutions of equations.
Polynomial roots
[edit]Every real polynomial of odd degree has an odd number of real roots (counting multiplicities); likewise, a real polynomial of even degree must have an even number of real roots. Consequently, real odd polynomials must have at least one real root (because the smallest odd whole number is 1), whereas even polynomials may have none. This principle can be proven by reference to the intermediate value theorem: since polynomial functions are continuous, the function value must cross zero, in the process of changing from negative to positive or vice versa (which always happens for odd functions).
Fundamental theorem of algebra
[edit]The fundamental theorem of algebra states that every polynomial of degree has complex roots, counted with their multiplicities. The non-real roots of polynomials with real coefficients come in conjugate pairs.[2] Vieta's formulas relate the coefficients of a polynomial to sums and products of its roots.
Computing roots
[edit]Computing roots of functions, for example polynomial functions, frequently requires the use of specialised or approximation techniques (e.g., Newton's method). However, some polynomial functions, including all those of degree no greater than 4, can have all their roots expressed algebraically in terms of their coefficients (for more, see algebraic solution).
Zero set
[edit]In various areas of mathematics, the zero set of a function is the set of all its zeros. More precisely, if is a real-valued function (or, more generally, a function taking values in some additive group), its zero set is , the inverse image of in .
Under the same hypothesis on the codomain of the function, a level set of a function is the zero set of the function for some in the codomain of
The zero set of a linear map is also known as its kernel.
The cozero set of the function is the complement of the zero set of (i.e., the subset of on which is nonzero).
Applications
[edit]In algebraic geometry, the first definition of an algebraic variety is through zero sets. Specifically, an affine algebraic set is the intersection of the zero sets of several polynomials, in a polynomial ring over a field. In this context, a zero set is sometimes called a zero locus.
In analysis and geometry, any closed subset of is the zero set of a smooth function defined on all of . This extends to any smooth manifold as a corollary of paracompactness.
In differential geometry, zero sets are frequently used to define manifolds. An important special case is the case that is a smooth function from to . If zero is a regular value of , then the zero set of is a smooth manifold of dimension by the regular value theorem.
For example, the unit -sphere in is the zero set of the real-valued function .
See also
[edit]- Marden's theorem
- Root-finding algorithm
- Sendov's conjecture
- Vanish at infinity
- Zero crossing
- Zeros and poles
References
[edit]- ^ a b "Algebra - Zeroes/Roots of Polynomials". tutorial.math.lamar.edu. Retrieved 2019-12-15.
- ^ a b Foerster, Paul A. (2006). Algebra and Trigonometry: Functions and Applications, Teacher's Edition (Classics ed.). Upper Saddle River, NJ: Prentice Hall. p. 535. ISBN 0-13-165711-9.
- ^ "Roots and zeros (Algebra 2, Polynomial functions)". Mathplanet. Retrieved 2019-12-15.

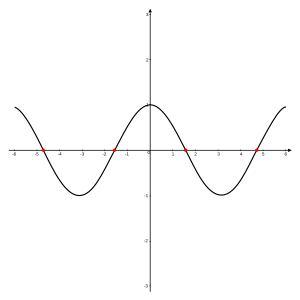


![{\displaystyle \left[-2\pi ,2\pi \right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cdc6c1efef56b12d350b9e16f34e39e317d5b51f)
















![{\displaystyle k\left[x_{1},\ldots ,x_{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/26e790118352b6852ad6a2e132d4c9819b896c45)





