Timed automaton
In automata theory, a timed automaton is a finite automaton extended with a finite set of real-valued clocks. During a run of a timed automaton, clock values increase all with the same speed. Along the transitions of the automaton, clock values can be compared to integers. These comparisons form guards that may enable or disable transitions and by doing so constrain the possible behaviors of the automaton. Further, clocks can be reset. Timed automata are a sub-class of a type hybrid automata.
Timed automata can be used to model and analyse the timing behavior of computer systems, e.g., real-time systems or networks. Methods for checking both safety and liveness properties have been developed and intensively studied over the last 20 years.
It has been shown that the state reachability problem for timed automata is decidable,[1] which makes this an interesting sub-class of hybrid automata. Extensions have been extensively studied, among them stopwatches, real-time tasks, cost functions, and timed games. There exists a variety of tools to input and analyse timed automata and extensions, including the model checkers UPPAAL, Kronos, and the schedulability analyser TIMES. These tools are becoming more and more mature, but are still all academic research tools.
Example[edit]
Before formally defining what a timed automaton is, some examples are given.
Consider the language of timed words over the unary alphabet such that there is an during the first time unit, and there is less than one time unit between two successive . A timed automaton recognizing this language, pictured nearby, uses a single clock , which should never be equal to one. This clock counts the time since the start of the run if no were emitted, or from the last emitted otherwise. This means that each time an is emitted, this clock is reset to zero.
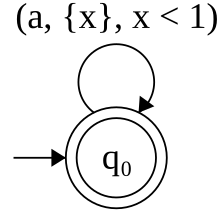
Consider the language of timed words over the binary alphabet such that each is followed by a in the next time unit. The timed automaton recognizing this language, pictured nearby, recalls whether or not there was an that was not yet followed by a . If it is not the case, it accepts the run, otherwise it rejects it. Furthermore, when there is such a , it has a clock that records the time elapsed since the first such was emitted. In this case, a cannot be emitted if the clock is at least equal to one, and thus the run fails.

Formal definition[edit]
Timed automaton[edit]
Formally, a timed automaton is a tuple that consists of the following components:
- is a finite set called the alphabet or actions of .
- is a finite set. The elements of are called the locations or states' of .
- is the set of start locations.
- is a finite set called the clocks of .
- is the set of accepting locations.
- is a set of edges, called transitions of , where
- is the set of clock constraints involving clocks from , and
- is the powerset of .
An edge from is a transition from locations to with action , guard and clock resets .
Extended state[edit]
A pair with a location and a clock valuation is called either an extended state or a state.
Note that the word state is thus ambiguous, since, depending on the author, it may mean either a pair or an element of . For the sake of the clarity, this article will use the term location for element of and the term extended location for pairs.
Here lies one of the biggest difference between timed automata and finite automata. In a finite automaton, at some point of the execution, the state is entirely described by the number of letter read and by a finite number of possible values, which are actually called "states". That means that, given a state and a suffix of the word to read, the remaining of the run is totally determined. Thus, the word "finite" in the name "finite automata". However, as it is explained in the section "run" below, in order to resume clocks are used to determine which transitions can be taken. Thus, in order to know the state of the automaton, you must both know in which location you are, and the clock valuation.
Run[edit]
Given a timed word with , an increasing sequence of non-negative number, and a timed automaton as above, a run is a sequence of the form satisfying the following constraint:
- (initialization)
- (consecution), for all , there exists an edge in of the form such that:
- we assume that time units passed, and at this time, the guard is satisfied. I.e. satisfies ,
- the new clock valuation corresponds to , in which time units passed and in which the clocks of where reset. Formally, .
The notion of accepting run is defined as in finite automata for finite words and as in Büchi automata for infinite words. That is, if is finite of length , then the run is accepting if . If the word is infinite, then the run is accepting if and only if there exists an infinite number of position such that .
Deterministic timed automaton[edit]
As in the case of finite and Büchi automaton, a timed automaton may be deterministic or non-deterministic. Intuitively, being deterministic has the same meaning in each of those case. It means that the set of start locations is a singleton, and that, given a state , and a letter , there is only one possible state which can be reached from by reading . However, in the case of timed automaton the formal definition is slightly more complex. Formally, a timed automaton is deterministic if:
- is a singleton
- for each pair of transitions and , the set of clocks valuations satisfying is disjoint from the set of clocks valuations satisfying .
Closure property[edit]
The class of languages recognized by non-deterministic timed automata is:
- closed under union, indeed, the disjoint union of two timed automata recognize the union of the language recognized by those automata.
- closed under intersection.[2]
- not closed under complement.[3]
Problems and their complexity[edit]
The computational complexity of some problems related to timed automata are now given.
The emptiness problem for timed automata can be solved by constructing a region automaton and checking whether it accepts the empty language. This problem is PSPACE-complete.[1]: 207
The universality problem of non-deterministic timed automaton is undecidable, and more precisely Π1
1. However, when the automaton contains a single clock, the property is decidable; however, it is not primitive recursive.[3] This problem consists of deciding whether every word is accepted by a timed automaton.
See also[edit]
- Alternating timed automaton: an extension of timed automaton with universal transitions.
Notes[edit]
- ^ a b Rajeev Alur, David L. Dill. 1994 A Theory of Timed Automata. In Theoretical Computer Science, vol. 126, 183–235, pp. 194–1955
- ^ Modern Applications Of Automata, page 118
- ^ a b Lasota, SƗawomir; Walukiewicz, Igor (2008). "Alternating Timed Automata". ACM Transactions on Computational Logic. 9 (2): 1–26. arXiv:cs/0512031. doi:10.1145/1342991.1342994. S2CID 12319.





























![{\displaystyle (\ell _{0},\nu _{0}){\xrightarrow[{t_{1}}]{\sigma _{1}}}(\ell _{1},\nu _{1})\dots }](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8c309e3b94c003f0154a3d726e110ec7a6040bc)









![{\displaystyle \nu _{i}=(\nu _{i-1}+t_{i}-t_{i-1})[r_{i}\rightarrow 0]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec515eb84e676601a93a2df9dc0dd3cec2f8f41d)







