User:Martin Hogbin/MHP - Proposal
Answer[edit]
The contestant should always switch to the other door; contestants who switch double their chances of winning the car by switching .
Simple explanations[edit]
Explanation 1[edit]
A simple and intuitive explanation is to reason that a player whose strategy is to switch loses if and only if the player initially picks the car, which happens with probability 1/3, so switching must win with probability 2/3 (Carlton 2005).
Explanation 2[edit]
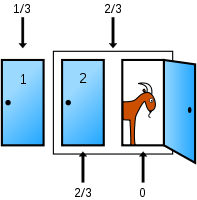
The analysis can be illustrated in terms of the equally likely events that the player has initially chosen the car, goat A, or goat B (Economist 1999):
| |||||||||||||||||||||||||||
The player has an equal chance of initially selecting the car, Goat A, or Goat B. Switching results in a win 2/3 of the time.
| |||||||||||||||||||||||||||
Explanation 3[edit]
The solution presented by vos Savant in Parade (vos Savant 1990b) shows the three possible arrangements of one car and two goats behind three doors and the result of staying or switching after initially picking door 1 in each case:
behind door 1 behind door 2 behind door 3 result if staying at door #1 result if switching to the door offered Car Goat Goat Car Goat Goat Car Goat Goat Car Goat Goat Car Goat Car
A player who stays with the initial choice wins in only one out of three of these equally likely possibilities, while a player who switches wins in two out of three. The probability of winning by staying with the initial choice is therefore 1/3, while the probability of winning by switching is 2/3.
Explanation 4[edit]
Another way to understand the solution is to consider the two original unchosen doors together. Instead of one door being opened and shown to be a losing door, an equivalent action is to combine the two unchosen doors into one since the player cannot choose the opened door (Adams 1990; Devlin 2003; Williams 2004; Stibel et al., 2008).
As Cecil Adams puts it (Adams 1990), "Monty is saying in effect: you can keep your one door or you can have the other two doors." The player therefore has the choice of either sticking with the original choice of door, or choosing the sum of the contents of the two other doors, as the 2/3 chance of hiding the car has not been changed by the opening of one of these doors.
As Keith Devlin says (Devlin 2003), "By opening his door, Monty is saying to the contestant 'There are two doors you did not choose, and the probability that the prize is behind one of them is 2/3. I'll help you by using my knowledge of where the prize is to open one of those two doors to show you that it does not hide the prize. You can now take advantage of this additional information. Your choice of door A has a chance of 1 in 3 of being the winner. I have not changed that. But by eliminating door C, I have shown you that the probability that door B hides the prize is 2 in 3.'"