User:Tom.vettenburg/sandbox

This is the user sandbox of Tom.vettenburg. A user sandbox is a subpage of the user's user page. It serves as a testing spot and page development space for the user and is not an encyclopedia article. Create or edit your own sandbox here.

Other sandboxes: Main sandbox | Template sandbox

Finished writing a draft article? Are you ready to request review of it by an experienced editor for possible inclusion in Wikipedia? Submit your draft for review!

The optical transfer function (OTF) is the transfer function of an optical system such as a camera, microscope, human eye, or projector. It is used by optical engineers and scientists to describe how the optics project light from the object or scene onto a photographic film, detector array, retina, or screen. The function specifies the translation and contrast reduction of a periodic sine pattern after passing through the lens system, as a function of its periodicity and orientation. Formally, the optical transfer function is defined as the Fourier transform of the point spread function, or impulse response of the optics, i.e. the image of a point source. When this image does not change shape up on lateral translation of the point source, the optical transfer function can be used to study the projection of arbitrary objects or scenes onto the detector or film. While figures of merit such as contrast, sensitivity, and resolution give an intuitive indication of performance, the optical transfer function provides a comprehensive and well-defined characterization of optical systems.

Definition and related concepts[edit]

Since the optical transfer function (OTF) is defined as the Fourier transform of the point-spread function (PSF), it is generally speaking a complex valued function. The projection of a specific periodic pattern is represented by a complex number with absolute value and complex argument proportional to the relative contrast and translation of the projected projection, respectively.

Often the contrast reduction is of most interest and the pattern translation can be ignored. The relative contrast is given by the absolute value of the optical transfer function, a function commonly referred to as the modulation transfer function (MTF). On the other hand, when also the pattern translation is important, the complex argument of the optical transfer function can be depicted as a second real-valued function, commonly referred to as the phase transfer function (PhTF). The complex-valued optical transfer function can be seen as a combination of these two real-valued functions:

\mathrm {OTF} (\nu )=\mathrm {MTF} (\nu )e^{i\,\mathrm {PhTF} (\nu )}

where

\mathrm {MTF} (\nu )=\left\vert \mathrm {OTF} (\nu )\right\vert

\mathrm {PhTF} (\nu )=\mathrm {arg} (\mathrm {OTF} (\nu )),

and $\mathrm {arg} (\cdot )$ represents the complex argument function, while $\nu$ is the spatial frequency of the periodic pattern. In general $\nu$ is a vector with a spatial frequency for each dimension, i.e. it indicates also the direction of the periodic pattern.

The impulse response of a well-focused optical system is a three-dimensional intensity distribution with a maximum at the focal plane, and could thus be measured by recording a stack of images while displacing the detector axially. By consequence, the three-dimensional optical transfer function can be defined as the three-dimensional Fourier transform of the impulse response. Although typically only a one-dimensional, or sometimes a two-dimensional section is used, the three-dimensional optical transfer function can improve the understanding of microscopes such as the structured illumination microscope.

True to the definition of transfer function, $\mathrm {OTF} (0)=\mathrm {MTF} (0)$ should indicate the fraction of light that was detected from the point source object. However, typically the contrast relative to the total amount of detected light is most important. It is thus common practice to normalize the optical transfer function to the detected intensity, hence $\mathrm {MTF} (\nu )\equiv 1$ .

Generally, the optical transfer function depends on factors such as the spectrum and polarization of the emitted light and the position of the point source. E.g. the image contrast and resolution are typically optimal At the center of the image, and deteriorate toward the edges of the field-of-view. When significant variation occurs, the optical transfer function may be calculated for a set of representative positions or colors.

Examples[edit]

The OTF of an ideal lens system[edit]

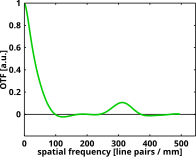
A perfect lens system will provide a high contrast projection without shifting the periodic pattern, hence the optical transfer function is identical to the modulation transfer function. Typically the contrast will reduce gradually towards zero at a point defined by the resolution of the optics. For example, a perfect, non-aberrated, f/4 optical imaging system used, at the visible wavelength of 500nm, would have the optical transfer function depicted in the right hand figure.

$One-dimensional optical transfer function of a diffraction limited imaging system is identical to its modulation transfer function.$

The one-dimensional optical transfer function of a diffraction limited imaging system is identical to its modulation transfer function.

$Spoke target imaged by a diffraction limited imaging system.$

Spoke target imaged by a diffraction limited imaging system.

Transfer function and example image of an ideal, optical-aberration-free (diffraction-limited) imaging system.

It can be read from the plot that the contrast gradually reduces and reaches zero at the spatial frequency of 500 cycles per millimeter, in other words the optical resolution of the image projection is 1/500^th of a millimeter, or 2 micrometer. Correspondingly, for this particular imaging device, the spokes become more and more blurred towards the center until they merge into a gray, unresolved, disc. Note that sometimes the optical transfer function is given in units of the object or sample space, observation angle, film width, or normalized to the theoretical maximum. Conversion between the two is typically a matter of a multiplication or division. E.g. a microscope typically magnifies everything 10 to 100-fold, and a reflex camera will generally demagnify objects at a distance of 5 meter by a factor of 100 to 200.

The resolution of a digital imaging device is not only limited by the optics, but also by the number of pixels, more in particular by their separation distance. As explained by the Nyquist-Shannon Theorem, to match the optical resolution of the given example, the pixels of each color channel should be separated by 1 micrometer, half the period of 500 cycles per millimeter. A higher number of pixels on the same sensor size will not allow the resolution of finer detail. On the other hand, when the pixel spacing is larger than 1 micrometer, the resolution will be limited by the separation between pixels; moreover, aliasing may lead to a further reduction of the image fidelity.

The OTF of an imperfect lens system[edit]

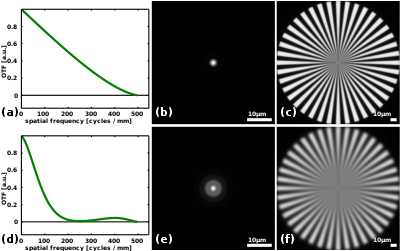
An imperfect, aberrated, imaging system could posses the the optical transfer function depicted in the following figure.

The real part of the optical transfer function of an aberrated, imperfect, imaging system.

The modulation transfer function of an aberrated, imperfect, imaging system.

The image of a spoke target as image by an aberrated optical system.

Transfer function and example image of an f/4 optical imaging system at 500nm with spherical aberration with standard Zernike coefficient of 0.25.

As the ideal lens system, the contrast reaches zero at the spatial frequency of 500 cycles per millimeter. However, at lower spatial frequencies the contrast is considerably lower than that of the perfect system in the previous example. In fact, the contrast becomes zero on several occasions even for spatial frequencies lower than 500 cycles per millimeter. This explains the gray circular bands in the spoke image shown in the above figure. In between the gray bands, the spokes appear to invert from black to white and visa versa, this is referred to as contrast inversion, directly related to the sign reversal in the real part of the optical transfer function, and represents itself as a shift by half a period for some periodic patterns.

While it could be argued that the resolution of both the ideal and the imperfect system is 10 μm, it is clear that the images of the latter example are less sharp. A definition of resolution that is more in line with the perceived quality, would instead use the spatial frequency at which the first zero occurs. Definitions of resolution, even for perfect imaging systems, vary widely. A more complete, unambiguous picture is provided by the optical transfer function.

The OTF of an optical system with a non-rotational symmetric aberration[edit]

Optical systems, and in particular optical aberrations are not always rotational symmetric. Periodic patterns that have a different orientation can thus be imaged with different contrast even if their periodicity is the same. Optical transfer function or modulation transfer functions are thus generally two-dimensional functions. The following figures shows the two-dimensional equivalent of the ideal and the imperfect system discussed earlier, next to an optical system with coma, a non-rotational-symmetric aberration.

Optical transfer functions are not always real-valued. Period patterns can be shifted by any amount, depending on the aberration in the system. This is generally the case with non-rotational-symmetric aberrations. The hue of the colors of the surface plots in the above figure indicate phase. It can be seen that, while for the rotational symmetric aberrations the phase is either 0 or π and thus the transfer function is real valued, for the non-rotational symmetric aberration the transfer function has an imaginary component and the phase varies continuously.

Relationship with other metrics[edit]

The optical transfer function has a close relationship with various commonly used metrics to characterize imaging systems. In contrast to other metrics, the optical transfer function does not characterize an imaging system with a single number, it specifies a value for the whole spatial frequency spectrum. This section discusses the parallels it has with several important metrics.

Resolution[edit]

Consider three lens systems: a perfect high resolution lens, a perfect low resolution lens, and an imperfect (aberrated) high resolution lens. The absolute value of the respective optical transfer functions could look as given in the following figures:

// Figure:  //

The finite extent of the optical transfer function reflects a well-defined limit on resolution. The contrast is zero for spatial frequencies above this cut-off. Without prior knowledge of the objects under investigation, it is not possible to resolve features smaller than the period of the cut-off spatial frequency. The resolution of an imaging system could thus be defined as the reciprocal of this cut-off, as was done by Abbe when determining the resolution limit of a microscope. Other metrics for resolution are the full-width at half-maximum (FWHM) of the point-spread function and the Hopkins criterion, both of which yield comparable figures when the optical system is not aberrated.

Note that various super resolution techniques exploit or introduce prior knowledge into the to-be-imaged object, e.g. by assuming that light is only emitted from discrete point emitters such as fluorophores, or by spatially varying illumination with or without saturation. However, in general the resolution limit of an optical imaging system is dictated by the optical transfer function.

Pixel spacing or pixel pitch[edit]

Perhaps with the exception of microscopes, optical imaging systems are often limited by the number of pixels on the sensor, or more specifically, the spacing between these pixels, the pixel pitch. The Nyquist–Shannon theorem states that this pitch should be smaller than half the period of the highest spatial frequency. The main consequence of wider spacing is a reduction in resolution; however, in certain situations also aliasing may cause an important further degradation of the image fidelity.

Pixel size and shape[edit]

The Pixel transfer function (PiTF).

Contrast and practically achievable resolution[edit]

The contrast reduction of a sine pattern as imaged by an optical system is given by its modulation transfer function (MTF). Other period patterns, such as black and white stripes, may have a slightly different contrast; however, when the MTF is known, the contrast of other periodic patterns can be determined as a weighted sum of multiple values of the MTF. The frequencies and weights are given by the components in the Fourier transform of the square wave pattern of the black and white stripes.

Note: Shannon, one can transmit under the noise level.

Strehl Intensity Ratio[edit]

The Strehl intensity ratio is an image quality metric that scores a given system with respect to the ideal, diffraction limited, system. In a non-digital imaging system the peak intensity of a point source will always be brightest for a diffraction limited imaging system. The Strehl ratio of an optical system is simply the peak intensity of its point source image, normalized to that of the diffraction limited system.

Since the optical transfer function is based on the point spread function, the image of a point source, the Strehl ratio could be determined from a non-normalized optical transfer function. Typically the Strehl ratio is used to indicate modest deviations from the ideal system. In that case the point of maximum intensity will not change position, the total transmission will be comparable, and the Strehl ratio will be approximately equal to the integral of the optical transfer function of the system under investigation divided by that of the diffraction limited system.

Calculation[edit]

Most optical design software has functionality to compute the optical or modulation transfer function of a lens design. Ideal systems such as in the examples here are readily calculated numerically using software such as GNU Octave or Matlab, and in specific cases even analytically. The optical transfer function can be calculate using two methods^[1]:

as the Fourier transform of the incoherent point spread function, or
as the auto-correlation of the pupil function of the optical system

Mathematically both approaches are equivalent. Numeric calculations are typically most efficiently done via the Fourier transform; however, analytic calculation may be more tractable using the auto-correlation approach.

In microscopy it is often useful to consider the vectorial OTF. ^[2]

File:Mtf3D.svg

The three-dimensional optical-transfer function. Color coded magnitudes are shown on logarithmic scale.

Examples[edit]

The optical transfer function of two optical designs is now calculated using both approaches. As a first design we consider the

Ideal lens system with circular aperture[edit]

Fourier transform of the point spread function[edit]

Note: Nyquist sampling required!

Auto-correlation of the pupil function[edit]

Since the optical transfer function is the Fourier transform of the point spread function, and the point spread function is the square absolute of the inverse Fourier transformed pupil function, the optical transfer function can also be calculated directly from the pupil function. From the Convolution theorem it can be seen that the optical transfer function is in fact the auto-correlation of the pupil function.

The pupil function of an ideal optical system with a circular aperture is a disk of unit radius. The optical transfer function of such a system can thus be calculated geometrically from the intersecting area between two identical disks at a distance of $2\nu$ , where $\nu$ is the spatial frequency normalized to the highest transmitted frequency. In general the optical transfer function is normalized to a maximum value of one for $\nu =0$ , so the resulting area should be divided by $\pi$ .

The intersecting area can be calculated as the sum of that of two identical Circular segments: $\theta /2-\sin(\theta )/2$ , where $\theta$ is the circle segment angle. By substituting $\nu =cos(\theta /2)$ , and using the equalities $\sin(\theta )/2=\sin(\theta /2)\cos(\theta /2)$ and $1=\nu ^{2}+\sin(\arccos(\nu ))^{2}$ , this can be rewritten as $\arccos(\nu )-\nu {\sqrt {1-\nu ^{2}}}$ . Hence the normalized optical transfer function is given by: $OTF(\nu )={\frac {2}{\pi }}\left(\arccos(\nu )-\nu {\sqrt {1-\nu ^{2}}}\right)$

Ideal reflective telescope with central obscuration[edit]

Reflecting telescopes such as the Cassegrain reflector consist of a large curved mirror that reflects the star light onto a smaller secondary mirror that directs it toward the detector array or photographic film. It can be noticed that a large fraction of the light is blocked by the back of the secondary mirror. Hence, the pupil function of this reflecting telescope will be zero at the center, corresponding to the annular aperture. To keep the example as simple as possible, it is assumed that the pupil function is zero up to half the radius and unity elsewhere in the circular aperture.

Fourier transform[edit]

Auto-correlation[edit]

Measurement[edit]

The optical transfer function is not only useful for the design of optical system, it is also valuable to characterize manufactured systems.

Via the point spread function[edit]

The optical transfer function is defined as the Fourier transform of the impulse-response of the optical system, also called the point spread function. The optical transfer function is thus readily obtained by first acquiring the image of an incoherent point source, and applying the two-dimensional discrete Fourier transform to the sampled image. Such a point-source can, for example, be a bright light behind a screen with a pin hole, a fluorescent or metallic microsphere, or simply a dot painted on a screen. Calculation of the optical transfer function via the point spread function is versatile as it can fully characterize optics with spatial varying and chromatic aberrations by repeating the procedure for various positions and wavelength spectra of the point source.

Extended test objects for spatially invariant optics[edit]

When the aberrations can be assumed to be spatially invariant, alternative patterns can be used to determine the optical transfer function such as lines and edges. The corresponding transfer functions are referred to as the line-spread function and the edge-spread function, respectively. Such extended objects illuminate more pixels in the image, and can improve the measurement accuracy due to the larger signal-to-noise ratio. The optical transfer function is in this case calculated as the two-dimensional discrete Fourier transform of the image and divided by that of the extended object. Typically either a line or a black-white edge is used.

Via the line-spread function[edit]

The two-dimensional Fourier transform of a line through the origin, is a line orthogonal to it and through the origin. The divisor is thus zero for all but a single dimension, by consequence, the optical transfer function can only be determined for a single dimension using a single line-spread function. If necessary, the two-dimensional optical transfer function can be determined by repeating the measurement with lines at various angles.

Via the edge-spread function[edit]

The two-dimensional Fourier transform of an edge is also only non-zero on a single line, orthogonal to the edge. However, the values on this line are inversely proportional to the distance from the origin. Although the measurement images obtained with this technique illuminate a large area of the camera, this mainly benefits the accuracy at low spatial frequencies. As with the line spread function, each measurement only determines a single axes of the optical transfer function, repeated measurements are thus necessary if the optical system cannot be assumed rotational symmetric.

Limitations[edit]

Incoherent only
Spatial invariance required, at least locally: plenoptic camera not.

References[edit]

^ Goodman, Joseph (2005). Introduction to Fourier Optics (3rd ed, ed.). Roberts & Co Publishers. ISBN 0-9747077-2-4.{{cite book}}: CS1 maint: extra punctuation (link)
^ Arnison, M. R.; Sheppard, C. J. R. (2002). "A 3D vectorial optical transfer function suitable for arbitrary pupil functions". Optics Communications. 211: 53. doi:10.1016/S0030-4018(02)01857-6.

[Goodman2005-1] Goodman, Joseph (2005). Introduction to Fourier Optics (3rd ed, ed.). Roberts & Co Publishers. ISBN 0-9747077-2-4.{{cite book}}: CS1 maint: extra punctuation (link)

[Arnison2002-2] Arnison, M. R.; Sheppard, C. J. R. (2002). "A 3D vectorial optical transfer function suitable for arbitrary pupil functions". Optics Communications. 211: 53. doi:10.1016/S0030-4018(02)01857-6.

[1]

[2]