Mathematical fallacy

In mathematics, there are a variety of spurious proofs of obvious contradictions. Although the proofs are flawed, the errors, usually by design, are comparatively subtle. These fallacies are normally regarded as mere curiosities, but can be used to show the importance of rigor in mathematics.

Power and root manipulation

Proof that 1 = −1

Version 1

Start with the identity

$-1=-1\,$

Convert both sides of the equation into the vulgar fractions

${\frac {1}{-1}}={\frac {-1}{1}}$

Apply square roots on both sides to yield

${\sqrt {\frac {1}{-1}}}={\sqrt {\frac {-1}{1}}}$

${\frac {\sqrt {1}}{\sqrt {-1}}}={\frac {\sqrt {-1}}{\sqrt {1}}}$

Multiply both sides by ${\sqrt {1}}\cdot {\sqrt {-1}}$ to obtain

${\sqrt {1}}\cdot {\sqrt {1}}={\sqrt {-1}}\cdot {\sqrt {-1}}$

Any number's square root squared gives the original number, so

$\displaystyle {1=-1}$

Q.E.D.

The proof is invalid because it applies the following principle for square roots incorrectly:

${\sqrt {\frac {x}{y}}}={\frac {\sqrt {x}}{\sqrt {y}}}$

This is only true when x and y are positive real numbers, which is not the case in the proof above. Thus, the proof is invalid.

Version 2

By incorrectly manipulating radicals, the following invalid proof is derived:

$1={\sqrt {1}}={\sqrt {(-1)(-1)}}={\sqrt {-1}}{\sqrt {-1}}=-1$

Q.E.D.

The rule ${\sqrt {xy}}={\sqrt {x}}{\sqrt {y}}$ is generally valid only if at least one of the two numbers x or y is positive, which is not the case here. Alternatively, one can view the square root as a 2-valued function over the complex numbers; in this case both sides of the above equation evaluate to {1, -1}.

Version 3

By crossing into and out of the realm of complex numbers, the following invalid proof is derived:

$-1=(-1)^{3}=(-1)^{\frac {6}{2}}=((-1)^{6})^{\frac {1}{2}}=1^{\frac {1}{2}}=1$

Q.E.D.

The equation $a^{bc}=(a^{b})^{c}$, when b and/or c are fractions, is generally valid only when a is positive, which is not the case here, leading to an invalid proof.

Version 4

Start with the Pythagorean identity

$\,\cos ^{2}x=1-\sin ^{2}x$

Raise both sides of the equation to the 3/2 power to obtain

$(\cos ^{2}x)^{\frac {3}{2}}=(1-\sin ^{2}x)^{\frac {3}{2}}$

$(\cos ^{3}x)=(1-\sin ^{2}x)^{\frac {3}{2}}$

Let $x=\pi$

$-1=(1-0)^{\frac {3}{2}}$

$-1=1\,$

Q.E.D.

In this proof, the fallacy is in the third step, where the rule $(a^{b})^{c}=a^{bc}$ is applied without ensuring that a is positive.

Proof that x=y for any real x, y

If $a^{b}=a^{c}$ then $b=c$. Therefore, since $1^{x}=1^{y}$, we may deduce $x=y$.

Q.E.D.

The error in this proof lies in the fact that the stated rule is true only for positive $a\neq 1$.

Division by zero

Proof that 2 = 1

Let a and b be equal non-zero quantities

$a=b\,$

Multiply through by a

$a^{2}=ab\,$

Subtract $b^{2}\,$

$a^{2}-b^{2}=ab-b^{2}\,$

Factor both sides

$(a-b)(a+b)=b(a-b)\,$

Divide out $(a-b)\,$

$a+b=b\,$

Observing that $a=b\,$

$b+b=b\,$

Combine like terms on the left

$2b=b\,$

Divide by the non-zero b

$2=1\,$

Q.E.D.

The fallacy is in line 5: the progression from line 4 to line 5 involves division by $(a-b)$, which is zero since a equals b. Since division by zero is undefined, the argument is invalid. Deriving that the only possible solution for lines 5, 6, and 7, namely that $a=b=0$, this flaw is evident again in line 7, where one must divide by b (0) in order to produce the fallacy (not to mention that the only possible solution denies the original premise that a and b are nonzero). A similar invalid proof would be to say that $2(0)=1(0)$ (which is true) therefore, by dividing by zero, $2=1$.

Proof that all numbers are equal to 1

Suppose we have the following system of linear equations:

$\left\{{\begin{matrix}c_{1}x_{1}+c_{1}x_{2}+\dots +c_{1}x_{n}=c_{1}\\c_{2}x_{1}+c_{2}x_{2}+\dots +c_{2}x_{n}=c_{2}\\\vdots \\c_{n}x_{1}+c_{n}x_{2}+\dots +c_{n}x_{n}=c_{n}\end{matrix}}\right.$

Dividing the first equation by $c_{1}$, we get $x_{1}+x_{2}+\dots +x_{n}=1.$ Let us now try to solve the system via Cramer's rule:

${\begin{bmatrix}c_{1}&c_{1}&c_{1}&\dots \\c_{2}&c_{2}&c_{2}&\dots \\\vdots &\vdots &\vdots &\\c_{n}&c_{n}&c_{n}&\dots \end{bmatrix}}{\begin{bmatrix}x_{1}\\x_{2}\\\vdots \\x_{n}\end{bmatrix}}={\begin{bmatrix}c_{1}\\c_{2}\\\vdots \\c_{n}\end{bmatrix}}$

Since each column of the coefficient matrix is equal to the resultant column vector, we have

$A_{i}=A\implies |A_{i}|=|A|\implies {|A_{i}| \over |A|}=1=x_{i}$

for all $i$. Substituting this back into $x_{1}+x_{2}+\dots +x_{n}=1$, we get

$\sum _{i=1}^{n}i=1$.

Q.E.D.

This proof is fallacious because Cramer's rule can only be applied to systems with a unique solution; however, all the equations in the system are obviously equivalent, and insufficient to provide a unique solution. The fallacy occurs when we try to divide $|A_{i}|$ by $|A|$, as both are equal to 0.

Calculus

Proof that 2 = 1

By the common intuitive meaning of multiplication we can see that

$4\times 3=3+3+3+3\,$

It can also be seen that for a non-zero x

$x=1_{1}+1_{2}+\cdots +1_{x}$

Now we multiply through by x

$x^{2}=x_{1}+x_{2}+\cdots +x_{x}$

Then we take the derivative with respect to x

$2x=1_{1}+1_{2}+\cdots +1_{x}$

Now we see that the right hand side is x which gives us

$2x=x\,$

Finally, dividing by our non-zero x we have

$2=1\,$

Q.E.D.

The fallacy lies in line two. Our definition of x assumed that x was an integer; this equation is not meaningful for non-integer real numbers. Functions are only differentiable on a continuous space such as the real numbers, not on integers. For any particular integer x, you get a true equation. But to differentiate both sides you need an equation of functions, not an equation of integers. The right-hand function $x+x+\cdots +x$ with x terms is not a meaningful function on the reals and thus not differentiable.

Also, when taking the derivative in line 4 the derivative is taken with respect to each of the terms individually, but not with respect to the numbers of terms. This is erroneous, as the number of terms is x, the variable of differentiation. The chain rule is incorrectly not applied on the right-hand side of the equation.

Proof that 0 = 1

Begin with the evaluation of the indefinite integral

$\int {\frac {1}{x}}dx$

Through integration by parts, let

$u={\frac {1}{x}}$ and $dv=dx$

Thus,

$du=-{\frac {1}{x^{2}}}dx$ and $v=x$

Hence, by integration by parts

$\int {\frac {1}{x}}dx={\frac {x}{x}}-\int \left(-{\frac {1}{x^{2}}}\right)xdx$

$\int {\frac {1}{x}}dx=1+\int {\frac {1}{x}}dx$

$0=1\,$

Q.E.D.

The error in this proof lies in an improper use of the integration by parts technique. Upon use of the formula, a constant, C, must be added to the right-hand side of the equation. This is due to the derivation of the integration by parts formula; the derivation involves the integration of an equation and so a constant must be added. In most uses of the integration by parts technique, this initial addition of C is ignored until the end when C is added a second time. However, in this case, the constant must be added immediately because the remaining two integrals cancel each other out.

In other words, the second to last line is correct (1 added to any antiderivative of 1/x is still an antiderivative of 1/x); but the last line is not. You cannot cancel $\int 1/x\,dx$ because they are not necessarily equal. There are infinitely many antiderivatives of a function, all differing by a constant. In this case, the antiderivatives on both sides differ by 1.

This problem can be avoided if we use definite integrals (i.e. use bounds). Then in the second to last line, 1 would be evaluated between some bounds, which would always evaluate to 1 - 1 = 0. The remaining definite integrals on both sides would indeed be equal.

Proof that 1 = 0

Take the statement

$x=1\,$

Taking the derivative of each side,

${\frac {d}{dx}}x={\frac {d}{dx}}1$

The derivative of x is 1, and the derivative of 1 is 0. Therefore,

$1=0\,$

Q.E.D.

The error in this proof is that derivatives are only applicable to functions. Also, since x is assinged a real number value, then x would be a constant, and the derivative of a constant is zero, therefore making the correct identity 0 = 0.

Infinite series

Proof that 0 = 1

Start with the addition of an infinite succession of zeros

$0=0+0+0+\cdots$

Then recognize that $0=1-1$

$0=(1-1)+(1-1)+(1-1)+\cdots$

Applying the associative law of addition results in

$0=1+(-1+1)+(-1+1)+(-1+1)+\cdots$

Of course $-1+1=0$

$0=1+0+0+0+\cdots$

And the addition of an infinite string of zeros can be discarded leaving

$0=1\,$

Q.E.D.

The error here is that the associative law cannot be applied freely to an infinite sum unless the sum would converge without any parentheses. Here that sum is 1 − 1 + 1 − 1 + · · ·, a classic divergent series. In this particular argument, the second line gives the sequence of partial sums 0, 0, 0, ... (which converges to 0) while the third line gives the sequence of partial sums 1, 1, 1, ... (which converges to 1), so these expressions need not be equal. This can be seen as a counterexample to generalizing Fubini's theorem and Tonelli's theorem to infinite integrals (sums) over measurable functions taking negative values.

Proof that a series of positive terms sums to −1

Main article: 1 + 2 + 4 + 8 + · · ·

Start with the infinite geometric series

$1+2+4+8+\cdots$

The well-known formula for the sum of an infinite geometric series is

${\frac {a_{0}}{1-r}}$

where a₀ is the first term of the series and r is the common ratio between terms. Applying this formula yields

$1+2+4+8+\cdots ={\frac {1}{1-2}}=-1$

Q.E.D.

The error in this proof lies in the fact that a geometric series converges if and only if $|r|<1$.

Extraneous solutions

Proof that −2 = 1

Start by attempting to solve the equation

${\sqrt[{3}]{1-x}}+{\sqrt[{3}]{x-3}}=1\,$

Taking the cube of both sides yields

$(1-x)+3{\sqrt[{3}]{1-x}}\ {\sqrt[{3}]{x-3}}\ ({\sqrt[{3}]{1-x}}+{\sqrt[{3}]{x-3}})+(x-3)=1\,$

Replacing the expression within parenthesis by the initial equation and canceling common terms yields

$-2+3{\sqrt[{3}]{1-x}}\ {\sqrt[{3}]{x-3}}=1\,$

${\sqrt[{3}]{1-x}}\ {\sqrt[{3}]{x-3}}=1\,$

Taking the cube again produces

$(1-x)(x-3)=1\,$

$-x^{2}+4x-3=1\,$

$x^{2}-4x+4=0\,$

Which produces the solution x = 2. Substituting this value into the original equation, one obtains

${\sqrt[{3}]{1-2}}+{\sqrt[{3}]{2-3}}=1\,$

So therefore

$(-1)+(-1)=1\,$

$-2=1\,$

Q.E.D.

The fallacy here is that an equation altered by raising both sides to a power is a consequence, but not necessarily equivalent to, the original equation, so it may produce more solutions. This is indeed the case in this example, where the solution x = 2 is arrived at while it is clear that this is not a solution to the original equation. Also, every number has 3 cube roots, 2 complex and one either real or complex. So X=2 may work for the complex root.

Proof that 3 = 0

Assume the following equation for a complex x :

$x^{2}+x+1=0\,$

Then:

$x^{2}=-x-1\,$

Divide by x (assume x is not 0)

$x=-1-1/x\,$

Substituting the last expression for x in the original equation we get:

$x^{2}+(x)+1=0\,$

$x^{2}+(-1-1/x)+1=0\,$

$x^{2}+(-1/x)=0\,$

$x^{2}=1/x\,$

$x^{3}=1\,$

$x=1\,$

Substituting x=1 in the original equation yields:

$1^{2}+1+1=0\,$

$3=0\,$

Q.E.D.

The fallacy here is in assuming that $x^{3}=1$ implies $x=1$. There are in fact three cubed roots of unity.

Complex numbers

Proof that 1 = 3

From Euler's formula we see that

$e^{\pi i}=\cos(\pi )+i\sin(\pi )=-1+0i=-1\,$

and

$e^{3\pi i}=\cos(3\pi )+i\sin(3\pi )=-1+0i=-1\,$

so we have

$e^{\pi i}=e^{3\pi i}\,$

Taking logarithms gives

$\ln(e^{\pi i})=\ln(e^{3\pi i})\,$

and hence

$\pi i={3\pi i}\,$

Dividing by πi gives

$1=3\,$

QED.

The mistake is that the rule $\ln(e^{x})=x$ is in general only valid for real x, not for complex x. The complex logarithm is actually multi-valued; and $\ln(-1)=(2k+1)\pi i$ for any integer k, so we see that $\pi i$ and $3\pi i$ are two among the infinite possible values for ln(-1).

Proof that x = y for any real x, y

Let x and y be any two numbers Then let $a=x-y\ ,\ b=(x+y)^{2}\ ,\ c=4(x^{2}-xy+y^{2})\,$ Let $u=a\ ,\ v=b-c\,$ Let's compute:

$(u+{\sqrt {v}})^{3}=u^{3}+3u^{2}{\sqrt {v}}+3uv+v{\sqrt {v}}$

$(u-{\sqrt {v}})^{3}=u^{3}-3u^{2}{\sqrt {v}}+3uv-v{\sqrt {v}}$

Replacing $u=a\ ,\ v=b-c$, we get:

$(a+{\sqrt {b-c}})^{3}=a\ (a^{2}+3b-3c)+(3a^{2}+b-c){\sqrt {b-c}}$

$(a-{\sqrt {b-c}})^{3}=a\ (a^{2}+3b-3c)-(3a^{2}+b-c){\sqrt {b-c}}$

Let's compute $3a^{2}+b-c\,$ Replacing $a=x-y\ ,\ b=(x+y)^{2}\ ,\ c=4(x^{2}-xy+y^{2})\,$:

$3a^{2}+b-c=3(x^{2}-2xy+y^{2})+x^{2}+2xy+y^{2}-4(x^{2}-xy+y^{2})=0\,$

So:

$(a+{\sqrt {b-c}})^{3}=(a-{\sqrt {b-c}})^{3}\,$

$a+{\sqrt {b-c}}=a-{\sqrt {b-c}}\,$

${\sqrt {b-c}}=0\,$

$b-c=0\,$

$b=c\,$

Replacing $b=(x+y)^{2}\ ,\ c=4(x^{2}-xy+y^{2})\,$:

$(x+y)^{2}=4(x^{2}-xy+y^{2})\,$

$x^{2}+2xy+y^{2}=4(x^{2}-xy+y^{2})\,$

$-3x^{2}+6xy-3y^{2}=0\,$

$(x-y)^{2}=0\,$

$x-y=0\,$

$x=y\,$

Q.E.D.

The mistake here is that from z³ = w³ one may not in general deduce z = w (unless z and w are both real, which they are not in our case).

Inequalities

Proof that 1 < 0

Let us first suppose that

$\displaystyle {0<x<1}$

Now we will take the logarithm of both sides. As long as x > 0, we can do this because logarithms are monotonically increasing. Observing that the logarithm of 1 is 0, we get

$\displaystyle {\ln(x)<0}$

Dividing by ln (x) gives

$\displaystyle {1<0}$

Q.E.D.

The violation is found in the last step, the division. This step is invalid because ln(x) is negative for 0 < x < 1. While multiplication or division by a positive number preserves the inequality, multiplication or division by a negative number reverses the inequality, resulting in the correct expression 1 > 0.

Infinity

Proof that ∞ = 1/4

Since an infinitely large plane has the coordinates of (-∞,∞) × (-∞,∞), this means that

${\frac {}{}}\infty =[\infty -(-\infty )]^{2}$

Which can be simplified into

${\frac {}{}}\infty =(2\infty )^{2}$

And finally

${\frac {}{}}\infty =4\infty ^{2}$

Now combine the ∞'s:

$1=4{\frac {\infty ^{2}}{\infty }}$

This itself then simplifies into

$1=4\infty \,$

And finally, to find the value of ∞ itself,

${\frac {1}{4}}=\infty$

This can be checked by starting with the equation given in step 1,

${\frac {}{}}\infty =[\infty -(-\infty )]^{2}$

Substitute in the above value of ∞ to see if it really works:

${\frac {1}{4}}=\left[{\frac {1}{4}}-\left(-{\frac {1}{4}}\right)\right]^{2}$

Which is then simplified to get

${\frac {1}{4}}=\left[{\frac {1}{2}}\right]^{2}$

And that then simplifies into

${\frac {1}{4}}={\frac {1}{4}}$

Q.E.D.

This proof's fallacy is using ∞ (infinity) to represent a finite value – in reality infinity is thought of as a direction as opposed to a destination. One of the more unusual aspects of this type of invalid proof is that it can be checked, unlike many other invalid proofs, particularly ones which rely on division by zero. Also, infinity divided by itself is undefined.

Examples in geometry

Proof that any angle is zero

Diagram for proof that any angle is zero

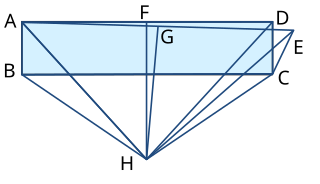
Construct a rectangle ABCD. Now identify a point E such that CD=CE and the angle DCE is a non-zero angle. Take the perpendicular bisector of AD, crossing at F, and the perpendicular bisector of AE, crossing at G. Label where the two perpendicular bisectors intersect as H and join this point to A, B, C, D, and E.

Now, AH=DH because FH is a perpendicular bisector; similarly BH=CH. AH=EH because GH is a perpendicular bisector, so DH=EH. And by construction BA=CD=CE. So the triangles ABH, DCH and ECH are congruent, and so the angles ABH, DCH and ECH are equal.

But if the angles DCH and ECH are equal then the angle DCE must be zero.

Q.E.D.

The error in the proof comes in the diagram and the final point. An accurate diagram would show that the triangle ECH is a reflection of the triangle DCH in the line CH rather than being on the same side, and so while the angles DCH and ECH are equal in magnitude, there is no justification for subtracting one from the other; to find the angle DCE you need to subtract the angles DCH and ECH from the angle of a full circle (2π or 360°).

Proof that any parallelogram has infinite area

Take a parallelogram ABCD. Rule an infinite number of lines equal and parallel to CD along AD's length until ABCD is completely full of these lines. As these lines all equal CD, the total area of these lines (and thus the parallelogram) is ∞ × (CD), thus infinity.

Q.E.D.

The fallacy here is that a line does not represent an area, and can't be used in this way. Also, infinity is not a number and it can't be used in equations.

Proof that any triangle is isosceles

It is sufficient to prove that any two sides of a triangle are congruent.

Refer to the diagrams at MathPages article.

Given a triangle △ABC, proof that AB = AC:

1. Draw a line bisecting ∠A
2. Call the midpoint of line segment BC, D
3. Draw the perpendicular bisector of segment BC, which contains D
4. If these two lines are parallel, AB = AC, by some other theorem; otherwise they intersect at point P
5. Draw line PE perpendicular to AB, line PF perpendicular to AC
6. Draw lines PB and PC
7. By AAS, △EAP ≅ △FAP (AP = AP; ∠PAF ≅ ∠PAE since AP bisects ∠A; ∠AEP ≅ ∠AFP are both right angles)
8. By HL, △PDB ≅ △PDC (∠PDB,∠PDC are right angles; PD = PD; BD = CD because PD bisects BC)
9. By SAS, △EPB ≅ △FPC (EP = FP since △EAP ≅ △FAP; BP = CP since △PDB ≅ △PDC; ∠EPB ≅ ∠FPC since they are vertical angles)
10. Thus, AE ≅ AF, EB ≅ FC, and AB = AE + EB = AF + FC = AC

Q.E.D.

As a corollary, one can show that all triangles are equilateral, by showing that AB = BC and AC = BC in the same way.

All but the last step of the proof is indeed correct (those three triangles are indeed congruent). The error in the proof is the assumption in the diagram that the point P is inside the triangle. In fact, whenever AB ≠ AC, P lies outside the triangle. Furthermore, it can be further shown that, if AB is shorter than AC, then E will lie outside of AB, while F will lie within AC (and vice versa). (Any diagram drawn with sufficiently accurate instruments will verify the above two facts.) Because of this, AB is actually AE - EB, whereas AC is still AF + FC; and thus the lengths are not necessarily the same.

See also

• Paradox
• Fallacy

External links

• More invalid proofs from AhaJokes.com
• More invalid proofs also on this page