Van Aubel's theorem

The theorem can be applied to a complex (self-intersecting) quadrilateral.

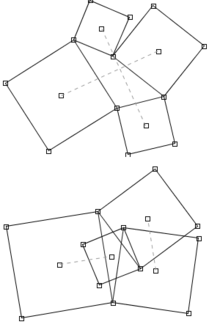
In geometry, Van Aubel's theorem describes a relationship between squares constructed on the sides of a quadrilateral. Starting with a given quadrilateral (a polygon having four sides), construct a square on each side. Van Aubel's theorem holds that the two line segments between the centers of opposite squares are of equal lengths and that the lines through the centers are at right angles to one another. The theorem is named after H. H. van Aubel, who published it in 1878.

See also

• Petr–Douglas–Neumann theorem
• Thébault's theorem
• Napoleon's theorem

External links

• Van Aubel's Theorem: an interactive JavaSketch of the figure.
• Weisstein, Eric W. "van Aubel's Theorem". MathWorld.
• Van Aubel's Theorem for Quadrilaterals and Van Aubel's Theorem for Triangles by Jay Warendorff, The Wolfram Demonstrations Project.
• Van Aubel's Theorem and some generalizations at Dynamic Geometry Sketches