Kosnita's theorem: Difference between revisions
Appearance
Content deleted Content added
No edit summary |
No edit summary |
||
| Line 5: | Line 5: | ||
Let <math>ABC</math> be an arbitrary triangle, <math>O</math> its [[circumcenter]] and <math>O_a,O_b,O_c</math> are the circumcenters of three triangles <math>OBC</math>, <math>OCA</math>, and <math>OAB</math> respectively. The theorem claims that the three [[straight line]]s <math>AO_a</math>, <math>BO_b</math>, and <math>CO_c</math> are concurrent.<ref name=wolframKosnita/> This result has been established by the Romanian mathematician [[Cezar Coşniţă]] (1910-1962).<ref name=patrascu/> |
Let <math>ABC</math> be an arbitrary triangle, <math>O</math> its [[circumcenter]] and <math>O_a,O_b,O_c</math> are the circumcenters of three triangles <math>OBC</math>, <math>OCA</math>, and <math>OAB</math> respectively. The theorem claims that the three [[straight line]]s <math>AO_a</math>, <math>BO_b</math>, and <math>CO_c</math> are concurrent.<ref name=wolframKosnita/> This result has been established by the Romanian mathematician [[Cezar Coşniţă]] (1910-1962).<ref name=patrascu/> |
||
Their point of concurrence is known as the triangle's '''Kosnita point''' (named by Rigby in 1997). It is the [[isogonal conjugate]] of the [[nine-point center]].<ref name=grinberg2003/><ref name=rigby1997/> It is [[triangle center]] <math>X(54)</math> in [[Kimberling center|Clark Kimberling's list]].<ref name=kimberlingX54/> This theorem is special case of [[Dao's theorem on six circumcenters]] associated with a cyclic hexagon in.<ref name=dergiadesDao6CCCH/><ref name=cohlDao6CCCH/><ref name=NgoQuangDuong /><ref name=C.Kimberling/><ref |
Their point of concurrence is known as the triangle's '''Kosnita point''' (named by Rigby in 1997). It is the [[isogonal conjugate]] of the [[nine-point center]].<ref name=grinberg2003/><ref name=rigby1997/> It is [[triangle center]] <math>X(54)</math> in [[Kimberling center|Clark Kimberling's list]].<ref name=kimberlingX54/> This theorem is special case of [[Dao's theorem on six circumcenters]] associated with a cyclic hexagon in.<ref name=dergiadesDao6CCCH/><ref name=cohlDao6CCCH/><ref name=NgoQuangDuong /><ref name=C.Kimberling/><ref> Nguyễn Minh Hà, ''[http://geometry-math-journal.ro/pdf/Volume6-Issue1/4.pdf Another Purely Synthetic Proof of Dao's Theorem on Sixcircumcenters]''. Journal of Advanced Research on Classical and Modern Geometries, ISSN: 2284-5569, volume 6, pages 37–44. {{MR|....}}</ref><ref> Nguyễn Tiến Dũng, ''[http://geometry-math-journal.ro/pdf/Volume6-Issue1/6.pdf A Simple proof of Dao's Theorem on Sixcircumcenters]''. Journal of Advanced Research on Classical and Modern Geometries, ISSN: 2284-5569, volume 6, pages 58–61. {{MR|....}}</ref> |
||
Revision as of 03:21, 7 April 2017
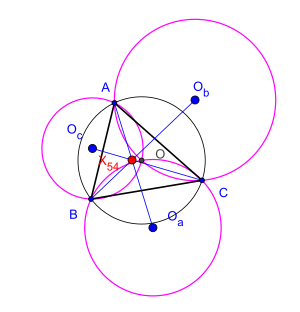
In Euclidean geometry, Kosnita's theorem is a property of certain circles associated with an arbitrary triangle.
Let be an arbitrary triangle, its circumcenter and are the circumcenters of three triangles , , and respectively. The theorem claims that the three straight lines , , and are concurrent.[1] This result has been established by the Romanian mathematician Cezar Coşniţă (1910-1962).[2]
Their point of concurrence is known as the triangle's Kosnita point (named by Rigby in 1997). It is the isogonal conjugate of the nine-point center.[3][4] It is triangle center in Clark Kimberling's list.[5] This theorem is special case of Dao's theorem on six circumcenters associated with a cyclic hexagon in.[6][7][8][9][10][11]
References
- ^ Weisstein, Eric W. "Kosnita Theorem". MathWorld.
- ^ Ion Pătraşcu (2010), A generalization of Kosnita's theorem (in Romanian)
- ^ Darij Grinberg (2003), On the Kosnita Point and the Reflection Triangle. Forum Geometricorum, volume 3, pages 105–111. ISSN 1534-1178
- ^ John Rigby (1997), Brief notes on some forgotten geometrical theorems. Mathematics and Informatics Quarterly, volume 7, pages 156-158 (as cited by Kimberling).
- ^ Clark Kimberling (2014), Encyclopedia of Triangle Centers, section X(54) = Kosnita Point. Accessed on 2014-10-08
- ^ Nikolaos Dergiades (2014), Dao’s Theorem on Six Circumcenters associated with a Cyclic Hexagon. Forum Geometricorum, volume 14, pages=243–246. ISSN 1534-1178.
- ^ Telv Cohl (2014), A purely synthetic proof of Dao's theorem on six circumcenters associated with a cyclic hexagon. Forum Geometricorum, volume 14, pages 261–264. ISSN 1534-1178.
- ^ Ngo Quang Duong, International Journal of Computer Discovered Mathematics, Some problems around the Dao's theorem on six circumcenters associated with a cyclic hexagon configuration, volume 1, pages=25-39. ISSN 2367-7775
- ^ X(3649) = KS(INTOUCH TRIANGLE)
- ^ Nguyễn Minh Hà, Another Purely Synthetic Proof of Dao's Theorem on Sixcircumcenters. Journal of Advanced Research on Classical and Modern Geometries, ISSN: 2284-5569, volume 6, pages 37–44. MR....
- ^ Nguyễn Tiến Dũng, A Simple proof of Dao's Theorem on Sixcircumcenters. Journal of Advanced Research on Classical and Modern Geometries, ISSN: 2284-5569, volume 6, pages 58–61. MR....










