User:Datumizer/Sandbox/Table of fractals: Difference between revisions
Appearance
Content deleted Content added
add example rows |
fix stats |
||
| Line 23: | Line 23: | ||
| [[Cantor set]] || [[File:Cantor set in seven iterations.svg|200px]] || || || || {{tick}} || || || || {{tick}}|| || || <math>\log_3(2)</math> || 0.6309 || || 2 || Built by removing the central third at each iteration. [[Nowhere dense]] and not a [[countable set]]. |
| [[Cantor set]] || [[File:Cantor set in seven iterations.svg|200px]] || || || || {{tick}} || || || || {{tick}}|| || || <math>\log_3(2)</math> || 0.6309 || || 2 || Built by removing the central third at each iteration. [[Nowhere dense]] and not a [[countable set]]. |
||
|- |
|- |
||
| Asymmetric [[Cantor set]] || [[File:AsymmCantor.png|200px]] || {{tick}} || || || || || ||{{tick}} || || || |
| Asymmetric [[Cantor set]] || [[File:AsymmCantor.png|200px]] || {{tick}} || || || || || ||{{tick}} || || || || <math>\log_2(\varphi)=\log_2(1+\sqrt{5})-1</math> || 0.6942 || || 2 || The dimension is not <math>\frac{\ln2}{\ln\frac83}</math>, which is the generalized Cantor set with γ=1/4, which has the same length at each stage.<ref>{{Cite journal|author=Tsang, K. Y. |title=Dimensionality of Strange Attractors Determined Analytically |journal=Phys. Rev. Lett. |volume=57|issue=12|pages=1390–1393 |year=1986|pmid=10033437 |doi=10.1103/PhysRevLett.57.1390|bibcode=1986PhRvL..57.1390T}}</ref> Built by removing the second quarter at each iteration. [[Nowhere dense]] and not a [[countable set]]. <math>\scriptstyle\varphi = \frac{1+\sqrt5}2</math> ([[golden cut]]). |
||
|- |
|- |
||
| [[Real number]]s whose base 10 digits are even || [[File:Even digits.png|200px]] || || || || {{tick}} || || {{tick}} || || || || |
| [[Real number]]s whose base 10 digits are even || [[File:Even digits.png|200px]] || || || || {{tick}} || || {{tick}} || || || || || <math>\log_{10}(5)=1-\log_{10}(2)</math> || 0.69897 || || 2 || Similar to the [[Cantor set]].<ref name="Falconer">{{Cite book | last = Falconer | first = Kenneth | author-link=Kenneth Falconer (mathematician) | title = Fractal Geometry: Mathematical Foundations and Applications | isbn = 978-0-470-84862-3 | no-pp = true | page = xxv}}</ref> |
||
|- |
|- |
||
| Spectrum of Fibonacci Hamiltonian || || || || {{tick}} || || || || || || || || <math> \log(1+\sqrt{2})</math> || 0.88137 || || 2 || The study of the spectrum of the Fibonacci Hamiltonian proves upper and lower bounds for its fractal dimension in the large coupling regime. These bounds show that the spectrum converges to an explicit constant.<ref>{{cite journal |last1=Damanik |first1=D. |last2=Embree |first2=M. |last3=Gorodetski |first3=A. |first4=S. |last4=Tcheremchantse |title=The Fractal Dimension of the Spectrum of the Fibonacci Hamiltonian |journal=Commun. Math. Phys. |volume=280 |issue=2 |pages=499–516 |year=2008 |doi=10.1007/s00220-008-0451-3 |arxiv=0705.0338|bibcode=2008CMaPh.280..499D |s2cid=12245755 }}</ref>{{page needed|date=October 2018}} |
| Spectrum of Fibonacci Hamiltonian || || || || {{tick}} || || || || || || || || <math> \log(1+\sqrt{2})</math> || 0.88137 || || 2 || The study of the spectrum of the Fibonacci Hamiltonian proves upper and lower bounds for its fractal dimension in the large coupling regime. These bounds show that the spectrum converges to an explicit constant.<ref>{{cite journal |last1=Damanik |first1=D. |last2=Embree |first2=M. |last3=Gorodetski |first3=A. |first4=S. |last4=Tcheremchantse |title=The Fractal Dimension of the Spectrum of the Fibonacci Hamiltonian |journal=Commun. Math. Phys. |volume=280 |issue=2 |pages=499–516 |year=2008 |doi=10.1007/s00220-008-0451-3 |arxiv=0705.0338|bibcode=2008CMaPh.280..499D |s2cid=12245755 }}</ref>{{page needed|date=October 2018}} |
||
|- |
|- |
||
| Generalized Cantor set || [[File:generalized cantor set.png|200px]] || || || {{tick}} || || {{tick}} || || || || || |
| Generalized Cantor set || [[File:generalized cantor set.png|200px]] || || || {{tick}} || || {{tick}} || || || || || || <math>\frac{-\log(2)}{\log\left(\displaystyle\frac{1-\gamma}{2}\right)}</math> || 0<D<1 || || 2 || Built by removing at the <math>m</math><sup>th</sup> iteration the central interval of length <math>\gamma\,l_{m-1}</math> from each remaining segment (of length <math>l_{m-1}=(1-\gamma)^{m-1}/2^{m-1}</math>). At <math>\scriptstyle\gamma=1/3</math> one obtains the usual [[Cantor set]]. Varying <math>\scriptstyle\gamma</math> between 0 and 1 yields any fractal dimension <math>\scriptstyle 0\,<\,D\,<\,1</math>.<ref>{{cite journal |first1=A. Yu |last1=Cherny |first2=E.M. |last2=Anitas |first3=A.I. |last3=Kuklin |first4=M. |last4=Balasoiu |first5=V.A. |last5=Osipov |title=The scattering from generalized Cantor fractals |journal=J. Appl. Crystallogr. |volume=43 |issue= 4|pages=790–7 |year=2010 |doi=10.1107/S0021889810014184 |arxiv=0911.2497 |s2cid=94779870 }}</ref> |
||
|} |
|} |
||
Revision as of 19:03, 5 July 2021
| Name | Illustration | Iterated function system | Strange attractor | L-system | Escape-time fractal | Random fractal | Natural fractal | Finite subdivision rule | Exact self-similarity | Quasi-self-similarity | Statistical self-similarity | Hausdorff dimension (exact) | Hausdorff dimension (approx) | Self-similarity dimension | Spatial dimension | Remarks |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Feigenbaum attractor | 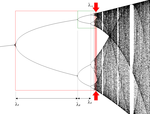 |
Calculated | 0.538 | 2 | The Feigenbaum attractor (see between arrows) is the set of points generated by successive iterations of the logistic function for the critical parameter value , where the period doubling is infinite. This dimension is the same for any differentiable and unimodal function.[1] | |||||||||||
| Cantor set | 0.6309 | 2 | Built by removing the central third at each iteration. Nowhere dense and not a countable set. | |||||||||||||
| Asymmetric Cantor set |  |
0.6942 | 2 | The dimension is not , which is the generalized Cantor set with γ=1/4, which has the same length at each stage.[2] Built by removing the second quarter at each iteration. Nowhere dense and not a countable set. (golden cut). | ||||||||||||
| Real numbers whose base 10 digits are even |  |
0.69897 | 2 | Similar to the Cantor set.[3] | ||||||||||||
| Spectrum of Fibonacci Hamiltonian | 0.88137 | 2 | The study of the spectrum of the Fibonacci Hamiltonian proves upper and lower bounds for its fractal dimension in the large coupling regime. These bounds show that the spectrum converges to an explicit constant.[4][page needed] | |||||||||||||
| Generalized Cantor set |  |
0<D<1 | 2 | Built by removing at the th iteration the central interval of length from each remaining segment (of length ). At one obtains the usual Cantor set. Varying between 0 and 1 yields any fractal dimension .[5] |
- ^ Aurell, Erik (May 1987). "On the metric properties of the Feigenbaum attractor". Journal of Statistical Physics. 47 (3–4): 439–458. Bibcode:1987JSP....47..439A. doi:10.1007/BF01007519. S2CID 122213380.
- ^ Tsang, K. Y. (1986). "Dimensionality of Strange Attractors Determined Analytically". Phys. Rev. Lett. 57 (12): 1390–1393. Bibcode:1986PhRvL..57.1390T. doi:10.1103/PhysRevLett.57.1390. PMID 10033437.
- ^ Falconer, Kenneth. Fractal Geometry: Mathematical Foundations and Applications. xxv. ISBN 978-0-470-84862-3.
- ^ Damanik, D.; Embree, M.; Gorodetski, A.; Tcheremchantse, S. (2008). "The Fractal Dimension of the Spectrum of the Fibonacci Hamiltonian". Commun. Math. Phys. 280 (2): 499–516. arXiv:0705.0338. Bibcode:2008CMaPh.280..499D. doi:10.1007/s00220-008-0451-3. S2CID 12245755.
- ^ Cherny, A. Yu; Anitas, E.M.; Kuklin, A.I.; Balasoiu, M.; Osipov, V.A. (2010). "The scattering from generalized Cantor fractals". J. Appl. Crystallogr. 43 (4): 790–7. arXiv:0911.2497. doi:10.1107/S0021889810014184. S2CID 94779870.














