Torsion constant

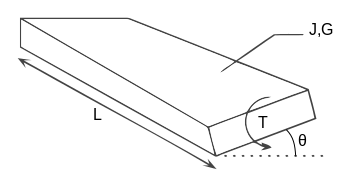
The torsion constant is a geometrical property of a bar's cross-section which is involved in the relationship between angle of twist and applied torque along the axis of the bar, for a homogeneous linear-elastic bar. The torsion constant, together with material properties and length, describes a bar's torsional stiffness. The SI unit for torsion constant is m⁴.

History

In 1820, the French engineer A. Duleau derived analytically that the torsion constant of a beam is identical to the second moment of area normal to the section J_zz, which has an exact analytic equation, by assuming that a plane section before twisting remains planar after twisting, and a diameter remains a straight line. Unfortunately, that assumption is correct only in beams with circular cross-sections, and is incorrect for any other shape where warping takes place.

For non-circular cross-sections, there are no exact analytical equations for finding the torsion constant. However, approximate solutions have been found for many shapes. Non-circular cross-sections always have warping deformations that require numerical methods to allow for the exact calculation of the torsion constant.

The torsional stiffness of beams with non-circular cross sections is significantly increased if the warping of the end sections is restrained by, for example, stiff end blocks.

Partial Derivation

For a beam of uniform cross-section along its length:

$\theta ={\frac {TL}{GJ}}$

where

$\theta$ is the angle of twist in radians

T is the applied torque

L is the beam length

G is the Modulus of rigidity (shear modulus) of the material

J is the torsional constant

Torsional Rigidity (GJ) and Stiffness (GJ/L)

Inverting the previous relation, we can define two quantities: the torsional rigidity,

$GJ={\frac {TL}{\theta }}$ with SI units N⋅m²/rad

And the torsional stiffness,

${\frac {GJ}{L}}={\frac {T}{\theta }}$ with SI units N⋅m/rad

Examples for specific uniform cross-sectional shapes

Circle

$J_{zz}=J_{xx}+J_{yy}={\frac {\pi r^{4}}{4}}+{\frac {\pi r^{4}}{4}}={\frac {\pi r^{4}}{2}}$

where

r is the radius

This is identical to the second moment of area J_zz and is exact.

alternatively write: $J={\frac {\pi D^{4}}{32}}$ where

D is the Diameter

Ellipse

$J\approx {\frac {\pi a^{3}b^{3}}{a^{2}+b^{2}}}$

where

a is the major radius

b is the minor radius

Square

$J\approx \,2.25a^{4}$

where

a is half the side length.

Rectangle

$J\approx \beta ab^{3}$

where

a is the length of the long side

b is the length of the short side

$\beta$ is found from the following table:

a/b	$\beta$
1.0	0.141
1.5	0.196
2.0	0.229
2.5	0.249
3.0	0.263
4.0	0.281
5.0	0.291
6.0	0.299
10.0	0.312
$\infty$	0.333

Alternatively the following equation can be used with an error of not greater than 4%:

$J\approx ab^{3}\left({\frac {16}{3}}-{3.36}{\frac {b}{a}}\left(1-{\frac {b^{4}}{12a^{4}}}\right)\right)$

Note that in this formula, the value for a is half of the length of the long side and b is half of the length of the short side.

Thin walled open tube of uniform thickness

$J={\frac {1}{3}}Ut^{3}$

t is the wall thickness

U is the length of the median boundary (perimeter of median cross section

Circular thin walled open tube of uniform thickness

This is a tube with a slit cut longitudinally through its wall. Using the formula above:

$U=2\pi r$

$J={\frac {2}{3}}\pi rt^{3}$

t is the wall thickness

r is the mean radius

External links

• Torsion constant calculator