Rhombic dodecahedron

Rhombic dodecahedron
(Click here for rotating model)
Type	Catalan solid
Coxeter diagram
Conway notation	jC
Face type	V3.4.3.4 rhombus
Faces	12
Edges	24
Vertices	14
Vertices by type	8{3}+6{4}
Symmetry group	Oh, B3, [4,3], (*432)
Rotation group	O, [4,3]+, (432)
Dihedral angle	120°
Properties	convex, face-transitive isohedral, isotoxal, parallelohedron
Cuboctahedron (dual polyhedron)	Net

The rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.

Properties

It is the polyhedral dual of the cuboctahedron, and a zonohedron. The long diagonal of each face is exactly √2 times the length of the short diagonal, so that the acute angles on each face measure cos⁻¹(1/3), or approximately 70.53°.

Being the dual of an Archimedean polyhedron, the rhombic dodecahedron is face-transitive, meaning the symmetry group of the solid acts transitively on the set of faces. In elementary terms, this means that for any two faces A and B there is a rotation or reflection of the solid that leaves it occupying the same region of space while moving face A to face B.

The rhombic dodecahedron is one of the nine edge-transitive convex polyhedra, the others being the five Platonic solids, the cuboctahedron, the icosidodecahedron and the rhombic triacontahedron.

Part of a Rhombic dodecahedral honeycomb

The rhombic dodecahedron can be used to tessellate 3-dimensional space. It can be stacked to fill a space much like hexagons fill a plane.

This tessellation can be seen as the Voronoi tessellation of the face-centred cubic lattice. Some minerals such as garnet form a rhombic dodecahedral crystal habit. Honeybees use the geometry of rhombic dodecahedra to form honeycomb from a tessellation of cells each of which is a hexagonal prism capped with half a rhombic dodecahedron.

In a perfect vertex-first projection two of the tesseracts vertices (marked in gold) are projected exactly in the center of the rhombic dodecahedron

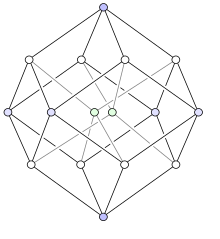
The rhombic dodecahedron forms the hull of the vertex-first projection of a tesseract to 3 dimensions. There are exactly two ways of decomposing a rhombic dodecahedron into 4 congruent parallelepipeds, giving 8 possible parallelepipeds. The 8 cells of the tesseract under this projection map precisely to these 8 parallelepipeds.

Area and volume

The area A and the volume V of the rhombic dodecahedron of edge length a are:

$A=8{\sqrt {2}}a^{2}\approx 11.3137085a^{2}$

$V={\frac {16}{9}}{\sqrt {3}}a^{3}\approx 3.07920144a^{3}$

Cartesian coordinates

The eight vertices where three faces meet at their obtuse angles have Cartesian coordinates

(±1, ±1, ±1)

The six vertices where four faces meet at their acute angles are given by the permutations of

(0, 0, ±2)

See also

• Dodecahedron
• Rhombic triacontahedron
• Truncated rhombic dodecahedron
• 24-cell - 4D analog of rhombic dodecahedron
• Rhombic dodecahedral honeycomb

References

• Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. (Section 3-9)

External links

• Weisstein, Eric W., "Rhombic dodecahedron" ("Catalan solid") at MathWorld.
• Virtual Reality Polyhedra – The Encyclopedia of Polyhedra

Computer models

• Rhombic Dodecahedron -- interactive 3-d model
• Relating a Rhombic Triacontahedron and a Rhombic Dodecahedron, Rhombic Dodecahedron 5-Compound and Rhombic Dodecahedron 5-Compound by Sándor Kabai, The Wolfram Demonstrations Project.

Paper projects

• Rhombic Dodecahedron Calendar – make a rhombic dodecahedron calendar without glue
• Another Rhombic Dodecahedron Calendar – made by plaiting paper strips

Practical applications

• Archimede Institute Examples of actual housing construction projects using this geometry