Minifloat

Minifloats are floating point values represented with very few bits. They are not well suited for numerical calculations. They are used for special purposes like computer graphics, and are useful in computer courses to demonstrate the properties of floating point arithmetic and IEEE 754 numbers.

Minifloats with 16 bits are half-precision numbers (opposed to single and double precision). There are also minifloats with 8 bits or even less.

Minifloats can be designed following the principles of the IEEE 754 standard. In this case they must obey the (not explicitly written) rules for the frontier between subnormal and normal numbers and they must have special patterns for infinite and NaN. Normalized numbers are stored with a biased exponent. The future revision IEEE 754r of the standard will have minifloats with 16 bit.

In the G.711 standard for audio companding designed by ITU-T the data encoding with the A-law essentially encodes a 13 bit signed integer as a 1.3.4 minifloat.

In computer graphics minifloats are sometimes used to represent only integral values. If at the same time subnormal values should exist, the least subnormal number has to be 1. This statement can be used to calculate the bias value. The following example demonstrates the calculation as well as the underlying principles.

Example

A Minifloat in one byte (8 bit) with 1 sign, 4 exponent bit and 3 mantissa bit (in short a 1.4.3.-2 minifloat) should be used to represent integral values. All IEEE 754 principles should be valid. The only free value is the bias, which will come out as -2. The unknown exponent is called for the moment x.

Numbers in a different base are marked as ...(base). Example 101(2) = 5. The bit patterns have spaces to visualize its parts.

Representation of zero

0 0000 000 = 0

Subnormal numbers

The mantissa is extended with 0.:

0 0000 001 = 0.001(2) * 2^x = 0.125 * 2^x = 1 (least subnormal number)
...
0 0000 111 = 0.111(2) * 2^x = 0.875 * 2^x = 7 (greatest subnormal number)

Normalized numbers

The mantissa is extended with 1.:

0 0001 000 = 1.000(2) * 2^x = 1 * 2^x = 8 (least normalized number)
0 0001 001 = 1.001(2) * 2^x = 1.125 * 2^x = 9
...
0 0010 000 = 1.000(2) * 2^(x+1) = 1 * 2^(x+1) = 16 = 1.6e1
0 0010 001 = 1.001(2) * 2^(x+1) = 1.125 * 2^(x+1) = 18 = 1.8e1
...
0 1110 000 = 1.000(2) * 2^(x+13) =  1.000 * 2^(x+13) =  65536 = 6.5e4
0 1110 001 = 1.001(2) * 2^(x+13) =  1.125 * 2^(x+13) =  73728 = 7.4e4
...
0 1110 110 = 1.110(2) * 2^(x+13) =  1.750 * 2^(x+13) = 114688 = 1.1e5
0 1110 111 = 1.111(2) * 2^(x+13) =  1.875 * 2^(x+13) = 122880 = 1.2e5 (greatest normalized number)

(The values on the right are rounded because there is no way to represent a number with five decimal digits in three bits. The second value from the right is the theoretical exact value.)

Infinite

0 1111 000 = infinite

Without the interpretation of IEEE 754 the value would be

0 1111 000 = 1.000(2) * 2^(x+14) =  2^17 = 131072 = 1.3e5

Not a Number

0 1111 xxx = NaN

Without the interpretation of IEEE 754 the value of the greatest NaN would be

0 1111 111 = 1.111(2) * 2^(x+14) =  1.875 * 2^17 = 245760 = 2.5e5

Value of the bias

If the least subnormal value (second line above) should be 1, the value of x has to be x = 3. Therefore the bias has to be -2, that is every stored exponent has to be decreased by -2 or has to be increased by 2, to get the numerical exponent.

Properties of this example

Graphical representation of integral (1.4.3.-2) minifloats.

Integral minifloats in one byte have a greater range of -122880..122880 than twos complement integer with a range -128 .. 127. The greater range is compensated by a poor precision, because there are only 4 mantissa bits or slightly more than one decimal place.

There are only 242 different values (if +0 and -0 are regarded as different), because 14 bit patterns are not numbers (NaN).

The values between 0 and 16 have the same bit pattern as minifloat or twos complement integer. The first pattern with a different value is 00010001, which is 18 as a minifloat and 17 as a twos complement integer.

This coincidence is false for negative values, because floating point values are normally represented in signed magnitude.

The (vertical) real line on the right shows clearly the varying density of the floating point values - a property which is common to any floating point system. This varying density results in a curve, which is similar to the exponential function.

Even many computer scientists not specialized in floating point arithmetic believe that the curve has to be smooth, which is nevertheless not the case. First the curve is not a curve but consists of discrete points though in real floating point systems there are many of them (double has 2^64). Second if you try to connect the points by a smooth curve you will notice, that at points where the value of the exponent changes, this curve has "vertices". Between such "vertices" the curve is linear, i.e. a straight line.

Arithmetic

Addition

Addition of (1.3.2.3)-minifloats.

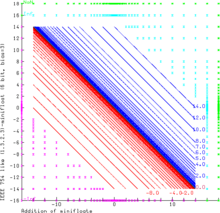
The graphic demonstrates the addition of even smaller (1.3.2.3)-minifloats with 7 bits. This floating point system follows the rules of IEEE 754 exactly. NaN as operand produces always NaN results. Inf - Inf and (-Inf) + Inf results in NaN too (green area). Inf can be augmented and decremented by finite values without change. Sums with finite operands can give an infinite result (i.e. 14.0+3.0 - +Inf as a result is the cyan area, -Inf is the magenta area). The range of the finite operands is filled with the curves x+y=c, where c is always one of the representable float values (blue and red for positive and negative results respectively).

Subtraction, multiplication and division

The other arithmetic operations can be illustrated similarly:

• 
  Subtraction
• 
  Multiplication
• 
  Division

See also

• Fixed Point
• Floating Point
• Single Precision
• Double Precision

References

• Survey of Floating-Point Formats

External links

• OpenGL half float pixel