Reuleaux triangle

The Reuleaux triangle is a constant width curve based on an equilateral triangle. The distances from any point on a side to the opposite vertex are all equal.

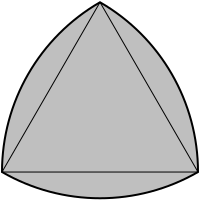
A Reuleaux polygon is a curve of constant width - that is, a curve in which all diameters are the same length. The best-known version is the Reuleaux triangle. Both are named after Franz Reuleaux, a 19th-century German engineer who did pioneering work on ways that machines translate one type of motion into another, although it was known before his time.

The Reuleaux triangle rotating inside a constant sized square

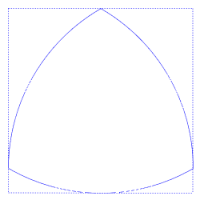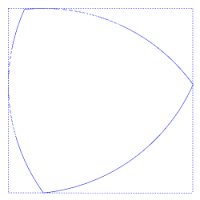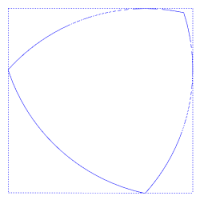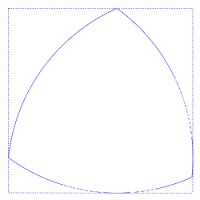
The Reuleaux triangle is the simplest nontrivial example of a curve of constant width - a curve in which the distance between two opposite parallel tangent lines to its boundary is the same, regardless of the direction of those two parallel lines. (The trivial example would be a circle.)

To construct the Reuleaux triangle, start with an equilateral triangle. Center a compass at one vertex and sweep out the (minor) arc between the other two vertices. Do the same with the compass centered at each of the other vertices. Delete the original triangle. The result is a curve of constant width. Equivalently, given an equilateral triangle T of side length s, take the boundary of the intersection of the disks with radius s centered at the vertices of T.

By the Blaschke-Lebesgue theorem, the Reuleaux triangle has the least area of any curve of given constant width. This area is ${1 \over 2}(\pi -{\sqrt {3}})s^{2}$, where s is the constant width.

The Reuleaux triangle can be generalized to regular polygons with an odd number of sides. See also the British Twenty Pence and Fifty Pence coins.

Other uses

• Because all of its diameters are the same length, the Reuleaux triangle, along with all other Reuleaux polygons, is an answer to the question "Other than a circle, what shape can you make a manhole cover so that it cannot fall down through the hole?"

• The rotor of the Wankel engine is similar to a Reuleaux triangle.

• A drill bit in the shape of a Reuleaux triangle can (if mounted in an apparatus that doesn't rotate it along its axis) drill a hole that is very nearly a perfect square.

• A Reuleaux triangle rolls smoothly and easily, but does not make a good wheel because it does not have a fixed center of rotation. While an object on top of rollers with cross-sections that were Reuleaux triangles would roll smoothly and flatly, an axle attached to wheels shaped like Reuleaux triangles would bounce up and down three times per revolution. This concept was used in a science fiction short story by Poul Anderson titled "The Three-Cornered Wheel."

• The existence of Reuleaux polygons is a good demonstration of why you cannot use diameter measurements alone to verify that an object has a circular cross-section.

• Several pencils are manufactured in this shape, rather than the more traditional round or hexagonal barrels. They are usually promoted as being more comfortable or encouraging proper grip (if marketed for children), as well as having the advantage of not rolling off tables.

Three-dimensional version

The intersection of the balls of radius s centered at the vertices of a regular tetrahedron with side length s is called the Reuleaux tetrahedron, but is not a surface of constant width. It can, however, be made into a surface of constant width, called Meissner's tetrahedron, by replacing its edge arcs by curved surface patches; alternatively, the surface of revolution of a Reuleaux triangle through one of its symmetry axes forms a surface of constant width, with minimum volume among all surfaces of revolution of given constant width.

External links

• How Round is Your Circle? - book about various geometric properties, including curves and solids of constant width
• Shapes of constant width at cut-the-knot
• Russian-language site with downloadable films about the Reuleaux triangle, also showing the Wankel engine and the mechanics of a famous Soviet film projector