KenKen: Difference between revisions
m Date maintenance tags and general fixes |
|||
| Line 43: | Line 43: | ||
== External links == |
== External links == |
||
*[http://www.time.com/time/arts/article/0,8599,1882455,00.html Puzzle Guru Will Shortz], [[Time (magazine)|''Time Magazine'']], March 2, 2009 |
*[http://www.time.com/time/arts/article/0,8599,1882455,00.html Puzzle Guru Will Shortz], [[Time (magazine)|''Time Magazine'']], March 2, 2009 |
||
*[http://www.quazen.com/Games/Puzzles/Kenken-V-Sudoku.107490 A comparison on KenKen and Sudoku] |
|||
[[Category:Mathematics and culture]] |
[[Category:Mathematics and culture]] |
||
Revision as of 16:46, 8 April 2009
This article includes a list of references, related reading, or external links, but its sources remain unclear because it lacks inline citations. (March 2009) |
KenKen or KEN-KEN is a style of arithmetic and logical puzzle sharing several characteristics with sudoku. The name comes from Japanese and translates as "the square of wisdom" or "cleverness squared".[1]
KenKen was invented in 2004 by the Japanese math teacher Tetsuya Miyamoto, an innovator who says he practices "the art of teaching without teaching".[1] He intends the puzzles as an instruction-free method of training the brain.[2] The toy inventor Robert Fuhrer encountered books of them published in Japan by the educational publisher Gakken Co., Ltd. and titled "Kashikoku naru Puzzle".[citation needed] Fuhrer's company Nextoy, LLC (now holder of a trademark on "KenKen" as a name for brain-training puzzles) and chess International Master Dr. David Levy helped bring the puzzles to the attention of Michael Harvey, features editor of The Times' of London.[citation needed] Harvey, impressed what he calls its "depth and magnitude", arranged for publication of such puzzles, starting in March 2008, in The Times.[This quote needs a citation] Other papers, including the New York Times, followed suit.
Each puzzle is presented on a square grid of size 3 to 9. The number of cells on each horizontal or vertical side of the grid matches that size, and the puzzle is to be solved by placing in each cell a number, from 1 to the puzzle size inclusive, that is consistent with the clues provided.
The grid is divided into several "cages" reminiscent of the non-square-region Sudoku variants, but permitting variable numbers of cells in the cages of the same puzzle. Each cage is a polyomino: each cell of the cage connects indirectly with all the rest via pairs of adjacent vertical sides and of adjacent horizontal sides.
Each clue constrains the collection of numbers that may appear in the cage's cells; only cage contents that collectively satisfy the clue can be part of a solution of the puzzle. The style of typical clues in KenKen is a combination of an arithmetical operation (addition, subtraction, multiplication, or division) and a numerical result. (However, no operation is relevant for a single-cell cage: placing the "result" in the cell is the only possibility considered to satisfy the clue.) A three-cell cage specifying addition and a result of 6 in a size-of-4 puzzle might be satisfied with the digits 1, 2, and 3. In contrast to Suduko, however, KenKen forbids repetition only among the numbers in a row or the numbers in a column, and does not automatically rule out repetition within a cage. For example, if the three-cell region adding to 6 has two cells adjacent horizontally but the third adjacent vertically to one of them, 4 in the center "cell", and 1 in the two "end" cells would also satisfy the clue.
In the English-language KenKen books of Will Shortz, the issue of the non-associativity of division and subtraction is addressed by restricting clues based on either of those operations to cages of only two cells.
Example
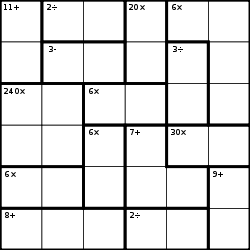

The objective is to fill the grid in with the digits 1 through 6 such that:
- Each row contains exactly one of each digit
- Each column contains exactly one of each digit
- Each bold-outlined group of cells is a cage containing digits which achieve the specified result using the specified mathematical operation: addition (+), subtraction (-), multiplication (×), and division (÷). (Unlike in Killer Sudoku, digits may repeat within a group.)
Some of the techniques from Sudoku and Killer Sudoku can be used here, but much of the process involves the listing of all the possible options and eliminating the options one by one as other information requires.
In the example here:
- "11+" in the leftmost column can only be "5,6"
- "2÷" in the top row must be one of "1,2", "2,4" or "3,6"
- "20x" in the top row must be "4,5".
- "6x" in the top right must be "1,1,2,3". Therefore the two "1"s must be in separate columns, thus row 1 column 5 is a "1".
- "240x" on the left side is one of "6,5,4,2" or "3,5,4,4". Either way there is a five and it must be in the right pair of cells since we have "5,6" already in column 1.
- etc.
Extensions
More complex KenKen problems are formed using the principles described above but omitting the symbols +, -, x and ÷, thus leaving them as yet another unknown to be determined.
The restriction of puzzle size to the range two through nine is not absolute. A KenKen of size two is of little value even as an example, as it can immediately be solved by trying the two possibilities — ones on the "rising" diagonal and twos on the "falling" one, or vice versa. But extension beyond nine presents only difficulties of calculation with larger numbers, and the need, in recording possible values, to avoid confusing multi-digit numbers with items in a list of single digit ones.
References
- ^ a b A New Puzzle Challenges Math Skills, New York Times, February 8, 2009
- ^ Tetsuya Miyamoto creates KenKen. Train your brain, The Times, 21 March 2008
External links
- Puzzle Guru Will Shortz, Time Magazine, March 2, 2009
- A comparison on KenKen and Sudoku
