Equidistant: Difference between revisions
m Bot: Migrating 1 interwiki links, now provided by Wikidata on d:q4386982 |
Correction of mathematical mistake and correction of terminology. |
||
| Line 5: | Line 5: | ||
[[File:Perpendicular bisector.gif|right|thumb|Bisection of two [[circular segment]]s by a line. All the points on the red line are equidistant from the two end points of the black line.]] |
[[File:Perpendicular bisector.gif|right|thumb|Bisection of two [[circular segment]]s by a line. All the points on the red line are equidistant from the two end points of the black line.]] |
||
[[File:Skel.png|thumb|right|A shape and its skeleton, computed with a [[topology]]-preserving [[thinning algorithm]].]] |
[[File:Skel.png|thumb|right|A shape and its skeleton, computed with a [[topology]]-preserving [[thinning algorithm]].]] |
||
[[File:Circumscribed Polygon.svg|thumb|The |
[[File:Circumscribed Polygon.svg|thumb|The [[cyclic polygon]] P is [[circumscribed circle|circumscribed]] by the circle C. The circumcentre O is equidistant to each point on the circle, and a fortiori to each vertex of the polygon.]] |
||
A point is said to be '''equidistant''' from a set of objects if the [[distance]]s between that point and each object in the set are equal.<ref>{{cite book |
A point is said to be '''equidistant''' from a set of objects if the [[distance]]s between that point and each object in the set are equal.<ref>{{cite book |
||
Revision as of 20:15, 5 April 2013
 | This article needs additional citations for verification. (August 2012) |
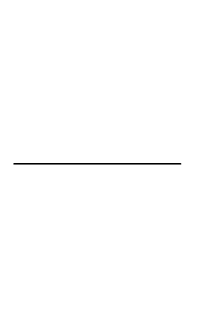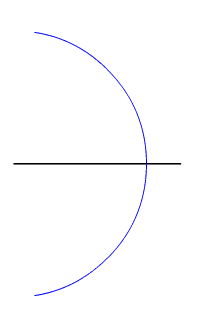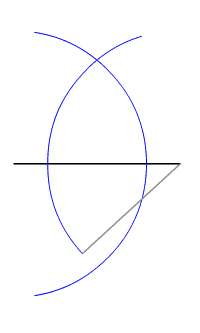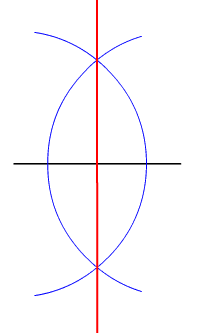
A point is said to be equidistant from a set of objects if the distances between that point and each object in the set are equal.[1]
In two-dimensional Euclidian geometry the locus of points equidistant from two given (different) points is their perpendicular bisector. In three dimensions, the locus of points equidistant from two given points is a plane, and generalising further, in n-dimensional space the locus of points equidistant from two points in n-space is an (n−1)-space.
For a triangle the circumcentre is a point equidistant from each of the three end points. Every non degenerate triangle has such a point. This result can be generalised to cyclic polygons. The center of a circle is equidistant from every point on the circle. Likewise the center of a sphere is equidistant from every point on the sphere.
A parabola is the set of points in a plane equidistant from a fixed point (the focus) and a fixed line (the directrix), where distance from the directrix is measured along a line perpendicular to the directrix.
In shape analysis, the topological skeleton or medial axis of a shape is a thin version of that shape that is equidistant from its boundaries.
References
- ^ Clapham, Christopher; Nicholson, James (2009). The concise Oxford dictionary of mathematics. Oxford University Press. pp. 164–165. ISBN 978-0-19-923594-0.
 | This elementary geometry-related article is a stub. You can help Wikipedia by expanding it. |