Congruence (geometry)

An example of congruence. The two figures on the left are congruent, while the third is similar to them. The last figure is neither. Note that congruences alter some properties, such as location and orientation, but leave others unchanged, like distances and angles. The latter sort of properties are called invariants and studying them is the essence of geometry.

In geometry, two sets are called congruent if one can be transformed into the other by an isometry, i.e., a combination of translations, rotations and reflections. In less formal language, two sets are congruent if they have the same shape and size, but are in different positions (for instance one may be rotated, flipped, or simply moved).

Note: This article is about congruences in geometry. For notions of congruence in algebra, see congruence relation.

Definition of congruence in analytic geometry

In a Euclidean system, congruence is fundamental; it's the counterpart of an equals sign in numerical analysis. In analytic geometry, congruence may be defined intuitively thus: two mappings of figures onto one Cartesian coordinate system are congruent if and only if, for any two points in the first mapping, the Euclidean distance between them is equal to the Euclidean distance between the corresponding points in the second mapping.

A more formal definition: two subsets A and B of Euclidean space Rⁿ are called congruent if there exists an isometry f : Rⁿ → Rⁿ (an element of the Euclidean group E(n)) with f(A) = B. Congruence is an equivalence relation.

Congruence of triangles

Two triangles are congruent if their corresponding sides and angles are equal. Usually it is sufficient to establish the equality of three corresponding parts and use one of the following results to conclude the congruence of the two triangles.

The shape of a triangle is determined up to congruence by specifying two sides and the angle between them (SAS), two angles and the side between them (ASA) or two angles and an adjacent side (AAS). Specifying two sides and an adjacent angle (SSA), however, usually yields two distinct possible triangles.

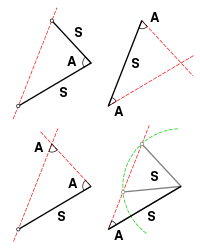
SAS, SSS, and ASA

SAS (Side-Angle-Side): Two triangles are congruent if a pair of corresponding sides and the included angle are congruent.

SSS (Side-Side-Side): Two triangles are congruent if their corresponding sides are congruent.

ASA (Angle-Side-Angle): Two triangles are congruent if a pair of corresponding angles and the included side are congruent. The ASA Postulate was contributed by Thales of Miletus (Greek).

In most system of axioms, the three criteria — SAS, SSS and ASA — are established as theorems. However, in the infamous SMSG system which heralded the short lived infatuation with the New Math stream in mathematics education, SAS is taken as one (#15) of 22 postulates.

SSA: The ambiguous case

While the AAS (Angle-Angle-Side) condition also guarantees congruence, SSA (Side-Side-Angle) does not, as there are often two dissimilar triangles with a pair of corresponding sides and a non-included angle equal. This is known as the ambiguous case.

It is often said that to remember that the "SSA" does not work, all you have to do is spell it backward.

However, a special case of the SSA condition is the HL (Hypotenuse-Leg) condition, also called the RHS (Right Angle-Hypotenuse-Side). This is true because all right triangles (which this condition is used with) have a congruent angle (the right angle). If the hypotenuse and a certain leg of a triangle are congruent to the corresponding hypotenuse and leg of a different triangle, the two triangles are congruent.

SSA is also valid if, of the angle and sides which are known to be equal, the side opposite the angle is longer than the other side.

AAA

AAA (Angle-Angle-Angle) says nothing about the size of the two triangles and hence shows only similarity and not congruence.

See also

• Euclidean plane isometry
• CPCTC

External links

• The SSS
• The SSA
• Congruent angles With interactive animation
• Congruent line segments With interactive animation