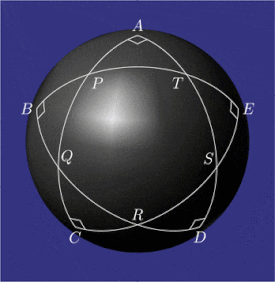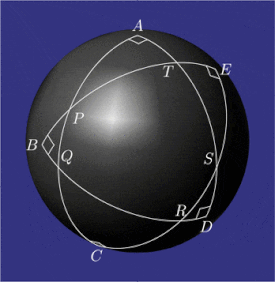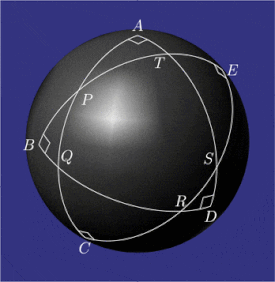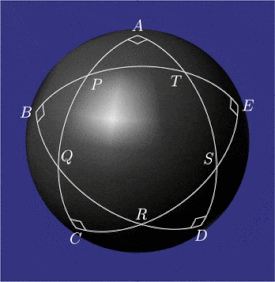
Sample configurations of pentagramma mirificum Relations between the angles and sides of five right triangles adjacent to the inner pentagon. Their Napier’s circles contain circular shifts of parts
(
a
,
{\displaystyle (a,}
π
/
2
−
B
,
{\displaystyle \pi /2-B,}
π
/
2
−
c
,
{\displaystyle \pi /2-c,}
π
/
2
−
A
,
{\displaystyle \pi /2-A,}
b
)
{\displaystyle b)}
Pentagramma mirificum Latin for "miraculous pentagram") is a star polygon on a sphere , composed of five great circle arcs , all of whose internal angles are right angles . This shape was described by John Napier in his 1614 book Mirifici Logarithmorum Canonis Descriptio Description of the Admirable Table of Logarithms ) along with rules that link the values of trigonometric functions of five parts of a right spherical triangle (two angles and three sides). The properties of pentagramma mirificum were studied, among others, by Carl Friedrich Gauss .[ 1]
Geometric properties [ edit ] On a sphere, both the angles and the sides of a triangle (arcs of great circles) are measured as angles.
There are five right angles, each measuring
π
/
2
,
{\displaystyle \pi /2,}
A
{\displaystyle A}
B
{\displaystyle B}
C
{\displaystyle C}
D
{\displaystyle D}
E
.
{\displaystyle E.}
There are ten arcs, each measuring
π
/
2
:
{\displaystyle \pi /2:}
P
C
{\displaystyle PC}
P
E
{\displaystyle PE}
Q
D
{\displaystyle QD}
Q
A
{\displaystyle QA}
R
E
{\displaystyle RE}
R
B
{\displaystyle RB}
S
A
{\displaystyle SA}
S
C
{\displaystyle SC}
T
B
{\displaystyle TB}
T
D
.
{\displaystyle TD.}
In the spherical pentagon
P
Q
R
S
T
{\displaystyle PQRST}
P
{\displaystyle P}
R
S
{\displaystyle RS}
Q
{\displaystyle Q}
S
T
{\displaystyle ST}
At each vertex of pentagon
P
Q
R
S
T
{\displaystyle PQRST}
external angle is equal in measure to the opposite side. For instance,
∠
A
P
T
=
∠
B
P
Q
=
R
S
,
∠
B
Q
P
=
∠
C
Q
R
=
S
T
,
{\displaystyle \angle APT=\angle BPQ=RS,\;\angle BQP=\angle CQR=ST,}
Napier's circles of spherical triangles
A
P
T
{\displaystyle APT}
B
Q
P
{\displaystyle BQP}
C
R
Q
{\displaystyle CRQ}
D
S
R
{\displaystyle DSR}
E
T
S
{\displaystyle ETS}
rotations of one another.
Gauss introduced the notation
(
α
,
β
,
γ
,
δ
,
ε
)
=
(
tan
2
T
P
,
tan
2
P
Q
,
tan
2
Q
R
,
tan
2
R
S
,
tan
2
S
T
)
.
{\displaystyle (\alpha ,\beta ,\gamma ,\delta ,\varepsilon )=(\tan ^{2}TP,\tan ^{2}PQ,\tan ^{2}QR,\tan ^{2}RS,\tan ^{2}ST).}
The following identities hold, allowing the determination of any three of the above quantities from the two remaining ones:[ 2]
1
+
α
=
γ
δ
1
+
β
=
δ
ε
1
+
γ
=
α
ε
1
+
δ
=
α
β
1
+
ε
=
β
γ
.
{\displaystyle {\begin{aligned}1+\alpha &=\gamma \delta &1+\beta &=\delta \varepsilon &1+\gamma &=\alpha \varepsilon \\1+\delta &=\alpha \beta &1+\varepsilon &=\beta \gamma .\end{aligned}}}
Gauss proved the following "beautiful equality" (schöne Gleichung ):[ 2]
α
β
γ
δ
ε
=
3
+
α
+
β
+
γ
+
δ
+
ε
=
(
1
+
α
)
(
1
+
β
)
(
1
+
γ
)
(
1
+
δ
)
(
1
+
ε
)
.
{\displaystyle {\begin{aligned}\alpha \beta \gamma \delta \varepsilon &=\;3+\alpha +\beta +\gamma +\delta +\varepsilon \\&=\;{\sqrt {(1+\alpha )(1+\beta )(1+\gamma )(1+\delta )(1+\varepsilon )}}.\end{aligned}}}
It is satisfied, for instance, by numbers
(
α
,
β
,
γ
,
δ
,
ε
)
=
(
9
,
2
/
3
,
2
,
5
,
1
/
3
)
{\displaystyle (\alpha ,\beta ,\gamma ,\delta ,\varepsilon )=(9,2/3,2,5,1/3)}
α
β
γ
δ
ε
{\displaystyle \alpha \beta \gamma \delta \varepsilon }
20
{\displaystyle 20}
Proof of the first part of the equality:
α
β
γ
δ
ε
=
α
β
γ
(
1
+
α
γ
)
(
1
+
γ
α
)
=
β
(
1
+
α
)
(
1
+
γ
)
=
β
+
α
β
+
β
γ
+
α
β
γ
=
β
+
(
1
+
δ
)
+
(
1
+
ε
)
+
α
(
1
+
ε
)
=
2
+
α
+
β
+
δ
+
ε
+
1
+
γ
=
3
+
α
+
β
+
γ
+
δ
+
ε
{\displaystyle {\begin{aligned}\alpha \beta \gamma \delta \varepsilon &=\alpha \beta \gamma \left({\frac {1+\alpha }{\gamma }}\right)\left({\frac {1+\gamma }{\alpha }}\right)=\beta (1+\alpha )(1+\gamma )\\&=\beta +\alpha \beta +\beta \gamma +\alpha \beta \gamma =\beta +(1+\delta )+(1+\varepsilon )+\alpha (1+\varepsilon )\\&=2+\alpha +\beta +\delta +\varepsilon +1+\gamma \\&=3+\alpha +\beta +\gamma +\delta +\varepsilon \end{aligned}}}
Proof of the second part of the equality:
α
β
γ
δ
ε
=
α
2
β
2
γ
2
δ
2
ε
2
=
γ
δ
⋅
δ
ε
⋅
ε
α
⋅
α
β
⋅
β
γ
=
(
1
+
α
)
(
1
+
β
)
(
1
+
γ
)
(
1
+
δ
)
(
1
+
ε
)
{\displaystyle {\begin{aligned}\alpha \beta \gamma \delta \varepsilon &={\sqrt {\alpha ^{2}\beta ^{2}\gamma ^{2}\delta ^{2}\varepsilon ^{2}}}\\&={\sqrt {\gamma \delta \cdot \delta \varepsilon \cdot \varepsilon \alpha \cdot \alpha \beta \cdot \beta \gamma }}\\&={\sqrt {(1+\alpha )(1+\beta )(1+\gamma )(1+\delta )(1+\varepsilon )}}\end{aligned}}}
From Gauss comes also the formula[ 2]
(
1
+
i
α
)
(
1
+
i
β
)
(
1
+
i
γ
)
(
1
+
i
δ
)
(
1
+
i
ε
)
=
α
β
γ
δ
ε
e
i
A
P
Q
R
S
T
,
{\displaystyle (1+i{\sqrt {^{^{\!}}\alpha }})(1+i{\sqrt {\beta }})(1+i{\sqrt {^{^{\!}}\gamma }})(1+i{\sqrt {\delta }})(1+i{\sqrt {^{^{\!}}\varepsilon }})=\alpha \beta \gamma \delta \varepsilon e^{iA_{PQRST}},}
A
P
Q
R
S
T
=
2
π
−
(
|
P
Q
⌢
|
+
|
Q
R
⌢
|
+
|
R
S
⌢
|
+
|
S
T
⌢
|
+
|
T
P
⌢
|
)
{\displaystyle A_{PQRST}=2\pi -(|{\overset {\frown }{PQ}}|+|{\overset {\frown }{QR}}|+|{\overset {\frown }{RS}}|+|{\overset {\frown }{ST}}|+|{\overset {\frown }{TP}}|)}
P
Q
R
S
T
{\displaystyle PQRST}
Gnomonic projection [ edit ] The image of spherical pentagon
P
Q
R
S
T
{\displaystyle PQRST}
gnomonic projection (a projection from the centre of the sphere) onto any plane tangent to the sphere is a rectilinear pentagon. Its five vertices
P
′
Q
′
R
′
S
′
T
′
{\displaystyle P'Q'R'S'T'}
unambiguously determine a conic section ; in this case — an ellipse . Gauss showed that the altitudes of pentagram
P
′
Q
′
R
′
S
′
T
′
{\displaystyle P'Q'R'S'T'}
O
′
{\displaystyle O'}
Arthur Cayley observed that, if we set the origin of a Cartesian coordinate system in point
O
′
{\displaystyle O'}
P
′
Q
′
R
′
S
′
T
′
{\displaystyle P'Q'R'S'T'}
(
x
1
,
y
1
)
,
…
,
{\displaystyle (x_{1},y_{1}),\ldots ,}
(
x
5
,
y
5
)
{\displaystyle (x_{5},y_{5})}
x
1
x
4
+
y
1
y
4
=
{\displaystyle x_{1}x_{4}+y_{1}y_{4}=}
x
2
x
5
+
y
2
y
5
=
{\displaystyle x_{2}x_{5}+y_{2}y_{5}=}
x
3
x
1
+
y
3
y
1
=
{\displaystyle x_{3}x_{1}+y_{3}y_{1}=}
x
4
x
2
+
y
4
y
2
=
{\displaystyle x_{4}x_{2}+y_{4}y_{2}=}
x
5
x
3
+
y
5
y
3
=
−
ρ
2
{\displaystyle x_{5}x_{3}+y_{5}y_{3}=-\rho ^{2}}
ρ
{\displaystyle \rho }
[ 3]

 Media related to Pentagramma mirificum at Wikimedia Commons
Media related to Pentagramma mirificum at Wikimedia Commons




















































