Gridiron pendulum

Zinc-steel gridiron with 5 rods

Brass-steel gridiron with 9 rods

Tubular version, with zinc and steel concentric tubes

Ellicott pendulum, another version

The gridiron pendulum was a temperature-compensated clock pendulum invented by British clockmaker John Harrison around 1726.^[1]^[2]^[3]^[4] It was used in precision clocks. In ordinary clock pendulums, the pendulum rod expands and contracts with changes in temperature. The period of the pendulum's swing depends on its length, so a pendulum clock's rate varied with changes in ambient temperature, causing inaccurate timekeeping. The gridiron pendulum consists of alternating parallel rods of two metals with different thermal expansion coefficients, such as steel and brass. The rods are connected by a frame in such a way that their different thermal expansions (or contractions) compensate for each other, so that the overall length of the pendulum, and thus its period, stays constant with temperature.

The gridiron pendulum was used during the Industrial Revolution period in pendulum clocks, particularly precision regulator clocks^[1] employed as time standards in factories, laboratories, office buildings, railroad stations and post offices to schedule work and set other clocks. The gridiron became so associated with accurate timekeeping that by the turn of the 20th century many clocks had pendulums with decorative fake gridirons, which had no temperature compensating qualities.^[1]^[4]

How it works

A: exterior schematic
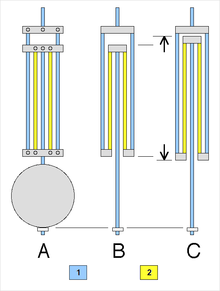
B: normal temperature
C: higher temperature

The gridiron pendulum is constructed so the high thermal expansion (zinc or brass) rods make the pendulum shorter when they expand, while the low expansion steel rods make the pendulum longer. By using the correct ratio of lengths, the greater expansion of the zinc or brass rods exactly compensate for the greater length of the low expansion steel rods, and the pendulum stays the same length with temperature changes.^[2]

The simplest form of gridiron pendulum, introduced as an improvement to Harrison's around 1750 by John Smeaton, consists of five rods, 3 of steel and two of zinc. A central steel rod runs up from the bob to a point immediately below the suspension.

At that point a cross-piece (middle bridge) extends from the central rod and connects to two zinc rods, one on each side of the central rod, which reach down to, and are fixed to, the bottom bridge just above the bob. The bottom bridge clears the central rod and connects to two further steel rods which run back up to the top bridge attached to the suspension. As the steel rods expand in heat, the bottom bridge drops relative to the suspension, and the bob drops relative to the middle bridge. However, the middle bridge rises relative to the bottom one because the greater expansion of the zinc rods pushes the middle bridge, and therefore the bob, upward to match the combined drop caused by the expanding steel.

In simple terms, the upward expansion of the zinc counteracts the combined downward expansion of the steel (which has a greater total length). The rod lengths are calculated so that the effective length of the zinc rods multiplied by zinc's thermal expansion coefficient equals the effective length of the steel rods multiplied by iron's expansion coefficient, thereby keeping the pendulum the same length.

Harrison's original pendulum used brass rods (pure zinc not being available then); these required more rods because brass does not expand as much as zinc does. Instead of one high expansion rod on each side, two are needed on each side, requiring a total of 9 rods, five steel and four brass.^[3]^[4] The exact degree of compensation can be adjusted by having a section of the central rod which is partly brass and partly steel. These overlap (like a sandwich) and are joined by a pin which passes through both metals. A number of holes for the pin are made in both parts and moving the pin up or down the rod changes how much of the combined rod is brass and how much is steel.

In the late 19th century the Dent company developed a tubular version of the zinc gridiron in which the four outer rods were replaced by two concentric tubes which were linked by a tubular nut which could be screwed up and down to alter the degree of compensation.

In the 1730s clockmaker John Ellicott designed a version that only required 3 rods, two brass and one steel (see drawing), in which the brass rods as they expanded with increasing temperature pressed against levers which lifted the bob.^[5]^[1] The Ellicott pendulum did not see much use.^[6]^{: p.272-273}

Disadvantages

Scientists in the 1800s found that the gridiron pendulum had disadvantages that made it unsuitable for the highest-precision clocks.^[4] The friction of the rods sliding in the holes in the frame caused the rods to adjust to temperature changes in a series of tiny jumps, rather than with a smooth motion. This caused the rate of the pendulum, and therefore the clock, to change suddenly with each jump. Later it was found that zinc is not very stable dimensionally; it is subject to creep. Therefore, another type of temperature-compensated pendulum, the mercury pendulum invented in 1721 by George Graham, was used in the highest-precision clocks.^[4]

By 1900, the highest-precision astronomical regulator clocks used pendulum rods of low thermal expansion materials such as invar^[3]^[2] and fused quartz.

Gallery

Analysis

All substances expand with an increase in temperature $\theta$ , so uncompensated pendulum rods get longer with a temperature increase, causing the clock to slow down, and shrink with a temperature decrease, causing the clock to speed up. The amount depends on the linear coefficient of thermal expansion (CTE) $\alpha$ of the material they are composed of. CTE is usually given in parts per million per degree Celsius. The expansion or contraction of a rod of length $L$ with a coefficient of expansion $\alpha$ caused by a temperature change $\Delta \theta$ is^[7]^{: p.250, eq.10.19}

\Delta L=\alpha L\Delta \theta

(1)

Temperature error

The period of oscillation $T$ of the pendulum (the time interval for a right swing and a left swing) is^[7]^{: p.239, eq.10.2}

T=2\pi {\sqrt {L \over g}}

(2)

A change in length $\Delta L$ due to a temperature change $\Delta \theta$ will cause a change in the period $\Delta T$ . Since the expansion coefficient is so small, the length changes due to temperature are very small, parts per million, so $\Delta T<<T$ and the change in period can be approximated to first order as a linear function^[7]^: p.250

\Delta T={\partial T \over \partial L}\Delta L

\qquad ={\partial  \over \partial L}{\Big (}2\pi {\sqrt {L \over g}}{\Big )}\Delta L=\pi {\Delta L \over {\sqrt {gL}}}

Substituting equation (1), the change in the pendulum's period caused by a change in temperature $\Delta \theta$ is

\qquad =\pi {\alpha L\Delta \theta  \over {\sqrt {gL}}}=\alpha \pi {\sqrt {L \over g}}\Delta \theta

\Delta T={\alpha T\Delta \theta  \over 2}

$\quad {\Delta T \over T}={\alpha \Delta \theta \over 2}\quad$

So the fractional change in an uncompensated pendulum's period is equal to one-half the coefficient of expansion times the change in temperature.

Steel has a CTE of 11.5 x 10⁻⁶ per °C so a pendulum with a steel rod will have a thermal error rate of 5.7 parts per million or 0.5 seconds per day per degree Celsius (0.9 seconds per day per degree Fahrenheit). Before 1900 most buildings were unheated, so clocks in temperate climates like Europe and North America would experience a summer/winter temperature variation of around 14 °C (25 °F) resulting in an error rate of 6.8 seconds per day.^[6]^: p.259 Wood has a smaller CTE of 4.9 x 10⁻⁶ per °C thus a pendulum with a wood rod will have a smaller thermal error of 0.21 sec per day per °C, so wood pendulum rods were often used in quality domestic clocks. The wood had to be varnished to protect it from the atmosphere as humidity could also cause changes in length.

Compensation

A gridiron pendulum is symmetrical, with two identical chains of suspension rods, one on each side, suspending the bob from the pivot. Within each suspension chain, the total change in length of the pendulum is equal to the sum of the changes of the rods that make it up.

It is designed so the high expansion rods on each side push the pendulum bob up, in the opposite direction to the low expansion rods, so the net change in length is the difference between these changes. From (1) the change in length $\Delta L$ of a gridiron pendulum with a temperature change $\Delta \theta$ is

\Delta L=\sum \Delta L_{\text{low}}-\sum \Delta L_{\text{high}}

\Delta L=(\alpha _{\text{low}}\sum L_{\text{low}}-\alpha _{\text{high}}\sum L_{\text{high}})\Delta \theta

where $\sum L_{\text{low}}$ is the sum of the lengths of all the low expansion (steel) rods and $\sum L_{\text{high}}$ is the sum of the lengths of the high expansion rods in the suspension chain from the bob to the pivot. The condition for zero length change with temperature is

\alpha _{\text{low}}\sum L_{\text{low}}-\alpha _{\text{high}}\sum L_{\text{high}}=0

{\alpha _{\text{high}} \over \alpha _{\text{low}}}={\sum L_{\text{low}} \over \sum L_{\text{high}}}

(3)

In other words, the ratio of thermal expansion coefficients of the two metals must be equal to the inverse ratio of the total rod lengths.^[8]^: p.289

Five rod gridiron

In the 5 rod gridiron, there is one high expansion rod on each side, of length $L_{\text{2}}$ , flanked by two low expansion rods with lengths $L_{\text{1}}$ and $L_{\text{3}}$ , one from the pivot to support the bottom of $L_{\text{2}}$ , the other goes from the top of $L_{\text{2}}$ down to support the bob. So from equation (3) the condition for compensation is

{\alpha _{\text{high}} \over \alpha _{\text{low}}}={L_{\text{1}}+L_{\text{3}} \over L_{\text{2}}}

Since to fit in the frame the high expansion rod must be equal to or shorter than each of the low expansion rods $L_{\text{1}}\geq L_{\text{2}}$ and $L_{\text{3}}\geq L_{\text{2}}$ the geometrical condition for construction of the gridiron is

L_{\text{1}}+L_{\text{3}}\geq 2L_{\text{2}}

Therefore the 5 rod gridiron can only be made with metals whose expansion coefficients have a ratio greater than or equal to two^[7]^: p.251

{\alpha _{\text{high}} \over \alpha _{\text{low}}}={L_{\text{1}}+L_{\text{3}} \over L_{\text{2}}}\geq 2

Zinc has a CTE of $\alpha$ = 26.2 x 10⁻⁶ per °C, a ratio of $\alpha _{\text{high}}/\alpha _{\text{low}}$ = 2.28 times steel, so the zinc/steel combination can be used in 5 rod pendulums.
The compensation condition for a zinc/steel gridiron is

{\alpha _{\text{high}} \over \alpha _{\text{low}}}={L_{\text{1}}+L_{\text{3}} \over L_{\text{2}}}=2.28

In addition the total length of the pendulum must give the required period $L_{\text{1}}+L_{\text{3}}-L_{\text{2}}=g{\big (}{\theta \over 2\pi }{\big )}$ . Most of the precision pendulum clocks with gridirons used a 'seconds pendulum', in which the period was two seconds. The length of the seconds pendulum was 0.993 meter so

L_{\text{1}}+L_{\text{3}}-L_{\text{2}}=0.993

Nine rod gridiron

To allow the use of metals with a lower ratio of expansion coefficients, such as brass and steel, a construction with more high expansion rods must be used. In the 9 rod gridiron, there are two high expansion rods on each side, of length $L_{\text{2}}$ and $L_{\text{4}}$ , flanked by three low expansion rods with lengths $L_{\text{1}}$ , $L_{\text{3}}$ and $L_{\text{5}}$ . So from equation (3) the condition for compensation is

{\alpha _{\text{high}} \over \alpha _{\text{low}}}={L_{\text{1}}+L_{\text{3}}+L_{\text{5}} \over L_{\text{2}}+L_{\text{4}}}

Since to fit in the frame each of the two high expansion rods must be as short as or shorter than each of the high expansion rods, the geometrical condition for construction is

L_{\text{1}}+L_{\text{3}}+L_{\text{5}}\geq {3 \over 2}(L_{\text{2}}+L_{\text{2}})

Therefore the 9 rod gridiron can be made with metals with a ratio of thermal expansion coefficients exceeding 1.5^[7]^: p.251

{\alpha _{\text{high}} \over \alpha _{\text{low}}}={L_{\text{1}}+L_{\text{3}}+L_{\text{5}} \over L_{\text{2}}+L_{\text{4}}}\geq 1.5

Brass has a CTE of $\alpha$ = 19.3 x 10⁻⁶ per °C, a ratio of $\alpha _{\text{high}}/\alpha _{\text{low}}$ = 1.68 times steel. So while brass/steel cannot be used in 5 rod gridirons, it can be used in the 9 rod version.

Definition of variables


Symbol	Unit	Definition
$\alpha$	degree Celsius⁻¹	Coefficient of thermal expansion of the pendulum rod
$\alpha _{\text{high}}$	degree Celsius⁻¹	Coefficient of thermal expansion of the high expansion (brass or zinc) rods
$\alpha _{\text{low}}$	degree Celsius⁻¹	Coefficient of thermal expansion of the low expansion (steel) rods
$\theta$	degree Celsius	Ambient temperature
$\pi$	none	Mathematical constant (3.14159...)
$g$	meter×second⁻²	Acceleration of gravity
$L$	meter	Length of pendulum rod from the pivot to center of gravity of the bob
$\sum L_{\text{high}}$	meter	Sum of the lengths of the high expansion gridiron rods
$\sum L_{\text{low}}$	meter	Sum of the lengths of the low expansion gridiron rods
$L_{\text{n}}$	meter	Length of the n-th gridiron rod
$T$	second	Period of the pendulum (time for a complete cycle of two swings)

References

^ ^a ^b ^c ^d Turner, Anthony; Nye, James; Betts, Jonathan (2022). A General History of Horology. Oxford University Press. p. 321. ISBN 9780192609366.
^ ^a ^b ^c Baker, Gregory L. (2011). Seven Tales of the Pendulum. Oxford University Press. pp. 79–82. ISBN 9780191004841.
^ ^a ^b ^c "Clock". Encyclopaedia Britannica, 11th Ed. Vol. 6. The Encyclopaedia Brittanica Co. 1910. p. 539. Retrieved 7 July 2024.
^ ^a ^b ^c ^d ^e Matthys, Robert J. (2004). Accurate Clock Pendulums. Oxford University Press. pp. 8–10. ISBN 9780198529712.
^ Beckett, Edmund (Lord Grimsthorpe) (1874). A Rudimentary Treatise on Clocks and Watches and Bells, 6th Ed. London: Lockwood & Co. p. 59-60.
^ ^a ^b Kater, Henry; Lardner, Dionysus (1831). A Treatise on Mechanics. Philadelphia: Carey and Lea.
^ ^a ^b ^c ^d ^e Baker, Gregory L.; Blackburn, James A. (2005). The Pendulum: A Case Study in Physics. Oxford University Press. ISBN 9780198567547.
^ Glasgow, David (1885). Watch and Clock Making. London: Cassell and Co."The total lengths should be inversely proportional to the coefficients of expansion for the metals used"