Jump to content

Tree traversal

From Wikipedia, the free encyclopedia

This is an old revision of this page, as edited by 212.25.124.146 (talk) at 17:35, 30 May 2007. The present address (URL) is a permanent link to this revision, which may differ significantly from the current revision.

In computer science, tree traversal refers to the process of visiting each node in a tree data structure, exactly once, in a systematic way. Such traversals are classified by the order in which the nodes are visited. The following algorithms are described for a binary tree, but they may be generalized to other trees as well.

Traversal methods

Compared to linear data structures like linked lists and one dimensional arrays, which have only one logical means of traversal, tree structures can be traversed in many different ways. Starting at the root of a binary tree, there are three main steps that can be performed and the order in which they are performed define the traversal type. These steps are: Performing an action on the current node (referred to as "visiting" the node); or repeating the process with the subtrees rooted at our left and right children. Thus the process is most easily described through recursion.

To traverse a non-empty binary tree in preorder, we perform the following three operations: 1. Visit the root. 2. Traverse the left subtree in preorder. 3. Traverse the right subtree in preorder.

To traverse a non-empty binary tree in inorder, perform the following operations: 1. Traverse the left subtree in inorder. 2. Visit the root. 3. Traverse the right subtree in inorder.

To traverse a non-empty binary tree in postorder, perform the following operations: 1. Traverse the left subtree in postorder. 2. Traverse the right subtree in postorder. 3. Visit the root. This is also called Depth-first traversal

Finally, trees can also be traversed in level-order, where we visit every node on a level before going to a lower level. This is also called Breadth-first traversal

Sample implementations

preorder(node)
  print node.value
  if node.left  ≠ null then preorder(node.left)
  if node.right ≠ null then preorder(node.right)

inorder(node)
  if node.left  ≠ null then inorder(node.left)
  print node.value
  if node.right ≠ null then inorder(node.right)

postorder(node)
  if node.left  ≠ null then postorder(node.left)
  if node.right ≠ null then postorder(node.right)
  print node.value

All three sample implementations will require stack space proportional to the height of the tree. In a poorly balanced tree, this can be quite considerable.

We can remove the stack requirement by maintaining parent pointers in each node, or by threading the tree. In the case of using threads, this will allow for greatly improved inorder traversal, although retrieving the parent node required for preorder and postorder traversal will be slower than a simple stack based algorithm.

To traverse a threaded tree inorder, we could do something like this: 

inorder(node)
  while hasleftchild(node) do
    node = node.left
  do
    visit(node)
    if not (hasrightchild(node)) then
      node = node.right
      while hasleftchild(node) do
        node = node.left
    else
      node = node.right
  while node ≠ null

Note that a threaded binary tree will provide a means of determining whether a pointer is a child, or a thread. See threaded binary trees for more information.

Level order traversal

The example below is a simple queue based level order traversal, and will require space proportional to the maximum number of nodes at a given depth. This can be as much as the total number of nodes / 2. A more space-efficient approach for this type of traversal can be implemented using an iterative deepening depth-first search. 

levelorder(root) 
  q = empty queue
  q.enqueue(root)
  while not q.empty do
    node := q.dequeue()
    visit(node)
    if node.left ≠ null
      q.enqueue(node.left)
    if node.right ≠ null
      q.enqueue(node.right)

Examples

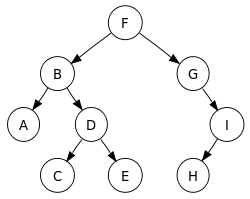
A sorted binary tree In this binary search tree,

V = visit, L = left, R = right

  • Preorder (VLR) traversal yields: F, B, A, D, C, E, G, I, H
  • In-order (LVR) traversal yields: A, B, C, D, E, F, G, H, I
    • Note that the in-order traversal of a binary search tree yields an ordered list
  • Postorder (LRV) traversal yields: A, C, E, D, B, H, I, G, F
  • Level-order traversal yields: F, B, G, A, D, I, C, E, H

Uses

In-order traversal

It is particularly common to traverse a binary search tree in-order, because it gives the values in increasing order.

To see why this is the case, note that if n is a node in a binary search tree, then everything in n 's left subtree is less than n, and everything in n 's right subtree is greater than or equal to n. Thus, if we visit the left subtree in order, using a recursive call, and then visit n, and then visit the right subtree in order, we have visited the entire subtree rooted at n in order. We can assume the recursive calls correctly visit the subtrees in order using the mathematical principle of structural induction. Traversing in reverse in-order similarly gives the values in decreasing order.

Preorder traversal

Traversing a tree in preorder whilst inserting the values in to a new tree, is common way of making a complete copy of a binary search tree.

We can also use preorder traversals to evaluate expression trees.

We scan the expression tree from right to left, placing the elements in a stack.

Each time we find an operator, we replace the two top symbols of the stack by the result of applying the operator to those elements. For instance, the expression ∗ + 234 (which in infix notation is “(2 + 3) ∗ 4”) would be evaluated like this:

Using pre-fix traversal to evaluate an expression tree
Expression (remaining) Stack
∗ + 234 <empty>
∗ + 23 4
∗ + 2 3 4
∗ + 2 3 4
∗ 5 4
Answer 20

Postorder traversal

In comparison to preordered notation that correlates nicely with a stack, postorder notation nicely correlates to a queue.

This prints the nodes in the order of their depth from the root. See the iterative version below.

Functional traversal

We could perform the same traversals in a functional language like Haskell using code similar to this: 

data Tree a = Nil | Node (Tree a) a (Tree a)

preorder Nil = []
preorder (Node left x right) = [x] ++ (preorder left) ++ (preorder right) 

postorder Nil = []
postorder (Node left x right) = (postorder left) ++ (postorder right) ++ [x]

inorder Nil = []
inorder (Node left x right) = (inorder left) ++ [x] ++ (inorder right)

Traversing with parent pointers

All of the above recursive algorithms require stack space proportional to the depth of the tree. If we store on each node a reference to its parent, then we can implement all of these traversals in-place using a simple iterative algorithm. The parent references occupy much more space, however. This is useful if the parent references are needed anyway, stack space in particular is limited or function call overhead (which can be quite significant on some architectures) should be avoided. For example, here is an iterative algorithm for in-order traversal: 

inorder(node)
  if node == null then
    return
  // Start from the minimum node
  while node.left ≠ null do
    node = node.left
  do
    visit(node)
    // Next in order will be our right child's leftmost child (if null, our right child)
    if node.right ≠ null then
      node = node.right
      while node.left ≠ null do
        node = node.left
    else
      // Next in order will be our closest ancestor that hasn't been visited yet
      while true do
        if node.parent == null then
          node = nil
          break
        node = node.parent
        // If node is its parents left child, then its parent hasn't been visited yet
        if node.parent.left == node then
          break
  while node ≠ null

Another advantage of traversing iteratively is that the algorithm can easily be split up to three functions, GetFirstNode(), GetNextNode() and GetPrevNode(). This is not possible using recursive procedures (without using coroutines), and in the example above the only variable needed to keep state is "node".

If we do not have parent pointers, we can provide the same functionality as above by using an explicit stack representation. This is desirable on platforms where recursion is costly, or where we wish to be able to be able to have GetNextNode/GetPrevNode functionality.

The pseudocode (shown below, with key changes underlined) is very similar to with parent pointers, the main change being that we have to remember to push our current node on to a "parent" stack before navigating to a new node. We can then pop nodes back off the parent stack, to get a node's parent and climb back up the tree. 

inorder(node)
  if node == null then
    return
  stack = empty stack
  // Start from the minimum node
  while node.left ≠ null do
    stack.push(node)
    node = node.left
  do
    visit(node)
    // Next in order will be our right child's leftmost child (if null, our right child)
    if node.right ≠ null then
      stack.push(node)
      node = node.right
      while node.left ≠ null do
        stack.push(node)
        node = node.left
    else
      // Next in order will be our closest ancestor that hasn't been visited yet
      while true do
        if stack.empty then
          node = nil
          break
        parent = stack.pop
        // If node is its parents left child, then its parent hasn't been visited yet
        if (parent.left = node) then
          node = parent
          break
        node = parent
  while node ≠ null

A shorter one may look like this: 

 inStackTraverse(node)
   s := new stack
   while (node ≠ nil) or (not s.empty) do
     while node ≠ nil do
       s.push(node)
       node:=node.left
     end do
     node := s.pop()
     visit(node)
     node := node.right
   end do

See also

References

Retrieved from "https://en.wikipedia.org/w/index.php?title=Tree_traversal&oldid=134607386"