Damping (disambiguation)

A damped spring-mass system.

Damping is any effect, either deliberately engendered or inherent to a system, that tends to reduce the amplitude of oscillations of an oscillatory system.

Definition

In physics and engineering, damping may be mathematically modelled as a force synchronous with the velocity of the object but opposite in direction to it. Thus, for a simple mechanical damper, the force F may be related to the velocity v by

${\mathbf {F} }=-c{\mathbf {v} }$

where c is the viscous damping coefficient, given in units of newton-seconds per meter.

This relationship is perfectly analogous to electrical resistance. See Ohm's law.

This force is an (raw) approximation to the friction caused by drag.

In playing stringed instruments such as guitar or violin, damping is the quieting or abrupt silencing of the strings after they have been sounded, by pressing with the edge of the palm, or other parts of the hand such as the fingers on one or more strings near the bridge of the instrument. The strings themselves can be modelled as a continuum of infinitesimally small mass-spring-damper systems where the damping constant is much smaller than the resonance frequency, creating damped oscillations (see below). See also Vibrating string.

Example: mass-spring-damper

A mass attached to a spring and a damper. The damping coefficient, usually c, is represented by B in this case. The F in the diagram denotes an external force, which this example does not include.

An ideal mass-spring-damper system with mass m (in kilograms), spring constant k (in newtons per meter) and viscous damper of damping coeficient c (in newton-seconds per meter) can be described with the following formula:

$F_{\mathrm {s} }=-kx$

$F_{\mathrm {d} }=-cv=-c{\dot {x}}=-c{\frac {dx}{dt}}$

Treating the mass as a free body and applying Newton's second law, we have:

$\sum F=ma=m{\ddot {x}}=m{\frac {d^{2}x}{dt^{2}}}$

where a is the acceleration (in meters per second squared) of the mass and x is the displacement (in meters) of the mass relative to a fixed point of reference.

Differential equation

The above equations combine to form the equation of motion, a second-order differential equation for displacement x as a function of time t (in seconds):

$m{\ddot {x}}+c{\dot {x}}+kx=0.\,$

Rearranging, we have

${\ddot {x}}+{c \over m}{\dot {x}}+{k \over m}x=0.\,$

Next, to simplify the equation, we define the following parameters:

$\omega _{0}={\sqrt {k \over m}}$

and

$\zeta ={c \over 2{\sqrt {km}}}.$

The first parameter, ω₀, is called the (undamped) natural frequency of the system . The second parameter, ζ, is called the damping ratio. The natural frequency represents an angular frequency, expressed in radians per second. The damping ratio is a dimensionless quantity.

The differential equation now becomes

${\ddot {x}}+2\zeta \omega _{0}{\dot {x}}+\omega _{0}^{2}x=0.\,$

Continuing, we can solve the equation by assuming a solution x such that:

$x=e^{\gamma t}\,$

where the parameter $\scriptstyle \gamma$ is, in general, a complex number.

Substituting this assumed solution back into the differential equation, we obtain

$\gamma ^{2}+2\zeta \omega _{0}\gamma +\omega _{0}^{2}=0.\,$

Solving for γ, we find:

$\gamma =\omega _{0}(-\zeta \pm {\sqrt {\zeta ^{2}-1}}).$

System behavior

Dependence of the system behavior on the value of the damping ratio $\zeta$.

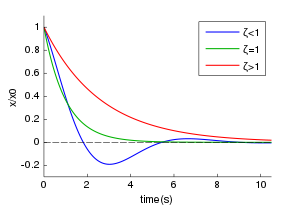
The behavior of the system depends on the relative values of the two fundamental parameters, the natural frequency ω₀ and the damping ratio ζ. In particular, the qualitative behavior of the system depends crucially on whether the quadratic equation for $\gamma$ has one real solution, two real solutions, or two complex conjugate solutions.

Critical damping

When ζ = 1, $\scriptstyle \gamma$ (defined above) is real, the system is said to be critically damped. An example of critical damping is the door-closer seen on many hinged doors in public buildings. Passenger cars' suspensions have damping ratios of approximately 0.25 or so to generate "soft" ride quality. When ride quality is ignored, for example in racing, damping ratios of 0.7 or more are frequently used. In the most extreme cases of very high-downforce racecars such as Formula 1, Champ Car, or IRL, one might see heavily overdamped ratios of up to 7.0 or 8.0 to control the aerodynamic platform.

In this case, the solution simplifies to:

$x(t)=(A+Bt)e^{-\omega _{0}t}\,$

where A and B are determined by the initial conditions of the system (usually the initial position and velocity of the mass):

$A=x(0)\,$

$B={\dot {x}}(0)+\omega _{0}x(0)\,$

Over-damping

When ζ > 1, $\scriptstyle \gamma$ is still real, but now the system is said to be over-damped. An over-damped door-closer will take longer to close than a critically damped door would.

The solution to the motion equation is:

$x(t)=Ae^{\gamma _{-}t}+Be^{\gamma _{+}t}$

where A and B are determined by the initial conditions of the system:

$A=x(0)-{\frac {\gamma _{-}x(0)-{\dot {x}}(0)}{\gamma _{-}-\gamma _{+}}}$

$B={\frac {\gamma _{-}x(0)-{\dot {x}}(0)}{\gamma _{-}-\gamma _{+}}}.$

Under-damping

Finally, when 0 ≤ ζ < 1, $\scriptstyle \gamma$ is complex, and the system is under-damped. In this situation, the system will oscillate at the natural damped frequency $\scriptstyle \omega _{\mathrm {d} }$, which is a function of the natural frequency and the damping ratio.

In this case, the solution can be generally written as:

$x(t)=e^{-\zeta \omega _{0}t}(A\cos(\omega _{\mathrm {d} }t)+B\sin(\omega _{\mathrm {d} }t))\,$

where

$\omega _{\mathrm {d} }=\omega _{0}{\sqrt {1-\zeta ^{2}}}\,$

represents the natural damped frequency of the system, and A and B are again determined by the initial conditions of the system:

$A=x(0)\,$

$B={\frac {1}{\omega _{\mathrm {d} }}}(\zeta \omega _{0}x(0)+{\dot {x}}(0)).\,$

For an under-damped system, the value of zeta can be found by examining the logarithm of the ratio of succeeding amplitudes of a system. This is called the Logarithmic Decrement. Zeta is expressed as:

Caption1

where x₀ is the initial peak amplitude, x_n is the amplitude of the peak being examined, and n is how many periods separate these peaks. This is illustrated in the following graph: Logarithmic decrement.jpg

Alternative models

Viscous damping models, although widely used, are not the only damping models. A wide range of models can be found in specialized literature, but one of them should be referred here: the so called "hysteretic damping model" or "structural damping model".

When a metal beam is vibrating, the internal damping can be better described by a force proportional to the displacement but in phase with the velocity. In such case, the differential equation that describes the free movement of a single-degree-of-freedom system becomes:

$m{\ddot {x}}+hxi+kx=0$

where h is the hysteretic damping coefficient and i denotes the imaginary unit; the presence of i is required to synchronize the damping force to the velocity ( xi being in phase with the velocity). This equation is more often written as:

$m{\ddot {x}}+k(1+i\eta )x=0$

where η is the hysteretic damping ratio, that is, the fraction of energy lost in each cycle of the vibration.

Although requiring complex analysis to solve the equation, this model reproduces the real behaviour of many vibrating structures more closely than the viscous model.

See also: Friction and Drag

See also

• Damping ratio
• Damping factor
• RLC circuit
• Oscillator
• Harmonic oscillator
• Simple harmonic motion
• Resonance
• Impulse excitation technique
• Audio system measurements
• Tuned mass damper
• Vehicle suspension
• Vibration

External links

• Calculation of the matching attenuation,the damping factor, and the damping of bridging

• A-level Physics experiment on the subject of Damped Harmonic Motion with solution curve graphs