Trilinear interpolation

Trilinear interpolation is a method of multivariate interpolation on a 3-dimensional grid (possibly with an arbitrary, non-overlapping grid points in each dimension, but i.e. not an arbitrarily triangularized finite element mesh) of discretely sampled data. It approximates the value of an intermediate point $(x,y,z)$ within the local axial rectangular prism linearly, using data on the lattice points.

Trilinear interpolation is frequently used in numerical analysis, data analysis, and computer graphics.

Compared to linear and bilinear interpolation

Trilinear interpolation is the extension of linear interpolation, which operates in spaces with dimension $D=1$, and bilinear interpolation, which operates with dimension $D=2$, to dimension $D=3$. The order of accuracy is 1 for all these interpolation schemes, and it requires $(1+n)^{D}=8$ adjacent pre-defined values surrounding the interpolation point. There are several ways to arrive at trilinear interpolation, it is equivalent to 3-dimensional tensor B-spline interpolation of order 1, and the trilinear interpolation operator is also a tensor product of 3 linear interpolation operators

Example

On a periodic and cubic lattice with spacing 1, let $x_{d}$, $y_{d}$, and $z_{d}$ be the differences to the largest integer smaller than each of $x$, $y$, $z$, that is:

$x_{d}=x-\lfloor x\rfloor$

$y_{d}=y-\lfloor y\rfloor$

$z_{d}=z-\lfloor z\rfloor$

Eight corner points on a cube surrounding the interpolation point C

Depiction of 3D interpolation

First we interpolate along $z$, giving:

$i_{1}=v[\lfloor x\rfloor ,\lfloor y\rfloor ,\lfloor z\rfloor ]\times (1-z_{d})+v[\lfloor x\rfloor ,\lfloor y\rfloor ,\lceil z\rceil ]\times z_{d}$

$i_{2}=v[\lfloor x\rfloor ,\lceil y\rceil ,\lfloor z\rfloor ]\times (1-z_{d})+v[\lfloor x\rfloor ,\lceil y\rceil ,\lceil z\rceil ]\times z_{d}$

$j_{1}=v[\lceil x\rceil ,\lfloor y\rfloor ,\lfloor z\rfloor ]\times (1-z_{d})+v[\lceil x\rceil ,\lfloor y\rfloor ,\lceil z\rceil ]\times z_{d}$

$j_{2}=v[\lceil x\rceil ,\lceil y\rceil ,\lfloor z\rfloor ]\times (1-z_{d})+v[\lceil x\rceil ,\lceil y\rceil ,\lceil z\rceil ]\times z_{d}.$

Then we interpolate these values (along $y$), giving:

$\ w_{1}=i_{1}(1-y_{d})+i_{2}y_{d}$

$\ w_{2}=j_{1}(1-y_{d})+j_{2}y_{d}$

Finally we interpolate these values along $x$:

$\ IV=w_{1}(1-x_{d})+w_{2}x_{d}.$

This gives us a predicted value for the point.

The result of trilinear interpolation is independent of the order of the successive interpolation steps, that is, performing the linear interpolations in another order of dimensions, along $x$, along $y$, then along $z$, produces an identical expression for the predicted value.

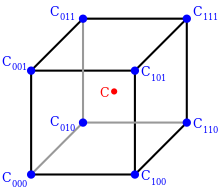
The above operations can be visualized as follows: First we find the eight corners of a cube that surround our point of interest. These corners have the values C000, C100, C010, C110, C001, C101, C011, C111.

Next, we perform linear interpolation between C000 and C100 to find C00, C001 and C101 to find C01, C011 and C111 to find C11, C010 and C110 to find C10.

Now we do interpolation between C00 and C10 to find C0, C01 and C11 to find C1. Finally, we calculate the value C via linear interpolation of C0 and C1

C++ Implementation

//Note: x, y, z in local coordinates [0,h] where h is the width of a cell.
float triLin(float x, float y, float z, float h, float _000, float _100, float _010, float _001, float _101, float _011, float _110, float _111){
	float scale = 1/h;
	h = scale * h;
	x = scale * x;
	y = scale * y;
	z = scale * z;
	float val;
		float i1 = _000 * (1-z) + _010 * (z);
		float i2 = _001 * (1-z) + _011 * (z);
		float j1 = _100 * (1-z) + _110 * (z);
		float j2 = _101 * (1-z) + _111 * (z);
		float w1 = i1 * (1 - y) + i2 * y;
		float w2 = j1 * (1 - y) + j2 * y;
		val = w1 * (1-x) + w2 * x;
	return val;
}

See also

• Linear interpolation
• Bilinear interpolation
• Tricubic interpolation

External links

• pseudo-code
• Paul Bourke, Interpolation methods, 1999. Contains a section on trilinear interpolation.