Eddy covariance

The eddy covariance (also known as eddy correlation and eddy flux) technique is a key atmospheric flux measurement technique to measure and calculate vertical turbulent fluxes within atmospheric boundary layers. It is a statistical method used in meteorology and other applications that analyzes high-frequency wind and scalar atmospheric data series, and yields values of fluxes of these properties. Such flux measurements are widely used to estimate momentum, heat, water, and carbon dioxide exchange, as well as exchange of methane and other trace gases [1] [2] [3] [4].
The technique is also used extensively for verification and tuning of global climate models, mesoscale and weather models, complex biogeochemical and ecological models, and remote sensing estimates from satellites and aircraft. The technique is mathematically complex, and requires significant care in setting up and processing data. To date, there is no uniform terminology or a single methodology for the Eddy Covariance technique, but much effort is being made by flux measurement networks (e.g., Fluxnet, Ameriflux, ICOS, CarboEurope, Fluxnet Canada, NEON, and iLEAPS) to unify the various approaches.
General principles
Representation of the air flow in the atmospheric boundary layer
Air flow can be imagined as a horizontal flow of numerous rotating eddies, that is, turbulent vortices of various sizes, with each eddy having horizontal and vertical components. The situation looks chaotic, but vertical movement of the components can be measured from the tower.
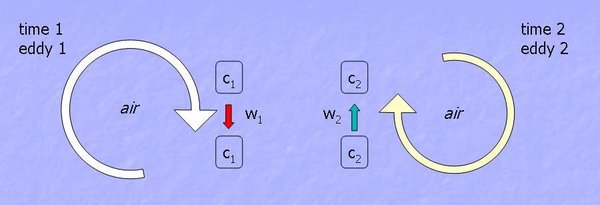
Physical meaning of the eddy covariance method
At one physical point on the tower, at Time1, Eddy1 moves parcel of air c1 down at the speed w1. Then, at Time2, Eddy2 moves parcel c2 up at the speed w2. Each parcel has a concentration, temperature, and humidity. If these factors, along with the speed are known, we can determine the flux. For example, if one knew how many molecules of water went down with eddies at Time 1, and how many molecules went up with eddies at Time2, at the same point, one could calculate the vertical flux of water at this point over this time. So, vertical flux can be presented as a covariance of the vertical wind velocity and the concentration of the entity of interest.
Mathematical foundation
In mathematical terms, "eddy flux" is computed as a covariance between instantaneous deviation in vertical wind speed (w') from the mean value (w-overbar) and instantaneous deviation in gas concentration, mixing ratio (s'), from its mean value (s-overbar), multiplied by mean air density (ρa). Several mathematical operations and assumptions, including Reynolds decomposition, are involved in getting from physically complete equations of the turbulent flow to practical equations for computing "eddy flux", as shown below.


Major assumptions
- Measurements at a point can represent an upwind area
- Measurements are done inside the boundary layer of interest
- Fetch/flux footprint is adequate – fluxes are measured only at area of interest
- Flux is fully turbulent – most of the net vertical transfer is done by eddies
- Terrain is horizontal and uniformed: average of fluctuations is zero; density fluctuations negligible; flow convergence & divergence negligible
- Instruments can detect very small changes at high frequency, ranging from minimum of 5 Hz and to 40 Hz for tower-based measurements
Eddy covariance processing software
Currently (2011) there are many software programs [5] to process eddy covariances data and derive quantities such as heat, momentum, and gas fluxes. The programs range significantly in complexity, flexibility, number of allowed instruments and variables, help system and user support. Some programs are open-source software, while others are closed-source or proprietary.
Examples include free fully supported and documented open-source software such as EddyPro; free unsupported open-source programs such as ECO2S and ECpack; free closed-source packages such as EdiRe, TSA, TK2, Alteddy, and EddySoft. Eddy covariance processing algorithms can also be implemented in commercial software such as Matlab.
Summary
In a nutshell, the 3D wind and another variable (usually gas concentration, temperature or momentum) are decomposed into mean and fluctuating components. The covariance is calculated between the fluctuating component of the vertical wind and the fluctuating component of gas concentration. The measured flux is proportional to the covariance.
The area from which the detected eddies originate is described probabilistically and called a flux footprint. The flux footprint area is dynamic in size and shape, changing with wind direction, thermal stability and measurements height, and has a gradual border.
The effect of sensor separation, finite sampling length, sonic path averaging, as well as other instrumental limitations, affect frequency response of the measurement system and may need a co-spectral correction, especially noticeable with closed-path instruments and at low heights below 1-1.5 m.
See also
- Eddy
- Ecosystem respiration
- Evaporation
- Evapotranspiration
- Greenhouse gas emissions
- Heat flux
- FluxNet
- Latent heat flux
- Transpiration
References
- ^ Baldocchi, D., B. Hicks, and T. Meyers. 1988. Measuring biosphere-atmosphere exchanges of biologically related gases with micrometeorological methods. Ecology 69, 1331-1340
- ^ Verma, S.B.: 1990, Micrometeorological methods for measuring surface fluxes of mass and energy, Remote Sensing Reviews 5(1): 99-115
- ^ Lee, X., W. Massman, and B. Law. 2004. Handbook of Micrometeorology. Kluwer Academic Publishers, The Netherlands, 250 pp.
- ^ Burba, G.G., and D.J. Anderson, 2010. A Brief Practical Guide to Eddy Covariance Flux Measurements: Principles and Workflow Examples for Scientific and Industrial Applications. LI-COR Biosciences, Lincoln, USA, 211 pp.
- ^ M. Mauder, T. Foken, R. Clement, J. A. Elbers, W. Eugster, T. Grunwald, B. Heusinkveld, and O. Kolle. 2007. Quality control of CarboEurope flux data – Part II: Inter-comparison of eddy-covariance software, Biogeosciences Discuss., 4, 4067–4099
Further reading
- Burba, G.G., and D.J. Anderson, 2010. A Brief Practical Guide to Eddy Covariance Flux Measurements: Principles and Workflow Examples for Scientific and Industrial Applications. LI-COR Biosciences, Lincoln, USA, 211 pp.
- Foken, T. 2008. Micrometeorology, Springer-Verlag, Berlin, Germany, 308 pp.
- Lee, X., W. Massman, and B. Law. 2004. Handbook of Micrometeorology. Kluwer Academic Publishers, The Netherlands, 250 pp.
