Cone
- Not to be confused with the conical surface. For other uses, see cone (disambiguation).
This article needs additional citations for verification. (October 2009) |
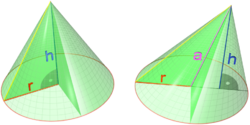
A cone is an -dimensional geometric shape that tapers smoothly from a base (usually flat and circular) to a point called the apex or vertex.
Formally, it is the solid figure formed by the locus of all straight line segments that join the apex to the base. The term "cone" is sometimes used to refer to the surface or the lateral surface of this solid figure (the lateral surface of a cone is equal to the surface minus the base).
The axis of a cone is the straight line (if any), passing through the apex, about which the base has a rotational symmetry.
In common usage in elementary geometry, cones are assumed to be right circular, where right means that the axis passes through the centre of the base (suitably defined) at right angles to its plane, and circular means that the base is a circle. Contrasted with right cones are oblique cones, in which the axis does not pass perpendicularly through the centre of the base.[1] In general, however, the base may be any shape, and the apex may lie anywhere (though it is often assumed that the base is bounded and has finite area, and that the apex lies outside the plane of the base). For example, a pyramid is technically a cone with a polygonal base.
Other mathematical meanings
In mathematical usage, the word "cone" is used also for an 'infinite cone', the union of a set of half-lines that start at a common apex point and go through a base. Observe that an infinite cone is not bounded by its base and extends to infinity. A 'doubly infinite cone', or 'double cone', is the union of a set of straight lines that pass through a common apex point and go through a base, therefore double infinite cones extend symmetrically on both sides of the apex.
The boundary of an infinite or doubly infinite cone is a conical surface, and the intersection of a plane with this surface is a conic section. For infinite cones, the word axis again usually refers to the axis of rotational symmetry (if any). Either half of a double cone on one side of the apex is called a 'nappe'.
Depending on the context, "cone" may also mean specifically a convex cone or a projective cone.
Also, an oblique shaped cone is known as a circular based pyramid due to the inwardly converging hypos towards the apex point.
Further terminology
The perimeter of the base of a cone is called the 'directrix', and each of the line segments between the directrix and apex is a 'generatrix' of the lateral surface. (For the connection between this sense of the term "directrix" and the directrix of a conic section, see Dandelin spheres.)
The 'base radius' of a circular cone is the radius of its base; often this is simply called the radius of the cone. The aperture of a right circular cone is the maximum angle between two generatrix lines; if the generatrix makes an angle θ to the axis, the aperture is 2θ.
A cone with its apex cut off by a plane is called a "truncated cone"; if the truncation plane is parallel to the cone's base, it is called a frustum. An 'elliptical cone' is a cone with an elliptical base. A 'generalized cone' is the surface created by the set of lines passing through a vertex and every point on a boundary (also see visual hull).
none
Projective geometry

In projective geometry, a cylinder is simply a cone whose apex is at infinity. Intuitively, if one keeps the base fixed and takes the limit as the apex goes to infinity, one obtains a cylinder, the angle of the side increasing as arctan, in the limit forming a right angle.
This is useful in the definition of degenerate conics, which require considering the cylindrical conics.
See also
References
External links
- Weisstein, Eric W. "Generalized Cone". MathWorld.
- Spinning Cone from Math Is Fun
- Paper model cone
- Lateral surface area of an oblique cone
- Cut a Cone An interactive demonstration of the intersection of a cone with a plane

