Alpha algorithm

The α-algorithm or α-miner is an algorithm used in process mining, aimed at reconstructing causality from a set of sequences of events. It was first put forward by van der Aalst, Weijters and Măruşter. The goal of Alpha miner is to convert the event log into a workflow-net based on the relations between various activities in the event log. An event log is a multi-set of traces, and a trace is a sequence of activity names. Several extensions or modifications of it have since been presented, which will be listed below.

Alpha miner was the first process discovery algorithm ever proposed, and it gives a good overview of the aim of process discovery and how various activities within the process are executed. Alpha miner was also the basis for the development of many other process mining techniques such as heuristic miner, genetic mining was developed based on the idea alpha miner is built on.

Short description

The algorithm takes a workflow log $W\subseteq T^{*}$ as input and results in a workflow net being constructed.

It does so by examining causal relationships observed between tasks. For example, one specific task might always precede another specific task in every execution trace, which would be useful information.

Definitions used

• A workflow trace or execution trace is a string over an alphabet $T$ of tasks.
• A workflow log is a set of workflow traces.

Event log

Event log is the primary requirement for applying any process discovery algorithm. An event log consists of a unique identifier for a case, activity name describing the action occurring in the process and timestamp. An event log can be represented as a multi-set of activities. For the sake of simplicity the following example would use alphabetic letter to represent an activity. Consider an example event log shown in the following figure:

Sample event log

Case id	Activity	Timestamp
1	A	2019/10/09 14:50:17.000
1	B	2019/10/09 15:50:17.000
1	C	2019/10/09 15:56:17.000
1	D	2019/10/10 13:50:17.000
2	A	2019/10/10 14:30:17.000
2	C	2019/10/10 14:50:14.000
2	B	2019/10/11 09:50:17.000
2	D	2019/10/11 10:50:17.000
3	A	2019/10/11 12:50:17.000
3	E	2019/10/21 14:50:17.000
3	D	2019/10/21 15:50:17.000

An event log is a multi set of traces, and a trace is a sequence of activities. Thus, an event log such as above can be represented using the following notation:

$L1=[<A,B,C,D>,<A,C,B,D>,<A,E,D>]$

Every event log can be boiled down into a multi-set of traces, and such traces can be further used to break down relationships between various activities in the process. According to the rules of alpha miner, activities belonging to various cases can have 4 types of relationships between them:

• Direct Succession: x > y if and only if some relation x is directly following by y. In our example, we can consider that A > B, A > E, A > C.
• Causality: x → y iff x > y and not y > x. In our example, we can consider that A → E.
• Parallel: x || y iff x > y and y > x. In our example, we have B || C.
• Choice: x # y iff not(x > y) and not(y > x). In our example, we have A # D.

Patterns

Sequence Pattern: A → B XOR-split Pattern: A → B, A → C, and B # C

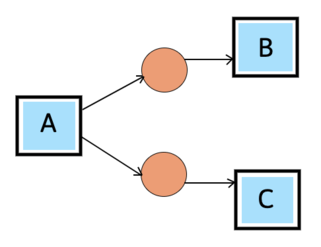AND-split Pattern: A → B, A → C, and B || C

Description

The alpha miner starts with converting an event log into directly-follows, sequence, parallel, and choice relations, and using them to create a petri net describing the process model. Initially the algorithm constructs a footprint matrix. Using the footprint matrix and the above shown pattern, one can construct a process model. Based on the four relations described earlier a footprint based matrix is first discovered. Using the footprint based matrix places are discovered. Each place is identified with a pair of sets of tasks, in order to keep the number of places low.

Footprint matrix for the log L1

	a	b	c	d	e
a	#	→	→	#	→
b	←	#	||	→	#
c	←	||	#	→	#
d	#	←	←	#	←
e	←	#	#	→	#

• $Y_{W}$ is the set of all pairs $(A,B)$ of maximal sets of tasks such that
  • Neither $A\times A$ and $B\times B$ contain any members of > and
  • $A\times B$ is a subset of →
• $P_{W}$ contains one place $p_{(A,B)}$ for every member of $Y_{W}$, plus the input place $i_{W}$ and the output place $o_{W}$

The flow relation $F_{W}$ is the union of the following:

• $\{(a,p_{(A,B)})|(A,B)\in Y_{W}\wedge a\in A\}$
• $\{(p_{(A,B)},b)|(A,B)\in Y_{W}\wedge b\in B\}$
• $\{(i_{W},t)|t\in T_{I}\}$
• $\{(t,i_{O})|t\in T_{O}\}$

The result is

• a Petri net structure $\alpha (W)=(P_{W},T_{W},F_{W})$
• with one input place $i_{W}$ and one output place $o_{W}$
• because every transition of $T_{W}$ is on a $F_{W}$-path from $i_{W}$ to $o_{W}$, it is indeed a workflow net.

For the example given above, the following petri net would be resultant of the application of alpha miner.

Properties

It can be shown that in the case of a complete workflow log generated by a sound SWF net, the net generating it can be reconstructed. Complete means that its $\succ _{W}$ relation is maximal. It is not required that all possible traces be present (which would be countably infinite for a net with a loop).

Limitations

• Implicit places: Alpha miner cannot distinguish between implicit and required places and thus might result in additional non required places in the discovered petri net.
• Loops: Alpha miner cannot discover loops of the length 1 and 2 in the process model.
• Local dependencies are often missed in alpha miner.
• Representational bias: Alpha miner can only discover petri net thus adding representational bias such as requirement on unique visible labels for every transition.