Jemmis mno rules
This article has multiple issues. Please help improve it or discuss these issues on the talk page. (Learn how and when to remove these messages)
|
In chemistry, the Jemmis mno rules represent a unified rule for predicting and systematizing structures of compounds, usually clusters. The rules involve electron counting. They were formulated by E. D. Jemmis to explain the structures of condensed polyhedral boranes such as B20H16, which are obtained by condensing polyhedral boranes by sharing a triangular face, an edge, a single vertex, or four vertices. These rules are additions and extensions to Wade's rules and polyhedral skeletal electron pair theory.[1][2] The Jemmis mno rule provides the relationship between polyhedral boranes, condensed polyhedral boranes, and β-rhombohedral boron.[3][4] This is similar to the relationship between benzene, condensed benzenoid aromatics, and graphite, shown by Hückel's 4n + 2 rule, as well as the relationship between tetracoordinate tetrahedral carbon compounds and diamond. The Jemmis mno rules reduce to Hückel's rule when restricted to two dimensions and reduce to Wade's rules when restricted to one polyhedron.[5]
Electron-counting rules
[edit]Electron-counting rules are used to predict the preferred electron count for molecules. The octet rule, the 18-electron rule, and Hückel's 4n + 2 pi-electron rule are proven to be useful in predicting the molecular stability. Wade's rules were formulated to explain the electronic requirement of monopolyhedral borane clusters. The Jemmis mno rules are an extension of Wade's rules, generalized to include condensed polyhedral boranes as well.
The first condensed polyhedral borane, B20H16, is formed by sharing four vertices between two icosahedra. According to Wade's n + 1 rule for n-vertex closo structures, B20H16 should have a charge of +2 (n + 1 = 20 + 1 = 21 pairs required; 16 BH units provide 16 pairs; four shared boron atoms provide 6 pairs; thus 22 pairs are available). To account for the existence of B20H16 as a neutral species, and to understand the electronic requirement of condensed polyhedral clusters, a new variable, m, was introduced and corresponds to the number of polyhedra (sub-clusters).[6] In Wade's n + 1 rule, the 1 corresponds to the core bonding molecular orbital (BMO) and the n corresponds to the number of vertices, which in turn is equal to the number of tangential surface BMOs. If m polyhedra condense to form a macropolyhedron, m core BMOs will be formed. Thus the skeletal electron pair (SEP) requirement of closo-condensed polyhedral clusters is m + n.
Single-vertex sharing is a special case where each subcluster needs to satisfy Wade's rule separately. Let a and b be the number of vertices in the subclusters including the shared atom. The first cage requires a + 1 and the second cage requires b + 1 SEPs. Therefore, a total of a + b + 2 or a + b + m SEPs are required; but a + b = n + 1, as the shared atom is counted twice. The rule can be modified to m + n + 1, or generally m + n + o, where o corresponds to the number of single-vertex sharing condensations. The rule can be made more general by introducing a variable, p, corresponding to the number of missing vertices, and q, the number of caps. As such, the generalized Jemmis rule can be stated as follows:
- The SEP requirement of condensed polyhedral clusters is m + n + o + p − q, where m is the number of subclusters, n is the number of vertices, o is the number of single-vertex shared condensations, p is the number of missing vertices and q is the number of caps.[4][7]
Examples
[edit]B20H16
[edit]
m + n + o + p − q = 2 + 20 + 0 + 0 + 0 = 22 SEPs are required; 16 BH units provide 16 pairs; four shared boron atoms provide 6 pairs, which describes why B20H16 is stable as a neutral species.[7]
B21H−
18
[edit]closo-B21H−18 is formed by the face-sharing condensation of two icosahedra. The m + n + o + p − q rule demands 23 SEPs; 18 BH units provide 18 pairs and 3 shared boron atoms provide 4+1⁄2 pairs; the negative charge provides one half pair.[8]
B12H16
[edit]The bis-nido-B12H16 is formed by the edge-sharing condensation of a nido-B8 unit and a nido-B6 unit. The m + n + o + p − q count of 16 SEPs are satisfied by ten BH units which provide 10 pairs, two shared boron atoms which provide 3 pairs, and six bridging H atoms which provide 3 pairs.[7]
Cu(B11H11)3−
2
[edit]m + n + o + p − q = 26 SEPs. A transition metal with n valence electrons provides n − 6 electrons for skeletal bonding as 6 electrons occupying the metal-like orbitals do not contribute much to the cluster bonding. Therefore Cu provides 2+1⁄2 pairs, 22 BH units provide 22 pairs; three negative charges provide 1+1⁄2 pairs.[7]
Ferrocene
[edit]
According to the m + n + o + p − q rule, ferrocene requires 2 + 11 + 1 + 2 − 0 = 16 SEPs. 10 CH units provide 15 pairs while Fe provides one pair. [7]
B18H2−
20
[edit]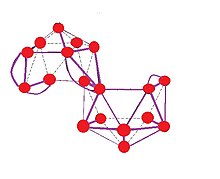
B18H2−20 is a bis-nido edge-shared polyhedron. Here, m + n + o + p − q = 2 + 18 + 0 + 2 − 0 = 22; 16 BH units provide 16 pairs, 4 bridging hydrogen atoms provide 2 pairs, two shared boron atoms provide 3 pairs, along with the two negative charges which provide 1 pair.[7]
Triple-decker complexes
[edit]Triple-decker complexes are known to obey a 30-valence electron (VE) rule. Subtracting 6 pairs of nonbonding electrons from the two metal atoms brings the number of SEPs to 9 pairs. For a triple-decker complex with C5H5 as the decks, m + n + o + p − q = 3 + 17 + 2 + 2 − 0 = 24. Subtracting the 15 pairs corresponding to C–C sigma bonds, it becomes 9 pairs. For example, consider (C5(CH3)5)3Ru+2: 15 C–CH3 groups provide 22+1⁄2 pairs. Each ruthenium atom provides one pair. Removing the electron corresponding to the positive charge of the complex leads to a total of 22+1⁄2 + 2 − 1⁄2 = 24 pairs.
β-Rhombohedral boron
[edit]
The structure of β-rhombohedral boron is complicated by the presence of partial occupancies and vacancies.[9][10][11] The idealized unit cell, B105 has been shown to be electron-deficient and hence metallic according to theoretical studies, but β-boron is a semiconductor.[12] Application of the Jemmis rule shows that the partial occupancies and vacancies are necessary for electron sufficiency.
B105 can be conceptually divided into a B48 fragment and a B28−B−B28 (B57) fragment. According to Wade's rule, the B48 fragment requires 8 electrons (the icosahedron at the centre (green) requires 2 electrons; each of the six pentagonal pyramids (black and red) completes an icosahedron in the extended structure; as such the electronic requirement for each of them is 1). The B28−B−B28 or B57 is formed by the condensation of 6 icosahedra and two trigonal bipyramids. Here, m + n + o + p − q = 8 + 57 + 1 + 0 − 0 = 66 pairs required for stability, but 67+1⁄2 are available. Therefore the B28−B−B28 fragment has 3 excess electrons and the idealized B105 is missing 5 electrons. The 3 excess electrons in the B28−B−B28 fragment can be removed by removing one B atom, which leads to B27−B−B28 (B56). The requirement of 8 electrons by the B48 fragment can be satisfied by 2+2⁄3 boron atoms and the unit cell contains 48 + 56 + 2+2⁄3 = 106+2⁄3, which is very close to the experimental result.[3]
References
[edit]- ^ Wade, K. (1971). "The structural significance of the number of skeletal bonding electron-pairs in carboranes, the higher boranes and borane anions, and various transition-metal carbonyl cluster compounds". J. Chem. Soc. D (15): 792. doi:10.1039/c29710000792.
- ^ Mingos, D. M. P (1984). "Polyhedral skeletal electron pair approach". Acc. Chem. Res. 17 (9): 311–319. doi:10.1021/ar00105a003.
- ^ a b Jemmis, E. D.; Balakrishnarajan, M. M. (2001). "Polyhedral Boranes and Elemental Boron: Direct Structural Relations and Diverse Electronic Requirements". J. Am. Chem. Soc. 123 (18): 4324–4330. doi:10.1021/ja0026962. PMID 11457199.
- ^ a b Jemmis, E. D.; Balakrishnarajan, M. M.; Pancharatna, P. D. (2001). "A Unifying Electron-Counting Rule for Macropolyhedral Boranes, Metallaboranes, and Metallocenes". J. Am. Chem. Soc. 123 (18): 4313–4323. doi:10.1021/ja003233z. PMID 11457198.
- ^ Jemmis, E. D.; Jayasree, E. G. (2003). "Analogies between Boron and Carbon". Acc. Chem. Res. 36 (11): 816–824. doi:10.1021/ar0300266. PMID 14622028.
- ^ Jemmis, E. D.; Balakrishnarajan, M. M. (2000). "Electronic Requirements of Polycondensed Polyhedral Boranes". J. Am. Chem. Soc. 122 (18): 4516–4517. doi:10.1021/ja994199v.
- ^ a b c d e f Jemmis, E. D.; Balakrishnarajan, M. M.; Pancharatna, P. D. (2002). "Electronic Requirements for Macropolyhedral Boranes". Chem. Rev. 102 (1): 93–144. doi:10.1021/cr990356x. PMID 11782130.
- ^ Bernhardt, E.; Brauer, D. J.; Finze, M.; Willner, H. (2007). "closo-[B21H18]−: A Face-Fused Diicosahedral Borate Ion". Angew. Chem. Int. Ed. Engl. 46 (16): 2927–2930. doi:10.1002/anie.200604077. PMID 17366499.
- ^ Hughes, R. E.; Kennard, C. H. L.; Sullenger, D. B.; Weakliem, H. A.; Sands, D. E.; Hoard, J. L. (1963). "The Structure of β-Rhombohedral Boron". J. Am. Chem. Soc. 85 (3): 361–362. doi:10.1021/ja00886a036.
- ^ Hoard, J. L.; Sullenger, D. B.; Kennard, C. H. L.; Hughes, R. E. (1970). "The structure analysis of β-rhombohedral boron". J. Solid State Chem. 1 (2): 268–277. Bibcode:1970JSSCh...1..268H. doi:10.1016/0022-4596(70)90022-8.
- ^ Slack, G. A.; Hejna, C. I.; Garbauskas, M. F.; Kasper, J. S. (1988). "The crystal structure and density of β-rhombohedral boron". J. Solid State Chem. 76 (1): 52–63. Bibcode:1988JSSCh..76...52S. doi:10.1016/0022-4596(88)90192-2.
- ^ Prasad, D. L. V. K; Balakrishnarajan, M. M.; Jemmis, E. D. (2005). "Electronic structure and bonding of β-rhombohedral boron using cluster fragment approach". Phys. Rev. B. 72 (19): 195102. Bibcode:2005PhRvB..72s5102P. doi:10.1103/physrevb.72.195102.



