Himmelblau's function
Appearance
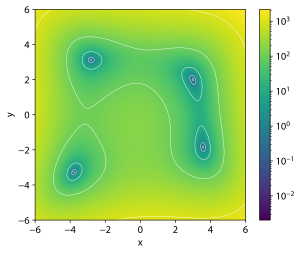
In mathematical optimization, Himmelblau's function is a multi-modal function, used to test the performance of optimization algorithms. The function is defined by:
It has one local maximum at and where , and four identical local minima:
The locations of all the minima can be found analytically. However, because they are roots of quartic polynomials, when written in terms of radicals, the expressions are somewhat complicated.[citation needed]
The function is named after David Mautner Himmelblau (1924–2011), who introduced it.[1]
See also
[edit]References
[edit]- ^ Himmelblau, D. (1972). Applied Nonlinear Programming. McGraw-Hill. ISBN 0-07-028921-2.