Kempe chain

A graph containing a Kempe chain consisting of alternating blue and red vertices

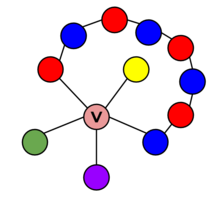
In mathematics, a Kempe chain is a device used mainly in the study of the four colour theorem. Intuitively, it is a connected chain of points on a graph with alternating colors.

History

Kempe chains were first used by Alfred Kempe in his attempted proof of the four colour theorem. Even though his proof turned out to be incomplete, the method of Kempe chains is crucial to the successful modern proofs (Appel & Haken, Robertson et al., etc.). Furthermore, the method is used in the proof of the five-colour theorem, a weaker form of the four-colour theorem.

Formal definition

The term "Kempe chain" is used in two different but related ways.

Suppose G is a graph with vertex set V, and we are given a colouring function

$c:V\to S$

where S is a finite set of colours, containing at least two distinct colours a and b. If v is a vertex with colour a, then the (a, b)-Kempe chain of G containing v is the maximal connected subset of V which contains v and whose vertices are all coloured either a or b.

The above definition is what Kempe worked with. Typically the set S has four elements (the four colours of the four colour theorem), and c is a proper colouring, that is, each pair of adjacent vertices in V are assigned distinct colours.

A more general definition, which is used in the modern computer-based proofs of the four colour theorem, is the following. Suppose again that G is a graph, with edge set E, and this time we have a colouring function

$c:E\to S.$

If e is an edge assigned colour a, then the (a, b)-Kempe chain of G containing e is the maximal connected subset of E which contains e and whose edges are all coloured either a or b.

This second definition is typically applied where S has three elements, say a, b and c, and where V is a cubic graph, that is, every vertex has three incident edges. If such a graph is properly coloured, then each vertex must have edges of three distinct colours, and Kempe chains end up being paths, which is simpler than in the case of the first definition.

Application to the four colour theorem

Main article: Four color theorem

In the four color theorem, Kempe was able to prove that all graphs necessarily have a vertex of five or less, or containing a vertex that touches five other vertices, called its neighbors. As such, to prove the four color theorem, Kempe could prove that vertices of five or less were all four-colorable. Kempe was able to prove the case of degree four and give a partial proof of degree five using Kempe chains.

In this case, Kempe chains are used to prove the idea that no vertex has to be touching four colors different from itself, i.e having a degree of 4. First, one can create a graph with a vertex v and four vertices as neighbors. If we remove the vertex v, we can four-color the remaining vertices. We can set the colors as (in clockwise order) red, yellow, blue, and green. In this situation, there can be a Kempe chain joining the red and blue neighbors or a Kempe chain joining the green and yellow neighbors, but not both, since these two paths would necessarily intersect, and the vertex where they intersect cannot be colored. Supposing that the Kempe chain is connecting the green and yellow neighbors, red and blue must then necessarily not have a Kempe chain between them. So, when placing the original vertex v back into the graph, we can simply reverse the colors of the red vertex and its neighbors (including the red vertex, making it blue) and coloring vertex v as red. This results in a four-colored graph.

Other Applications

Kempe chains have been used to solve problems in coloring extension.