Lifting property

In mathematics, in particular in category theory, the lifting property is a property of a pair of morphisms in a category. It is used in homotopy theory within algebraic topology to define properties of morphisms starting from an explicitly given class of morphisms. It appears in a prominent way in the theory of model categories, an axiomatic framework for homotopy theory introduced by Daniel Quillen. It is also used in the definition of a factorization system, and of a weak factorization system, notions related to but less restrictive than the notion of a model category. Several elementary notions may also be expressed using the lifting property starting from a list of (counter)examples.

Formal definition

A morphism i in a category has the left lifting property with respect to a morphism p, and p also has the right lifting property with respect to i, sometimes denoted $i\perp p$ or $i\downarrow p$ , iff the following implication holds for each morphism f and g in the category:

if the outer square of the following diagram commutes, then there exists h completing the diagram, i.e. for each $f:A\to X$ and $g:B\to Y$ such that $p\circ f=g\circ i$ there exists $h:B\to X$ such that $h\circ i=f$ and $p\circ h=g$ .

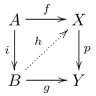
This is sometimes also known as the morphism i being orthogonal to the morphism p; however, this can also refer to the stronger property that whenever f and g are as above, the diagonal morphism h exists and is also required to be unique.

For a class C of morphisms in a category, its left orthogonal $C^{\perp \ell }$ or $C^{\perp }$ with respect to the lifting property, respectively its right orthogonal $C^{\perp r}$ or ${}^{\perp }C$ , is the class of all morphisms which have the left, respectively right, lifting property with respect to each morphism in the class C. In notation,

{\begin{aligned}C^{\perp \ell }&:=\{i\mid \forall p\in C,i\perp p\}\\C^{\perp r}&:=\{p\mid \forall i\in C,i\perp p\}\end{aligned}}

Taking the orthogonal of a class C is a simple way to define a class of morphisms excluding non-isomorphisms from C, in a way which is useful in a diagram chasing computation.

Thus, in the category Set of sets, the right orthogonal $\{\emptyset \to \{*\}\}^{\perp r}$ of the simplest non-surjection $\emptyset \to \{*\},$ is the class of surjections. The left and right orthogonals of $\{x_{1},x_{2}\}\to \{*\},$ the simplest non-injection, are both precisely the class of injections,

\{\{x_{1},x_{2}\}\to \{*\}\}^{\perp \ell }=\{\{x_{1},x_{2}\}\to \{*\}\}^{\perp r}=\{f\mid f{\text{ is an injection }}\}.

It is clear that $C^{\perp \ell r}\supset C$ and $C^{\perp r\ell }\supset C$ . The class $C^{\perp \ell }$ is always closed under retracts, pullbacks, (small) products (whenever they exist in the category) and composition of morphisms, and contains all isomorphisms of C. Meanwhile, $C^{\perp r}$ is closed under retracts, pushouts, (small) coproducts and transfinite composition (filtered colimits) of morphisms (whenever they exist in the category), and also contains all isomorphisms.

Examples

A number of notions can be defined by passing to the left or right orthogonal several times starting from a list of explicit examples, i.e. as $C^{\perp \ell },C^{\perp r},C^{\perp \ell r},C^{\perp \ell \ell }$ , where $C$ is a class consisting of several explicitly given morphisms. A useful intuition is to think that the property of left-lifting against a class C is a kind of negation of the property of being in C, and that right-lifting is also a kind of negation. Hence the classes obtained from C by taking orthogonals an odd number of times, such as $C^{\perp \ell },C^{\perp r},C^{\perp \ell r\ell },C^{\perp \ell \ell \ell }$ etc., represent various kinds of negation of C, so $C^{\perp \ell },C^{\perp r},C^{\perp \ell r\ell },C^{\perp \ell \ell \ell }$ each consists of morphisms which are far from having property $C$ .

Examples of lifting properties in algebraic topology

A map $f:U\to B$ has the path lifting property iff $\{0\}\to [0,1]\perp f$ where $\{0\}\to [0,1]$ is the inclusion of one end point of the closed interval into the interval $[0,1]$ .

A map $f:U\to B$ has the homotopy lifting property iff $X\to X\times [0,1]\perp f$ where $X\to X\times [0,1]$ is the map $x\mapsto (x,0)$ .

Examples of lifting properties coming from model categories

Fibrations and cofibrations.

Let Top be the category of topological spaces, and let $C_{0}$ be the class of maps $S^{n}\to D^{n+1}$ , embeddings of the boundary $S^{n}=\partial D^{n+1}$ of a ball into the ball $D^{n+1}$ . Let $WC_{0}$ be the class of maps embedding the upper semi-sphere into the disk. $WC_{0}^{\perp \ell },WC_{0}^{\perp \ell r},C_{0}^{\perp \ell },C_{0}^{\perp \ell r}$ are the classes of fibrations, acyclic cofibrations, acyclic fibrations, and cofibrations.^[1]

Let sSet be the category of simplicial sets. Let $C_{0}$ be the class of boundary inclusions $\partial \Delta [n]\to \Delta [n]$ , and let $WC_{0}$ be the class of horn inclusions $\Lambda ^{i}[n]\to \Delta [n]$ . Then the classes of fibrations, acyclic cofibrations, acyclic fibrations, and cofibrations are, respectively, $WC_{0}^{\perp \ell },WC_{0}^{\perp \ell r},C_{0}^{\perp \ell },C_{0}^{\perp \ell r}$ .^[2]

Let Ch(R) be the category of chain complexes over a commutative ring R. Let $C_{0}$ be the class of maps of form

\cdots \to 0\to R\to 0\to 0\to \cdots \to \cdots \to R{\xrightarrow {\operatorname {id} }}R\to 0\to 0\to \cdots ,

and

WC_{0}

be

\cdots \to 0\to 0\to 0\to 0\to \cdots \to \cdots \to R{\xrightarrow {\operatorname {id} }}R\to 0\to 0\to \cdots .

Then

WC_{0}^{\perp \ell },WC_{0}^{\perp \ell r},C_{0}^{\perp \ell },C_{0}^{\perp \ell r}

are the classes of fibrations, acyclic cofibrations, acyclic fibrations, and cofibrations.^[3]

Elementary examples in various categories

In Set,

$\{\emptyset \to \{*\}\}^{\perp r}$ is the class of surjections,

$(\{a,b\}\to \{*\})^{\perp r}=(\{a,b\}\to \{*\})^{\perp \ell }$ is the class of injections.

In the category R-Mod of modules over a commutative ring R,

$\{0\to R\}^{\perp r},\{R\to 0\}^{\perp r}$ is the class of surjections, resp. injections,

A module M is projective, resp. injective, iff $0\to M$ is in $\{0\to R\}^{\perp \ell r}$ , resp. $M\to 0$ is in $\{R\to 0\}^{\perp rr}$ .

In the category Grp of groups,

$\{\mathbb {Z} \to 0\}^{\perp r}$ , resp. $\{0\to \mathbb {Z} \}^{\perp r}$ , is the class of injections, resp. surjections (where $\mathbb {Z}$ denotes the infinite cyclic group),

A group F is a free group iff $0\to F$ is in $\{0\to \mathbb {Z} \}^{\perp r\ell },$

A group A is torsion-free iff $0\to A$ is in $\{n\mathbb {Z} \to \mathbb {Z} :n>0\}^{\perp r},$

A subgroup A of B is pure iff $A\to B$ is in $\{n\mathbb {Z} \to \mathbb {Z} :n>0\}^{\perp r}.$

For a finite group G,

$\{0\to {\mathbb {Z} }/p{\mathbb {Z} }\}\perp G\to 1$ iff the order of G is prime to p,

$G\to 1\in (0\to {\mathbb {Z} }/p{\mathbb {Z} })^{\perp rr}$ iff G is a p-group,

H is nilpotent iff the diagonal map $H\to H\times H$ is in $(1\to *)^{\perp \ell r}$ where $(1\to *)$ denotes the class of maps $\{1\to G:G{\text{ arbitrary}}\},$

a finite group H is soluble iff $1\to H$ is in $\{0\to A:A{\text{ abelian}}\}^{\perp \ell r}=\{[G,G]\to G:G{\text{ arbitrary }}\}^{\perp \ell r}.$

In the category Top of topological spaces, let $\{0,1\}$ , resp. $\{0\leftrightarrow 1\}$ denote the discrete, resp. antidiscrete space with two points 0 and 1. Let $\{0\to 1\}$ denote the Sierpinski space of two points where the point 0 is open and the point 1 is closed, and let $\{0\}\to \{0\to 1\},\{1\}\to \{0\to 1\}$ etc. denote the obvious embeddings.

a space X satisfies the separation axiom T₀ iff $X\to \{*\}$ is in $(\{0\leftrightarrow 1\}\to \{*\})^{\perp r},$

a space X satisfies the separation axiom T₁ iff $\emptyset \to X$ is in $(\{0\to 1\}\to \{*\})^{\perp r},$

$(\{1\}\to \{0\to 1\})^{\perp \ell }$ is the class of maps with dense image,

$(\{0\to 1\}\to \{*\})^{\perp \ell }$ is the class of maps $f:X\to Y$ such that the topology on A is the pullback of topology on B, i.e. the topology on A is the topology with least number of open sets such that the map is continuous,

$(\emptyset \to \{*\})^{\perp r}$ is the class of surjective maps,

$(\emptyset \to \{*\})^{\perp r\ell }$ is the class of maps of form $A\to A\cup D$ where D is discrete,

$(\emptyset \to \{*\})^{\perp r\ell \ell }=(\{a\}\to \{a,b\})^{\perp \ell }$ is the class of maps $A\to B$ such that each connected component of B intersects $\operatorname {Im} A$ ,

$(\{0,1\}\to \{*\})^{\perp r}$ is the class of injective maps,

$(\{0,1\}\to \{*\})^{\perp \ell }$ is the class of maps $f:X\to Y$ such that the preimage of a connected closed open subset of Y is a connected closed open subset of X, e.g. X is connected iff $X\to \{*\}$ is in $(\{0,1\}\to \{*\})^{\perp \ell }$ ,

for a connected space X, each continuous function on X is bounded iff $\emptyset \to X\perp \cup _{n}(-n,n)\to \mathbb {R}$ where $\cup _{n}(-n,n)\to \mathbb {R}$ is the map from the disjoint union of open intervals $(-n,n)$ into the real line $\mathbb {R} ,$

a space X is Hausdorff iff for any injective map $\{a,b\}\hookrightarrow X$ , it holds $\{a,b\}\hookrightarrow X\perp \{a\to x\leftarrow b\}\to \{*\}$ where $\{a\leftarrow x\to b\}$ denotes the three-point space with two open points a and b, and a closed point x,

a space X is perfectly normal iff $\emptyset \to X\perp [0,1]\to \{0\leftarrow x\to 1\}$ where the open interval $(0,1)$ goes to x, and $0$ maps to the point $0$ , and $1$ maps to the point $1$ , and $\{0\leftarrow x\to 1\}$ denotes the three-point space with two closed points $0,1$ and one open point x.

In the category of metric spaces with uniformly continuous maps.

A space X is complete iff $\{1/n\}_{n\in \mathbb {N} }\to \{0\}\cup \{1/n\}_{n\in \mathbb {N} }\perp X\to \{0\}$ where $\{1/n\}_{n\in \mathbb {N} }\to \{0\}\cup \{1/n\}_{n\in \mathbb {N} }$ is the obvious inclusion between the two subspaces of the real line with induced metric, and $\{0\}$ is the metric space consisting of a single point,