Compound of dodecahedron and icosahedron
| First stellation of icosidodecahedron | |
|---|---|

| |
| Type | Dual compound |
| Coxeter diagram | |
| Stellation core | icosidodecahedron |
| Convex hull | Rhombic triacontahedron |
| Index | W47 |
| Polyhedra | 1 icosahedron 1 dodecahedron |
| Faces | 20 triangles 12 pentagons |
| Edges | 60 |
| Vertices | 32 |
| Symmetry group | icosahedral (Ih) |
In geometry, this polyhedron can be seen as either a polyhedral stellation or a compound.
As a compound
It can be seen as the compound of an icosahedron and dodecahedron. It is one of four compounds constructed from a Platonic solid or Kepler-Poinsot solid, and its dual.
It has icosahedral symmetry (Ih) and the same vertex arrangement as a rhombic triacontahedron.
This can be seen as the three-dimensional equivalent of the compound of two pentagons ({10/2} "decagram"); this series continues into the fourth dimension as the compound of 120-cell and 600-cell and into higher dimensions as compounds of hyperbolic tilings.
|
The intersection of both solids is the icosidodecahedron, and their convex hull is the rhombic triacontahedron. |
The decagon on the right is the Petrie polygon of both solids.
As a stellation
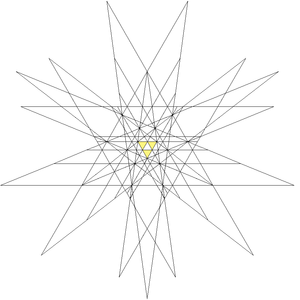
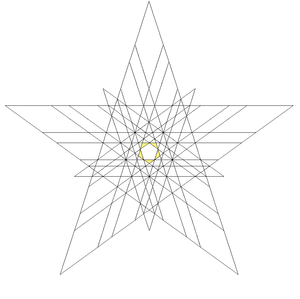
This polyhedron is the first stellation of the icosidodecahedron, and given as Wenninger model index 47.
The stellation facets for construction are:
In popular culture
In the film Tron (1982), the character Bit took this shape when not speaking.
In the cartoon series Steven Universe (2013-2019), Pink Steven's shield bubble, briefly used in the episode Change Your Mind, had this shape.
See also
- Compound of two tetrahedra
- Compound of cube and octahedron
- Compound of small stellated dodecahedron and great dodecahedron
- Compound of great stellated dodecahedron and great icosahedron
References
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.