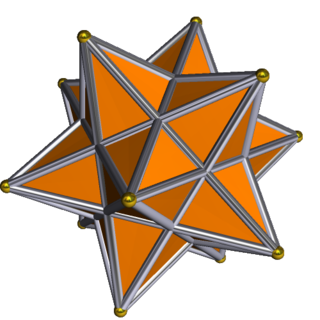
Great complex icosidodecahedron

Great complex icosidodecahedron
Type	Uniform star polyhedron
Elements	F = 32, E = 60 (30x2) V = 12 (χ = -16)
Faces by sides	20{3}+12{5/2}
Coxeter diagram
Wythoff symbol	5 | 3 5/3
Symmetry group	Ih, [5,3], *532
Index references	U-, C-, W-
Dual polyhedron	Great complex icosidodecacron
Vertex figure	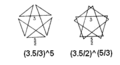(3.5/3)5 (3.5/2)5/3
Bowers acronym	Gacid

In geometry, the great complex icosidodecahedron is a degenerate uniform star polyhedron. It has 12 vertices, and 60 (doubled) edges, and 32 faces, 12 pentagrams and 20 triangles. All edges are doubled (making it degenerate), sharing 4 faces, but are considered as two overlapping edges as topological polyhedron.

It can be constructed from a number of different vertex figures.

As a compound

The great complex icosidodecahedron can be considered a compound of the small stellated dodecahedron, {5/2,5}, and great icosahedron, {3,5/2}, sharing the same vertices and edges, while the second is hidden, being completely contained inside the first.

Its two-dimensional analogue would be the compound of a regular pentagon, {5}, and regular pentagram, {5/2}. These shapes would share vertices, similarly to how its 3D equivalent shares edges.

Compound polyhedron Small stellated dodecahedron Great icosahedron Compound Compound polygon Pentagon Pentagram Compound

See also

• Small complex icosidodecahedron
• Small complex rhombicosidodecahedron
• Complex rhombidodecadodecahedron
• Great complex rhombicosidodecahedron

References

• Coxeter, Harold Scott MacDonald; Longuet-Higgins, M. S.; Miller, J. C. P. (1954), "Uniform polyhedra", Philosophical Transactions of the Royal Society of London. Series A. Mathematical and Physical Sciences, 246 (916): 401–450, doi:10.1098/rsta.1954.0003, ISSN 0080-4614, JSTOR 91532, MR 0062446, S2CID 202575183 (Table 6, degenerate cases)
• Weisstein, Eric W. "Great complex icosidodecahedron". MathWorld.
• Klitzing, Richard. "3D uniform polyhedra o5/3x3o5*a and o3/2x5/2o5*a - gacid".