Andrásfai graph

Andrásfai graph
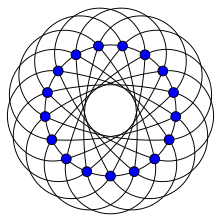Named after	Béla Andrásfai
Vertices	$3n-1$
Edges	${\frac {n(3n-1)}{2}}$
Diameter	2
Properties	Triangle-free Circulant
Notation	And(n)
Table of graphs and parameters

Two drawings of the And(4) graph

In graph theory, an Andrásfai graph is a triangle-free, circulant graph named after Béla Andrásfai.

Properties

The Andrásfai graph And(n) for any natural number n ≥ 1 is a circulant graph on 3n – 1 vertices, in which vertex k is connected by an edge to vertices k ± j, for every j that is congruent to 1 mod 3. For instance, the Wagner graph is an Andrásfai graph, the graph And(3).

The graph family is triangle-free, and And(n) has an independence number of n. From this the formula R(3,n) ≥ 3(n – 1) results, where R(n,k) is the Ramsey number. The equality holds for n = 3 and n = 4 only.

References

• Godsil, Chris; Royle, Gordon F. (2013) [2001]. "§6.10–6.12: The Andrásfai Graphs—Andrásfai Coloring Graphs, A Characterization". Algebraic Graph Theory. Graduate Texts in Mathematics. Vol. 207. Springer. pp. 118–123. ISBN 978-1-4613-0163-9.
• Andrásfai, Béla (1971). Ismerkedés a gráfelmélettel (in Hungarian). Budapest: Tankönyvkiadó. pp. 132–5. OCLC 908973331.
• Weisstein, Eric W. "Andrásfai Graph". MathWorld.

Related Items

• Petersen graph
• Cayley graph