Brent's method
In numerical analysis, Brent's method is a hybrid root-finding algorithm combining the bisection method, the secant method and inverse quadratic interpolation. It has the reliability of bisection but it can be as quick as some of the less-reliable methods. The algorithm tries to use the potentially fast-converging secant method or inverse quadratic interpolation if possible, but it falls back to the more robust bisection method if necessary. Brent's method is due to Richard Brent[1] and builds on an earlier algorithm by Theodorus Dekker.[2] Consequently, the method is also known as the Brent–Dekker method.
Modern improvements on Brent's method include Chandrupatla's method, which is simpler and faster for functions that are flat around their roots;[3][4] Ridders' method, which performs exponential interpolations instead of quadratic providing a simpler closed formula for the iterations; and the ITP method which is a hybrid between regula-falsi and bisection that achieves optimal worst-case and asymptotic guarantees.
Dekker's method[edit]
The idea to combine the bisection method with the secant method goes back to Dekker (1969).
Suppose that we want to solve the equation f(x) = 0. As with the bisection method, we need to initialize Dekker's method with two points, say a0 and b0, such that f(a0) and f(b0) have opposite signs. If f is continuous on [a0, b0], the intermediate value theorem guarantees the existence of a solution between a0 and b0.
Three points are involved in every iteration:
- bk is the current iterate, i.e., the current guess for the root of f.
- ak is the "contrapoint," i.e., a point such that f(ak) and f(bk) have opposite signs, so the interval [ak, bk] contains the solution. Furthermore, |f(bk)| should be less than or equal to |f(ak)|, so that bk is a better guess for the unknown solution than ak.
- bk−1 is the previous iterate (for the first iteration, we set bk−1 = a0).
Two provisional values for the next iterate are computed. The first one is given by linear interpolation, also known as the secant method:
and the second one is given by the bisection method
If the result of the secant method, s, lies strictly between bk and m, then it becomes the next iterate (bk+1 = s), otherwise the midpoint is used (bk+1 = m).
Then, the value of the new contrapoint is chosen such that f(ak+1) and f(bk+1) have opposite signs. If f(ak) and f(bk+1) have opposite signs, then the contrapoint remains the same: ak+1 = ak. Otherwise, f(bk+1) and f(bk) have opposite signs, so the new contrapoint becomes ak+1 = bk.
Finally, if |f(ak+1)| < |f(bk+1)|, then ak+1 is probably a better guess for the solution than bk+1, and hence the values of ak+1 and bk+1 are exchanged.
This ends the description of a single iteration of Dekker's method.
Dekker's method performs well if the function f is reasonably well-behaved. However, there are circumstances in which every iteration employs the secant method, but the iterates bk converge very slowly (in particular, |bk − bk−1| may be arbitrarily small). Dekker's method requires far more iterations than the bisection method in this case.
Brent's method[edit]
Brent (1973) proposed a small modification to avoid the problem with Dekker's method. He inserts an additional test which must be satisfied before the result of the secant method is accepted as the next iterate. Two inequalities must be simultaneously satisfied:
Given a specific numerical tolerance , if the previous step used the bisection method, the inequality must hold to perform interpolation, otherwise the bisection method is performed and its result used for the next iteration.
If the previous step performed interpolation, then the inequality is used instead to perform the next action (to choose) interpolation (when inequality is true) or bisection method (when inequality is not true).
Also, if the previous step used the bisection method, the inequality must hold, otherwise the bisection method is performed and its result used for the next iteration. If the previous step performed interpolation, then the inequality is used instead.
This modification ensures that at the kth iteration, a bisection step will be performed in at most additional iterations, because the above conditions force consecutive interpolation step sizes to halve every two iterations, and after at most iterations, the step size will be smaller than , which invokes a bisection step. Brent proved that his method requires at most N2 iterations, where N denotes the number of iterations for the bisection method. If the function f is well-behaved, then Brent's method will usually proceed by either inverse quadratic or linear interpolation, in which case it will converge superlinearly.
Furthermore, Brent's method uses inverse quadratic interpolation instead of linear interpolation (as used by the secant method). If f(bk), f(ak) and f(bk−1) are distinct, it slightly increases the efficiency. As a consequence, the condition for accepting s (the value proposed by either linear interpolation or inverse quadratic interpolation) has to be changed: s has to lie between (3ak + bk) / 4 and bk.
Algorithm[edit]
This section possibly contains original research. (February 2019) |
input a, b, and (a pointer to) a function for f
calculate f(a)
calculate f(b)
if f(a)f(b) ≥ 0 then
exit function because the root is not bracketed.
end if
if |f(a)| < |f(b)| then
swap (a,b)
end if
c := a
set mflag
repeat until f(b or s) = 0 or |b − a| is small enough (convergence)
if f(a) ≠ f(c) and f(b) ≠ f(c) then
(inverse quadratic interpolation)
else
(secant method)
end if
if (condition 1) s is not between and b or
(condition 2) (mflag is set and |s−b| ≥ |b−c|/2) or
(condition 3) (mflag is cleared and |s−b| ≥ |c−d|/2) or
(condition 4) (mflag is set and |b−c| < |δ|) or
(condition 5) (mflag is cleared and |c−d| < |δ|) then
(bisection method)
set mflag
else
clear mflag
end if
calculate f(s)
d := c (d is assigned for the first time here; it won't be used above on the first iteration because mflag is set)
c := b
if f(a)f(s) < 0 then
b := s
else
a := s
end if
if |f(a)| < |f(b)| then
swap (a,b)
end if
end repeat
output b or s (return the root)
Example[edit]
Suppose that we are seeking a zero of the function defined by f(x) = (x + 3)(x − 1)2.
We take [a0, b0] = [−4, 4/3] as our initial interval.
We have f(a0) = −25 and f(b0) = 0.48148 (all numbers in this section are rounded), so the conditions f(a0) f(b0) < 0 and |f(b0)| ≤ |f(a0)| are satisfied.
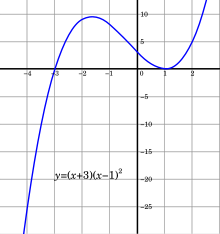
- In the first iteration, we use linear interpolation between (b−1, f(b−1)) = (a0, f(a0)) = (−4, −25) and (b0, f(b0)) = (1.33333, 0.48148), which yields s = 1.23256. This lies between (3a0 + b0) / 4 and b0, so this value is accepted. Furthermore, f(1.23256) = 0.22891, so we set a1 = a0 and b1 = s = 1.23256.
- In the second iteration, we use inverse quadratic interpolation between (a1, f(a1)) = (−4, −25) and (b0, f(b0)) = (1.33333, 0.48148) and (b1, f(b1)) = (1.23256, 0.22891). This yields 1.14205, which lies between (3a1 + b1) / 4 and b1. Furthermore, the inequality |1.14205 − b1| ≤ |b0 − b−1| / 2 is satisfied, so this value is accepted. Furthermore, f(1.14205) = 0.083582, so we set a2 = a1 and b2 = 1.14205.
- In the third iteration, we use inverse quadratic interpolation between (a2, f(a2)) = (−4, −25) and (b1, f(b1)) = (1.23256, 0.22891) and (b2, f(b2)) = (1.14205, 0.083582). This yields 1.09032, which lies between (3a2 + b2) / 4 and b2. But here Brent's additional condition kicks in: the inequality |1.09032 − b2| ≤ |b1 − b0| / 2 is not satisfied, so this value is rejected. Instead, the midpoint m = −1.42897 of the interval [a2, b2] is computed. We have f(m) = 9.26891, so we set a3 = a2 and b3 = −1.42897.
- In the fourth iteration, we use inverse quadratic interpolation between (a3, f(a3)) = (−4, −25) and (b2, f(b2)) = (1.14205, 0.083582) and (b3, f(b3)) = (−1.42897, 9.26891). This yields 1.15448, which is not in the interval between (3a3 + b3) / 4 and b3). Hence, it is replaced by the midpoint m = −2.71449. We have f(m) = 3.93934, so we set a4 = a3 and b4 = −2.71449.
- In the fifth iteration, inverse quadratic interpolation yields −3.45500, which lies in the required interval. However, the previous iteration was a bisection step, so the inequality |−3.45500 − b4| ≤ |b4 − b3| / 2 need to be satisfied. This inequality is false, so we use the midpoint m = −3.35724. We have f(m) = −6.78239, so m becomes the new contrapoint (a5 = −3.35724) and the iterate remains the same (b5 = b4).
- In the sixth iteration, we cannot use inverse quadratic interpolation because b5 = b4. Hence, we use linear interpolation between (a5, f(a5)) = (−3.35724, −6.78239) and (b5, f(b5)) = (−2.71449, 3.93934). The result is s = −2.95064, which satisfies all the conditions. But since the iterate did not change in the previous step, we reject this result and fall back to bisection. We update s = -3.03587, and f(s) = -0.58418.
- In the seventh iteration, we can again use inverse quadratic interpolation. The result is s = −3.00219, which satisfies all the conditions. Now, f(s) = −0.03515, so we set a7 = b6 and b7 = −3.00219 (a7 and b7 are exchanged so that the condition |f(b7)| ≤ |f(a7)| is satisfied). (Correct : linear interpolation )
- In the eighth iteration, we cannot use inverse quadratic interpolation because a7 = b6. Linear interpolation yields s = −2.99994, which is accepted. (Correct : )
- In the following iterations, the root x = −3 is approached rapidly: b9 = −3 + 6·10−8 and b10 = −3 − 3·10−15. (Correct : Iter 9 : f(s) = −1.4 × 10−7, Iter 10 : f(s) = 6.96 × 10−12)
Implementations[edit]
- Brent (1973) published an Algol 60 implementation.
- Netlib contains a Fortran translation of this implementation with slight modifications.
- The PARI/GP method
solveimplements the method. - Other implementations of the algorithm (in C++, C, and Fortran) can be found in the Numerical Recipes books.
- The Apache Commons Math library implements the algorithm in Java.
- The SciPy optimize module implements the algorithm in Python (programming language)
- The Modelica Standard Library implements the algorithm in Modelica.
- The
unirootfunction implements the algorithm in R (software). - The
fzerofunction implements the algorithm in MATLAB. - The Boost (C++ libraries) implements two algorithms based on Brent's method in C++ in the Math toolkit:
- Function minimization at minima.hpp with an example locating function minima.
- Root finding implements the newer TOMS748, a more modern and efficient algorithm than Brent's original, at TOMS748, and Boost.Math rooting finding that uses TOMS748 internally with examples.
- The Optim.jl package implements the algorithm in Julia (programming language)
- The SICMUtils computer algebra system (written in Clojure (programming language)) implements a variant of the algorithm designed for univariate function minimization.
- Root-Finding in C# library hosted in Code Project.
References[edit]
- ^ Brent 1973
- ^ Dekker 1969
- ^ Chandrupatla, Tirupathi R. (1997). "A new hybrid quadratic/Bisection algorithm for finding the zero of a nonlinear function without using derivatives". Advances in Engineering Software. 28 (3): 145–149. doi:10.1016/S0965-9978(96)00051-8.
- ^ "Ten Little Algorithms, Part 5: Quadratic Extremum Interpolation and Chandrupatla's Method - Jason Sachs".
- Brent, R. P. (1973), "Chapter 4: An Algorithm with Guaranteed Convergence for Finding a Zero of a Function", Algorithms for Minimization without Derivatives, Englewood Cliffs, NJ: Prentice-Hall, ISBN 0-13-022335-2
- Dekker, T. J. (1969), "Finding a zero by means of successive linear interpolation", in Dejon, B.; Henrici, P. (eds.), Constructive Aspects of the Fundamental Theorem of Algebra, London: Wiley-Interscience, ISBN 978-0-471-20300-1
Further reading[edit]
- Atkinson, Kendall E. (1989). "Section 2.8.". An Introduction to Numerical Analysis (2nd ed.). John Wiley and Sons. ISBN 0-471-50023-2.
- Press, W. H.; Teukolsky, S. A.; Vetterling, W. T.; Flannery, B. P. (2007). "Section 9.3. Van Wijngaarden–Dekker–Brent Method". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. Archived from the original on 2011-08-11. Retrieved 2012-02-28.
- Alefeld, G. E.; Potra, F. A.; Shi, Yixun (September 1995). "Algorithm 748: Enclosing Zeros of Continuous Functions". ACM Transactions on Mathematical Software. 21 (3): 327–344. doi:10.1145/210089.210111. S2CID 207192624.
External links[edit]
- zeroin.f at Netlib.
- module brent in C++ (also C, Fortran, Matlab) Archived 2018-04-05 at the Wayback Machine by John Burkardt
- GSL implementation.
- Boost C++ implementation.
- Python (Scipy) implementation














