Computer-generated holography
Computer-generated holography (CGH) is a technique that uses computer algorithms to generate holograms. It involves generating holographic interference patterns. A computer-generated hologram can be displayed on a dynamic holographic display, or it can be printed onto a mask or film using lithography.[1] When a hologram is printed onto a mask or film, it is then illuminated by a coherent light source to display the holographic images.
The term "computer-generated holography" has become used to denote the whole process chain of synthetically preparing holographic light wavefronts suitable for observation.[2][3] If holographic data of existing objects is generated optically and recorded and processed digitally, and subsequently displayed, this is termed CGH as well.
Compared to classical holograms, computer-generated holograms have the advantage that the objects that one wants to show do not have to possess any physical reality, and can be completely synthetically generated.
Ultimately, computer-generated holography might expand upon all the roles of current computer-generated imagery. Holographic computer displays might be used for a wide range of applications, for example computer-aided design (CAD), gaming, and holographic video.
Overview
[edit]Holography is a technique originally invented by Hungarian physicist Dennis Gabor (1900–1979) to improve the resolving power on electron microscopes. An object is illuminated with a coherent (usually monochromatic) light beam; the scattered light is brought to interference with a reference beam of the same source, recording the interference pattern. CGH as defined in the introduction has broadly three tasks:
- Computation of the virtual scattered wavefront
- Encoding the wavefront data, preparing it for display
- Reconstruction: Modulating the interference pattern onto a coherent light beam by technological means, to transport it to the user observing the hologram.
Note that it is not always justified to make a strict distinction between these steps; however it helps the discussion to structure it in this way.
Wavefront computation
[edit]Computer generated holograms offer important advantages over optical holograms since there is no need for a real object. Because of this breakthrough, a three-dimensional display was expected when the first algorithms were reported at 1966.[4]
Unfortunately, the researchers soon realized that there are noticeable lower and upper bounds in terms of computational speed and image quality and fidelity respectively. Wavefront calculations are computationally very intensive; even with modern mathematical techniques and high-end computing equipment, real-time computation is tricky. There are many different methods for calculating the interference pattern for a CGH. In the following 25 years, many methods for computer-generated holograms were proposed in the fields of holographic information and computational reduction as well as in computational and quantization techniques.[5][6][7][8][9][10][11] The algorithms can be categorized in two main concepts: Fourier transform holograms and point source holograms.
One of the more prevalent methods that can be used to generate phase-only holograms is the Gerchberg-Saxton (GS) algorithm.[12][13]
Fourier transform method
[edit]In the first one, the Fourier transformation is used to simulate the propagation of each plane of depth of the object to the hologram plane. The Fourier transformation concept was first introduced by Byron R. Brown and Adolf W. Lohmann[4] with the detour phase method leading to cell oriented holograms. A coding technique suggested by Burch[14] replaced the cell oriented holograms by point holograms and made this kind of computer generated holograms more attractive. In a Fourier Transform hologram the reconstruction of the image occurs in the far field. This is usually achieved by using the Fourier transforming properties of a positive lens for reconstruction. So there are two steps in this process: computing the light field in the far observer plane, and then Fourier transforming this field back to the lens plane. These holograms are called Fourier Based Holograms. First CGHs based on the Fourier transform could reconstruct only 2D images. Brown and Lohmann[15] introduced a technique to calculate computer generated holograms of 3D objects. Calculation of the light propagation from three-dimensional objects is performed according to the usual parabolic approximation to the Fresnel-Kirchhoff diffraction integral. The wavefront to be reconstructed by the hologram is, therefore, the superposition of the Fourier transforms of each object plane in depth, modified by a quadratic phase factor.
Point source holograms
[edit]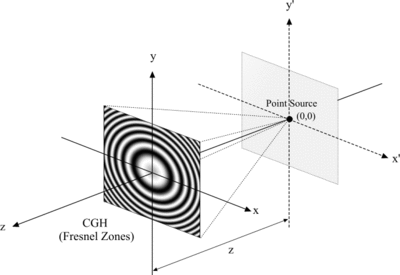
The second computational strategy is based on the point source concept, where the object is broken down in self-luminous points. An elementary hologram is calculated for every point source and the final hologram is synthesized by superimposing all the elementary holograms. This concept has been first reported by Waters[16] whose major assumption originated with Rogers[17] who recognized that a Fresnel zone plate could be considered a special case of the hologram proposed by Gabor. But, as far as most of the object points were non-zero, the computational complexity of the point-source concept was much higher than in the Fourier transformation concept. Some researchers tried to overcome this drawback by predefining and storing all the possible elementary holograms using special data storage techniques[18] because of the huge capacity that is needed in this case, others by using special hardware.[19]
In the point-source concept the major problem is the trade-off between data storage capacity and computational speed. In particular, algorithms that increase computational speed usually have much greater data storage requirements[18] while algorithms that reduce data storage requirements have high computational complexity[20][21][22] (though some optimizations are possible[23]).
Another concept which leads to point source CGHs is the ray tracing method. Ray tracing is perhaps the simplest method of computer generated holography to visualize. Essentially, the path length difference between the distance a virtual "reference beam" and a virtual "object beam" have to travel is calculated; this will give the relative phase of the scattered object beam.
Over the last three decades, both concepts have made remarkable progress improving computational speed and image quality. However, some technical restraints, like computation and storage capacity, still burden digital holography which makes real-time applications almost impossible with current standard computer hardware.
Generated Holography
[edit]Once it is known what the scattered wavefront of the object looks like or how it may be computed, it must be fixed on a spatial light modulator (SLM), abusing this term to include not only LCD displays or similar devices, but also films and masks. Basically, there are different types of SLMs available: Pure phase modulators (retarding the illuminating wave), pure amplitude modulators (blocking the illumination light), polarization modulators (influencing the polarization state of light)[24] and SLMs which have the capability of combined phase/amplitude modulation.[25]
In the case of pure phase or amplitude modulation, clearly quality losses are unavoidable. Early forms of pure amplitude holograms were simply printed in black and white, meaning that the amplitude had to be encoded with one bit of depth only.[4] Similarly, the kinoform is a pure-phase encoding invented at IBM in the early days of CGH.[26]
Even if a fully complex phase/amplitude modulation would be ideal, a pure phase or pure amplitude solution is normally preferred because it is much easier to implement technologically. Nevertheless, for the creation of complicated light distribution simultaneous modulation of amplitude and phase is reasonable. So far two different approaches for amplitude-phase-modulation have been implemented. One is based on phase-only or amplitude-only modulation and consecutive spatial filtering,[27] the other one is based on polarization holograms with variable orientation and magnitude of local birefringence.[28] Holograms with a constraint, such as phase-only or amplitude-only, may be computed via algorithms such as the Gerchberg-Saxton algorithm or more general optimisation algorithms such as direct search, simulated annealing [29] or stochastic gradient descent using, for example, TensorFlow.[30]
Reconstruction
[edit]The third (technical) issue is beam modulation and actual wavefront reconstruction. Masks may be printed, resulting often in a grained pattern structure since most printers can make only dots (although very small ones). Films may be developed by laser exposure. Holographic displays are currently yet a challenge (as of 2008[update]), although successful prototypes have been built. An ideal display for computer generated holograms would consist of pixels smaller than a wavelength of light with adjustable phase and brightness. Such displays have been called phased array optics.[31] Further progress in nanotechnology is required to build them.
Applications
[edit]Currently, several companies and university departments are researching on the field of CGH devices:
- VividQ[32] provides software for real-time CGH devices, allowing for the generation of images with over 200 depth layers using standard computing power
- MIT Media Lab[33] has developed the "Holovideo" CGH display
- SeeReal Technologies have prototyped a CGH display
- Cortical Cafe CGH Kit[34] is a CGH related hobbyist site with instructions, source code, and a web-application for CGH creation.
In electron optics
[edit]Recently computer-generated holography has been extended in its usage beyond light optics, and applied in generating structured electron wavefunctions with a desired amplitude and phase profile. The computer generated holograms are designed by the interference of a target wave with a reference wave, which could be, e.g. a plane-like wave slightly tilted in one direction. The holographic diffractive optical elements used are usually constructed out of thin membranes of materials such as silicon nitride.
References
[edit]- ^ Sahin, Erdem; Stoykova, Elena; Mäkinen, Jani; Gotchev, Atanas (2020-03-20). "Computer-Generated Holograms for 3D Imaging: A Survey" (PDF). ACM Computing Surveys. 53 (2): 32:1–32:35. doi:10.1145/3378444. ISSN 0360-0300. S2CID 215854874.
- ^ Ch. Slinger; C. Cameron; M. Stanley (Aug 2005), "Computer-Generated Holography as a Generic Display Technology", Computer, 38 (8): 46–53, doi:10.1109/mc.2005.260, S2CID 7394380
- ^ Yaraş, Fahri; Kang, Hoonjong; Onural, Levent (29 September 2009). "Real-time phase-only color holographic video display system using LED illumination". Applied Optics. 48 (34): H48-53. Bibcode:2009ApOpt..48H..48Y. doi:10.1364/AO.48.000H48. hdl:11693/22545. PMID 19956301. S2CID 5890199.
- ^ a b c Brown, Byron R.; Lohmann, Adolf W. (1966). "Complex spatial filtering with binary masks". Applied Optics. 5 (6): 967–9. Bibcode:1966ApOpt...5..967B. doi:10.1364/AO.5.000967. PMID 20048989.
- ^ L.B. Lesem; P.M. Hirsch & J.A. Jordan (1968). "Computer synthesis of holograms for 3-D display". Communications of the ACM. 11 (10): 661–674. doi:10.1145/364096.364111. S2CID 18707299.
- ^ L.B. Lesem; P.M. Hirsch & J.A. Jordan (1969). "The Kinοform: A New Wavefront Reconstruction Device" (PDF). IBM Journal of Research and Development. 13 (2): 150–155. doi:10.1147/rd.132.0150.
- ^ W.H. Lee (1970). "Sampled Fourier Transform Hologram Generated by Computer". Appl. Opt. 9 (3): 639–643. doi:10.1364/AO.9.000639. PMID 20076253. S2CID 15902468.
- ^ D. Leseberg & O. Bryngdahl (1984). "Computer-generated rainbow holograms". Appl. Opt. 23 (14): 2441–2447. Bibcode:1984ApOpt..23.2441L. doi:10.1364/AO.23.002441. PMID 18213016.
- ^ F. Wyrowski; R. Hauck & O. Bryngdahl (1987). "Computer-generated holography: hologram repetition and phase manipulation". J. Opt. Soc. Am. A. 4 (4): 694–698. Bibcode:1987JOSAA...4..694W. doi:10.1364/JOSAA.4.000694.
- ^ D. Leseberg & C. Frère (1988). "Computer-generated holograms of 3-D objects composed of tilted planar segments". Appl. Opt. 27 (14): 3020–3024. Bibcode:1988ApOpt..27.3020L. doi:10.1364/AO.27.003020. PMID 20531880.
- ^ Clark, Matthew (1 September 1999). "Two-dimensional, three-dimensional, and gray-scale images reconstructed from computer-generated holograms designed by use of a direct-search method". Applied Optics. 38 (25): 5331–5337. Bibcode:1999ApOpt..38.5331C. doi:10.1364/ao.38.005331. PMID 18324035.
- ^ Memmolo, Pasquale; Miccio, Lisa; Merola, Francesco; Paciello, Antonio; Embrione, Valerio; Fusco, Sabato; Ferraro, Pietro; Antonio Netti, Paolo (2014-01-01). "Investigation on specific solutions of Gerchberg–Saxton algorithm". Optics and Lasers in Engineering. 52: 206–211. Bibcode:2014OptLE..52..206M. doi:10.1016/j.optlaseng.2013.06.008. ISSN 0143-8166.
- ^ Liu, Shujian; Takaki, Yasuhiro (January 2020). "Optimization of Phase-Only Computer-Generated Holograms Based on the Gradient Descent Method". Applied Sciences. 10 (12): 4283. doi:10.3390/app10124283. ISSN 2076-3417.
- ^ J.J. Burch (1967). "A Computer Algorithm for the Synthesis of Spatial Frequency Filters". Proceedings of the IEEE. 55 (4): 599–601. doi:10.1109/PROC.1967.5620.
- ^ B.R. Brown & A.W. Lohmann (1969). "Computer-generated Binary Holograms" (PDF). IBM Journal of Research and Development. 13 (2): 160–168. doi:10.1147/rd.132.0160. Archived from the original (PDF) on 2012-02-24. Retrieved 2009-06-17.
- ^ J.P.Waters (1968). "Holographic Image synthesis utilizing theoretical methods". Appl. Phys. Lett. 9 (11): 405–407. doi:10.1063/1.1754630.
- ^ G.L. Rogers (1950). "Gabor diffraction microscopy: the hologram as a generalized zone-plate". Nature. 166 (4214): 237. Bibcode:1950Natur.166..237R. doi:10.1038/166237a0. PMID 15439257.
- ^ a b M. Lucente (1993). "Interactive computation of holograms using a look-up table". Journal of Electronic Imaging. 2: 28–34. Bibcode:1993JEI.....2...28L. CiteSeerX 10.1.1.51.4513. doi:10.1117/12.133376.
- ^ T. Ito; K. Yoshida; S. Takahashi; T. Yabe; et al. (1996). "Special-purpose computer for holography HORN-2". Comput. Phys. Commun. 93 (1): 13–20. Bibcode:1996CoPhC..93...13I. doi:10.1016/0010-4655(95)00125-5.
- ^ H. Yang; E. S. Kim (1996). "Waveform-decomposition-based algorithm for horizontal parallax-only-display computer-generated holograms". Opt. Lett. 21 (7): 510–512. Bibcode:1996OptL...21..510Y. doi:10.1364/OL.21.000510. PMID 19865455.
- ^ J. L. Juárez-Peréz; A. Olivares- Peréz & L. R. Berriel-Valdos (1997). "Nonredundant calculations for creating Fresnel holograms". Appl. Opt. 36 (29): 7437–7443. doi:10.1364/AO.36.007437. PMID 18264254.
- ^ H. Yoshikawa; S. Iwase & T. Oneda (2001). "Fast Computation of Fresnel Holograms employing Difference". Optical Review. 8 (5): 331–335. Bibcode:2001OptRv...8..331Y. doi:10.1007/s10043-001-0331-y.
- ^ A. D. Stein; Z. Wang; J. S. Leigh, Jr. (1992). "Computer-generated holograms: A simplified ray-tracing approach". Computers in Physics. 6 (4): 389–393. Bibcode:1992ComPh...6..389S. doi:10.1063/1.168429. Archived from the original on 2010-02-01. Retrieved 2010-09-14.
- ^ M. Nakajima; H. Komatsu; Y. Mitsuhashi; T. Morikawa (1976). "Computer generated polarization holograms: phase recording by polarization effect in photodichroic materials". Appl. Opt. 15 (4): 1030–1033. Bibcode:1976ApOpt..15.1030N. doi:10.1364/ao.15.001030. PMID 20165114.
- ^ W. Lauterborn; T. Kurz (2002). Coherent Optics (2nd ed.). Springer. ISBN 978-3-540-43933-2.
- ^ L. B. Lesem; P. M. Hirsch; J. A. Jordan, Jr. (1969). "The Kinoform: A New Wavefront Reconstruction Device". IBM Journal of Research and Development. 13 (2): 150–155. doi:10.1147/rd.132.0150.
- ^ V. Arrizon; G. Mendez; D. Sanchez-de-La-Llave (2005). "Accurate encoding of arbitrary complex fields with amplitude-only liquid crystal spatial light modulators". Opt. Express. 13 (20): 7913–7927. Bibcode:2005OExpr..13.7913A. doi:10.1364/opex.13.007913. PMID 19498821.
- ^ M. Fratz; P. Fischer; D. M. Giel (2009). "Full phase and amplitude control in computer-generated holography". Opt. Lett. 34 (23): 3659–3661. Bibcode:2009OptL...34.3659F. doi:10.1364/ol.34.003659. PMID 19953153. S2CID 5726900.
- ^ P. J. Christopher; A. Kadis; G. S. D. Gordon; T. D. Wilkinson (2022). "HoloGen: An open-source toolbox for high-speed hologram generation". Computer Physics Communications. 270 (108139): 108139. arXiv:2008.12214. Bibcode:2022CoPhC.27008139C. doi:10.1016/j.cpc.2021.108139. ISSN 0010-4655. S2CID 221340546.
- ^ G. S. D. Gordon (2020-04-21), gsdgordon/hologramGenerationTensorflow, retrieved 2024-01-20
- ^ Wowk B (1996). "Phased Array Optics". In BC Crandall (ed.). Molecular Speculations on Global Abundance. MIT Press. pp. 147–160. ISBN 978-0-262-03237-7. Retrieved 2007-02-18.
- ^ "VividQ Home". vivid-q.com.
- ^ "The Holovideo Page by Mark Lucente". mit.edu.
- ^ "CorticalCafe Free Desktop Software". corticalcafe.com.
- Ekberg M., Larsson M., Hård S. (1990). "Multilevel Phase Holograms Manufactured by Electron-Beam Lithography". Opt. Lett. (OSA) 15 (10): 568-569. 0146-9592/90/100568-02$2.00/0
