Conceptual graph

Conceptual graphs (CGs) are a formalism for knowledge representation. In the first published paper on CGs, John F. Sowa (Sowa 1976) used them to represent the conceptual schemas used in database systems. The first book on CGs (Sowa 1984) applied them to a wide range of topics in artificial intelligence, computer science, and cognitive science.

Since 1984, the model has been developed along three main directions.

A graphical interface for first-order logic

In this approach, a formula in first-order logic (predicate calculus) is represented by a labeled graph.

A linear notation, called the Conceptual Graph Interchange Format (CGIF), has been standardized in the ISO standard for common logic.

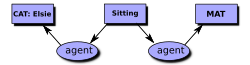
The diagram on the right is an example of the display form for a conceptual graph. Each box is called a concept node, and each oval is called a relation node. In CGIF, this CG would be represented by the following statement:

   [Cat Elsie] [Sitting *x] [Mat *y] (agent ?x Elsie) (location ?x ?y)

In CGIF, brackets enclose the information inside the concept nodes, and parentheses enclose the information inside the relation nodes. The letters x and y, which are called coreference labels, show how the concept and relation nodes are connected. In the Common Logic Interchange Format (CLIF), those letters are mapped to variables, as in the following statement:

   (exists ((x Sitting) (y Mat)) (and (Cat Elsie) (agent x Elsie) (location x y)))

As this example shows, the asterisks on the coreference labels *x and *y in CGIF map to existentially quantified variables in CLIF, and the question marks on ?x and ?y map to bound variables in CLIF. A universal quantifier, represented @every*z in CGIF, would be represented forall (z) in CLIF.

Reasoning can be done by translating graphs into logical formulas, then applying a logical inference engine.

Diagrammatic calculus of logics

Another research branch continues the work on existential graphs of Charles Sanders Peirce, which were one of the origins of conceptual graphs as proposed by Sowa. In this approach, developed in particular by Dau (Dau 2003), conceptual graphs are conceptual diagrams rather than graphs in the sense of graph theory, and reasoning operations are performed by operations on these diagrams.

Graph-based knowledge representation and reasoning model

Key features of GBKR, the graph-based knowledge representation and reasoning model developed by Chein and Mugnier and the Montpellier group (Chein & Mugnier 2009), can be summarized as follows:

all kinds of knowledge (ontology, rules, constraints and facts) are labeled graphs, which provide an intuitive and easily understandable means to represent knowledge,
reasoning mechanisms are based on graph notions, basically the classical notion of graph homomorphism; this allows, in particular, to link basic reasoning problems to other fundamental problems in computer science (problems concerning conjunctive queries in relational databases, constraint satisfaction problem, ...),
the formalism is logically founded, i.e., it has a semantics in first-order logic and the inference mechanisms are sound and complete with respect to deduction in first-order logic,
from a computational viewpoint, the graph homomorphism notion was recognized in the 90s as a central notion, and complexity results and efficient algorithms have been obtained in several domains.

COGITANT and COGUI are tools that implement the GBKR model. COGITANT is a library of C++ classes that implement most of the GBKR notions and reasoning mechanisms. COGUI is a graphical user interface dedicated to the construction of a GBKR knowledge base (it integrates COGITANT and, among numerous functionalities, it contains a translator from GBKR to RDF/S and conversely).

Sentence generalization and generalization diagrams

Sentence generalization and generalization diagrams can be defined as a special sort of conceptual graphs which can be constructed automatically from syntactic parse trees and support semantic classification task (Galitsky et al 2010). Similarity measure between syntactic parse trees can be done as a generalization operation on the lists of sub-trees of these trees. The diagrams are representation of mapping between the syntax generalization level and semantics generalization level (anti-unification of logic forms). Generalization diagrams are intended to be more accurate semantic representation than conventional conceptual graphs for individual sentences because only syntactic commonalities are represented at semantic level.

References

Chein, Michel; Mugnier, Marie-Laure (2009). Graph-based Knowledge Representation: Computational Foundations of Conceptual Graphs. Springer. ISBN 978-1-84800-285-2. {{cite book}}: Invalid |ref=harv (help)
Dau, F. (2003). "The Logic System of Concept Graphs with Negation and Its Relationship to Predicate Logic". Lecture Notes in Computer Science. 2892. Springer. {{cite journal}}: Invalid |ref=harv (help)
Sowa, John F. (July 1976). "Conceptual Graphs for a Data Base Interface" (PDF). IBM Journal of Research and Development. 20 (4): 336–357. doi:10.1147/rd.204.0336. {{cite journal}}: Invalid |ref=harv (help)
Sowa, John F. (1984). Conceptual Structures: Information Processing in Mind and Machine. Reading, MA: Addison-Wesley. ISBN 978-0-201-14472-7. {{cite book}}: Invalid |ref=harv (help)
Galitsky, Boris; Dobrocsi, Gabor; de la Rosa, Josep Lluis; Kuznetsov, Sergei O. (2010). "From Generalization of Syntactic Parse Trees to Conceptual Graphs". Lecture Notes in Computer Science. 6208. Springer. {{cite journal}}: Invalid |ref=harv (help)
Velardi, Paola; Pazienza, Maria Teresa; De' Giovanetti, Mario (March 1988). "Conceptual graphs for the analysis and generation of sentences". IBM Journal of Research and Development. 32 (2). IBM Corp. Riverton, NJ, USA: 251–267. doi:10.1147/rd.322.0251.

External links

Resources