Measure of relative information in probability theory
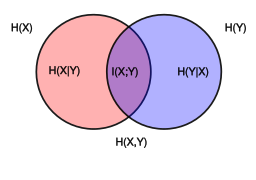
Venn diagram showing additive and subtractive relationships various information measures associated with correlated variables
X
{\displaystyle X}
Y
{\displaystyle Y}
joint entropy
H
(
X
,
Y
)
{\displaystyle \mathrm {H} (X,Y)}
individual entropy
H
(
X
)
{\displaystyle \mathrm {H} (X)}
H
(
X
|
Y
)
{\displaystyle \mathrm {H} (X|Y)}
H
(
Y
)
{\displaystyle \mathrm {H} (Y)}
H
(
Y
|
X
)
{\displaystyle \mathrm {H} (Y|X)}
mutual information
I
(
X
;
Y
)
{\displaystyle \operatorname {I} (X;Y)}
In information theory , the conditional entropy quantifies the amount of information needed to describe the outcome of a random variable
Y
{\displaystyle Y}
X
{\displaystyle X}
shannons , nats , or hartleys . The entropy of
Y
{\displaystyle Y}
X
{\displaystyle X}
is written as
H
(
Y
|
X
)
{\displaystyle \mathrm {H} (Y|X)}
The conditional entropy of
Y
{\displaystyle Y}
X
{\displaystyle X}
H
(
Y
|
X
)
=
−
∑
x
∈
X
,
y
∈
Y
p
(
x
,
y
)
log
p
(
x
,
y
)
p
(
x
)
{\displaystyle \mathrm {H} (Y|X)\ =-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log {\frac {p(x,y)}{p(x)}}}
(Eq.1 )
where
X
{\displaystyle {\mathcal {X}}}
Y
{\displaystyle {\mathcal {Y}}}
support sets of
X
{\displaystyle X}
Y
{\displaystyle Y}
Note: Here, the convention is that the expression
0
log
0
{\displaystyle 0\log 0}
lim
θ
→
0
+
θ
log
θ
=
0
{\displaystyle \lim _{\theta \to 0^{+}}\theta \,\log \theta =0}
[ 1]
Intuitively, notice that by definition of expected value and of conditional probability ,
H
(
Y
|
X
)
{\displaystyle \displaystyle H(Y|X)}
H
(
Y
|
X
)
=
E
[
f
(
X
,
Y
)
]
{\displaystyle H(Y|X)=\mathbb {E} [f(X,Y)]}
f
{\displaystyle f}
f
(
x
,
y
)
:=
−
log
(
p
(
x
,
y
)
p
(
x
)
)
=
−
log
(
p
(
y
|
x
)
)
{\displaystyle \displaystyle f(x,y):=-\log \left({\frac {p(x,y)}{p(x)}}\right)=-\log(p(y|x))}
f
{\displaystyle \displaystyle f}
(
x
,
y
)
{\displaystyle \displaystyle (x,y)}
(
Y
=
y
)
{\displaystyle \displaystyle (Y=y)}
(
X
=
x
)
{\displaystyle \displaystyle (X=x)}
(
Y
=
y
)
{\displaystyle \displaystyle (Y=y)}
(
X
=
x
)
{\displaystyle (X=x)}
f
{\displaystyle \displaystyle f}
(
x
,
y
)
∈
X
×
Y
{\displaystyle (x,y)\in {\mathcal {X}}\times {\mathcal {Y}}}
H
(
Y
|
X
)
{\displaystyle \displaystyle H(Y|X)}
X
{\displaystyle X}
Y
{\displaystyle Y}
Let
H
(
Y
|
X
=
x
)
{\displaystyle \mathrm {H} (Y|X=x)}
entropy of the discrete random variable
Y
{\displaystyle Y}
X
{\displaystyle X}
x
{\displaystyle x}
X
{\displaystyle X}
Y
{\displaystyle Y}
X
{\displaystyle {\mathcal {X}}}
Y
{\displaystyle {\mathcal {Y}}}
Y
{\displaystyle Y}
probability mass function
p
Y
(
y
)
{\displaystyle p_{Y}{(y)}}
Y
{\displaystyle Y}
H
(
Y
)
:=
E
[
I
(
Y
)
]
{\displaystyle \mathrm {H} (Y):=\mathbb {E} [\operatorname {I} (Y)]}
H
(
Y
)
=
∑
y
∈
Y
P
r
(
Y
=
y
)
I
(
y
)
=
−
∑
y
∈
Y
p
Y
(
y
)
log
2
p
Y
(
y
)
,
{\displaystyle \mathrm {H} (Y)=\sum _{y\in {\mathcal {Y}}}{\mathrm {Pr} (Y=y)\,\mathrm {I} (y)}=-\sum _{y\in {\mathcal {Y}}}{p_{Y}(y)\log _{2}{p_{Y}(y)}},}
where
I
(
y
i
)
{\displaystyle \operatorname {I} (y_{i})}
information content of the outcome of
Y
{\displaystyle Y}
y
i
{\displaystyle y_{i}}
Y
{\displaystyle Y}
X
{\displaystyle X}
x
{\displaystyle x}
H
(
Y
|
X
=
x
)
=
−
∑
y
∈
Y
Pr
(
Y
=
y
|
X
=
x
)
log
2
Pr
(
Y
=
y
|
X
=
x
)
.
{\displaystyle \mathrm {H} (Y|X=x)=-\sum _{y\in {\mathcal {Y}}}{\Pr(Y=y|X=x)\log _{2}{\Pr(Y=y|X=x)}}.}
Note that
H
(
Y
|
X
)
{\displaystyle \mathrm {H} (Y|X)}
H
(
Y
|
X
=
x
)
{\displaystyle \mathrm {H} (Y|X=x)}
x
{\displaystyle x}
X
{\displaystyle X}
y
1
,
…
,
y
n
{\displaystyle y_{1},\dots ,y_{n}}
E
X
[
H
(
y
1
,
…
,
y
n
∣
X
=
x
)
]
{\displaystyle E_{X}[\mathrm {H} (y_{1},\dots ,y_{n}\mid X=x)]}
equivocation [ 2]
Given discrete random variables
X
{\displaystyle X}
X
{\displaystyle {\mathcal {X}}}
Y
{\displaystyle Y}
Y
{\displaystyle {\mathcal {Y}}}
Y
{\displaystyle Y}
X
{\displaystyle X}
H
(
Y
|
X
=
x
)
{\displaystyle \mathrm {H} (Y|X=x)}
x
{\displaystyle x}
p
(
x
)
{\displaystyle p(x)}
[ 3] : 15
H
(
Y
|
X
)
≡
∑
x
∈
X
p
(
x
)
H
(
Y
|
X
=
x
)
=
−
∑
x
∈
X
p
(
x
)
∑
y
∈
Y
p
(
y
|
x
)
log
2
p
(
y
|
x
)
=
−
∑
x
∈
X
,
y
∈
Y
p
(
x
)
p
(
y
|
x
)
log
2
p
(
y
|
x
)
=
−
∑
x
∈
X
,
y
∈
Y
p
(
x
,
y
)
log
2
p
(
x
,
y
)
p
(
x
)
.
{\displaystyle {\begin{aligned}\mathrm {H} (Y|X)\ &\equiv \sum _{x\in {\mathcal {X}}}\,p(x)\,\mathrm {H} (Y|X=x)\\&=-\sum _{x\in {\mathcal {X}}}p(x)\sum _{y\in {\mathcal {Y}}}\,p(y|x)\,\log _{2}\,p(y|x)\\&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}\,p(x)p(y|x)\,\log _{2}\,p(y|x)\\&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log _{2}{\frac {p(x,y)}{p(x)}}.\end{aligned}}}
Conditional entropy equals zero [ edit ]
H
(
Y
|
X
)
=
0
{\displaystyle \mathrm {H} (Y|X)=0}
Y
{\displaystyle Y}
X
{\displaystyle X}
Conditional entropy of independent random variables [ edit ] Conversely,
H
(
Y
|
X
)
=
H
(
Y
)
{\displaystyle \mathrm {H} (Y|X)=\mathrm {H} (Y)}
Y
{\displaystyle Y}
X
{\displaystyle X}
independent random variables .
Assume that the combined system determined by two random variables
X
{\displaystyle X}
Y
{\displaystyle Y}
joint entropy
H
(
X
,
Y
)
{\displaystyle \mathrm {H} (X,Y)}
H
(
X
,
Y
)
{\displaystyle \mathrm {H} (X,Y)}
X
{\displaystyle X}
H
(
X
)
{\displaystyle \mathrm {H} (X)}
X
{\displaystyle X}
H
(
X
,
Y
)
−
H
(
X
)
{\displaystyle \mathrm {H} (X,Y)-\mathrm {H} (X)}
H
(
Y
|
X
)
{\displaystyle \mathrm {H} (Y|X)}
chain rule of conditional entropy:
H
(
Y
|
X
)
=
H
(
X
,
Y
)
−
H
(
X
)
.
{\displaystyle \mathrm {H} (Y|X)\,=\,\mathrm {H} (X,Y)-\mathrm {H} (X).}
[ 3] : 17 The chain rule follows from the above definition of conditional entropy:
H
(
Y
|
X
)
=
∑
x
∈
X
,
y
∈
Y
p
(
x
,
y
)
log
(
p
(
x
)
p
(
x
,
y
)
)
=
∑
x
∈
X
,
y
∈
Y
p
(
x
,
y
)
(
log
(
p
(
x
)
)
−
log
(
p
(
x
,
y
)
)
)
=
−
∑
x
∈
X
,
y
∈
Y
p
(
x
,
y
)
log
(
p
(
x
,
y
)
)
+
∑
x
∈
X
,
y
∈
Y
p
(
x
,
y
)
log
(
p
(
x
)
)
=
H
(
X
,
Y
)
+
∑
x
∈
X
p
(
x
)
log
(
p
(
x
)
)
=
H
(
X
,
Y
)
−
H
(
X
)
.
{\displaystyle {\begin{aligned}\mathrm {H} (Y|X)&=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log \left({\frac {p(x)}{p(x,y)}}\right)\\[4pt]&=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)(\log(p(x))-\log(p(x,y)))\\[4pt]&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log(p(x,y))+\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}{p(x,y)\log(p(x))}\\[4pt]&=\mathrm {H} (X,Y)+\sum _{x\in {\mathcal {X}}}p(x)\log(p(x))\\[4pt]&=\mathrm {H} (X,Y)-\mathrm {H} (X).\end{aligned}}}
In general, a chain rule for multiple random variables holds:
H
(
X
1
,
X
2
,
…
,
X
n
)
=
∑
i
=
1
n
H
(
X
i
|
X
1
,
…
,
X
i
−
1
)
{\displaystyle \mathrm {H} (X_{1},X_{2},\ldots ,X_{n})=\sum _{i=1}^{n}\mathrm {H} (X_{i}|X_{1},\ldots ,X_{i-1})}
[ 3] : 22 It has a similar form to chain rule in probability theory, except that addition instead of multiplication is used.
Bayes' rule for conditional entropy states
H
(
Y
|
X
)
=
H
(
X
|
Y
)
−
H
(
X
)
+
H
(
Y
)
.
{\displaystyle \mathrm {H} (Y|X)\,=\,\mathrm {H} (X|Y)-\mathrm {H} (X)+\mathrm {H} (Y).}
Proof.
H
(
Y
|
X
)
=
H
(
X
,
Y
)
−
H
(
X
)
{\displaystyle \mathrm {H} (Y|X)=\mathrm {H} (X,Y)-\mathrm {H} (X)}
H
(
X
|
Y
)
=
H
(
Y
,
X
)
−
H
(
Y
)
{\displaystyle \mathrm {H} (X|Y)=\mathrm {H} (Y,X)-\mathrm {H} (Y)}
H
(
X
,
Y
)
=
H
(
Y
,
X
)
{\displaystyle \mathrm {H} (X,Y)=\mathrm {H} (Y,X)}
If
Y
{\displaystyle Y}
conditionally independent of
Z
{\displaystyle Z}
X
{\displaystyle X}
H
(
Y
|
X
,
Z
)
=
H
(
Y
|
X
)
.
{\displaystyle \mathrm {H} (Y|X,Z)\,=\,\mathrm {H} (Y|X).}
For any
X
{\displaystyle X}
Y
{\displaystyle Y}
H
(
Y
|
X
)
≤
H
(
Y
)
H
(
X
,
Y
)
=
H
(
X
|
Y
)
+
H
(
Y
|
X
)
+
I
(
X
;
Y
)
,
H
(
X
,
Y
)
=
H
(
X
)
+
H
(
Y
)
−
I
(
X
;
Y
)
,
I
(
X
;
Y
)
≤
H
(
X
)
,
{\displaystyle {\begin{aligned}\mathrm {H} (Y|X)&\leq \mathrm {H} (Y)\,\\\mathrm {H} (X,Y)&=\mathrm {H} (X|Y)+\mathrm {H} (Y|X)+\operatorname {I} (X;Y),\qquad \\\mathrm {H} (X,Y)&=\mathrm {H} (X)+\mathrm {H} (Y)-\operatorname {I} (X;Y),\,\\\operatorname {I} (X;Y)&\leq \mathrm {H} (X),\,\end{aligned}}}
where
I
(
X
;
Y
)
{\displaystyle \operatorname {I} (X;Y)}
mutual information between
X
{\displaystyle X}
Y
{\displaystyle Y}
For independent
X
{\displaystyle X}
Y
{\displaystyle Y}
H
(
Y
|
X
)
=
H
(
Y
)
{\displaystyle \mathrm {H} (Y|X)=\mathrm {H} (Y)}
H
(
X
|
Y
)
=
H
(
X
)
{\displaystyle \mathrm {H} (X|Y)=\mathrm {H} (X)\,}
Although the specific-conditional entropy
H
(
X
|
Y
=
y
)
{\displaystyle \mathrm {H} (X|Y=y)}
H
(
X
)
{\displaystyle \mathrm {H} (X)}
random variate
y
{\displaystyle y}
Y
{\displaystyle Y}
H
(
X
|
Y
)
{\displaystyle \mathrm {H} (X|Y)}
H
(
X
)
{\displaystyle \mathrm {H} (X)}
Conditional differential entropy [ edit ] The above definition is for discrete random variables. The continuous version of discrete conditional entropy is called conditional differential (or continuous) entropy . Let
X
{\displaystyle X}
Y
{\displaystyle Y}
joint probability density function
f
(
x
,
y
)
{\displaystyle f(x,y)}
h
(
X
|
Y
)
{\displaystyle h(X|Y)}
[ 3] : 249
h
(
X
|
Y
)
=
−
∫
X
,
Y
f
(
x
,
y
)
log
f
(
x
|
y
)
d
x
d
y
{\displaystyle h(X|Y)=-\int _{{\mathcal {X}},{\mathcal {Y}}}f(x,y)\log f(x|y)\,dxdy}
(Eq.2 )
In contrast to the conditional entropy for discrete random variables, the conditional differential entropy may be negative.
As in the discrete case there is a chain rule for differential entropy:
h
(
Y
|
X
)
=
h
(
X
,
Y
)
−
h
(
X
)
{\displaystyle h(Y|X)\,=\,h(X,Y)-h(X)}
[ 3] : 253 Notice however that this rule may not be true if the involved differential entropies do not exist or are infinite.
Joint differential entropy is also used in the definition of the mutual information between continuous random variables:
I
(
X
,
Y
)
=
h
(
X
)
−
h
(
X
|
Y
)
=
h
(
Y
)
−
h
(
Y
|
X
)
{\displaystyle \operatorname {I} (X,Y)=h(X)-h(X|Y)=h(Y)-h(Y|X)}
h
(
X
|
Y
)
≤
h
(
X
)
{\displaystyle h(X|Y)\leq h(X)}
X
{\displaystyle X}
Y
{\displaystyle Y}
[ 3] : 253
Relation to estimator error [ edit ] The conditional differential entropy yields a lower bound on the expected squared error of an estimator . For any random variable
X
{\displaystyle X}
Y
{\displaystyle Y}
X
^
{\displaystyle {\widehat {X}}}
[ 3] : 255
E
[
(
X
−
X
^
(
Y
)
)
2
]
≥
1
2
π
e
e
2
h
(
X
|
Y
)
{\displaystyle \mathbb {E} \left[{\bigl (}X-{\widehat {X}}{(Y)}{\bigr )}^{2}\right]\geq {\frac {1}{2\pi e}}e^{2h(X|Y)}}
This is related to the uncertainty principle from quantum mechanics .
Generalization to quantum theory [ edit ] In quantum information theory , the conditional entropy is generalized to the conditional quantum entropy . The latter can take negative values, unlike its classical counterpart.
















![{\displaystyle H(Y|X)=\mathbb {E} [f(X,Y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6e7cfdc7f8953ec5eed3ea5897b0b24223941d6b)











![{\displaystyle \mathrm {H} (Y):=\mathbb {E} [\operatorname {I} (Y)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f114631caeb95e508a74994486e35e972220b378)





![{\displaystyle E_{X}[\mathrm {H} (y_{1},\dots ,y_{n}\mid X=x)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c42f84b74f174cb4c172b6f91074f65dbd915e40)






![{\displaystyle {\begin{aligned}\mathrm {H} (Y|X)&=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log \left({\frac {p(x)}{p(x,y)}}\right)\\[4pt]&=\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)(\log(p(x))-\log(p(x,y)))\\[4pt]&=-\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p(x,y)\log(p(x,y))+\sum _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}{p(x,y)\log(p(x))}\\[4pt]&=\mathrm {H} (X,Y)+\sum _{x\in {\mathcal {X}}}p(x)\log(p(x))\\[4pt]&=\mathrm {H} (X,Y)-\mathrm {H} (X).\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/501bd3a915d2218c4464e1ea8cfefc3fba872320)


















![{\displaystyle \mathbb {E} \left[{\bigl (}X-{\widehat {X}}{(Y)}{\bigr )}^{2}\right]\geq {\frac {1}{2\pi e}}e^{2h(X|Y)}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab916a1ac9b14193bf90b79742772b686bb771c3)