Contrary (logic)
Appearance
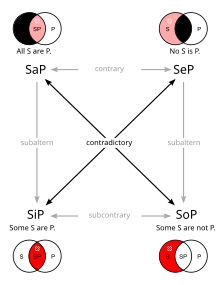
Contrary is the relationship between two propositions when they cannot both be true (although both may be false). Thus, we can make an immediate inference that if one is true, the other must be false.
The law holds for the A and E propositions of the Aristotelian square of opposition. For example, the A proposition 'every man is honest' and the E proposition 'no man is honest' cannot both be true at the same time, since no one can be honest and not honest at the same time. But both can be false, if some men are honest, and some men are not. For if some men are honest, the proposition 'no man is honest' is false. And if some men are not honest, the proposition 'every man is honest' is false also.
