Cycle graph (algebra)

In group theory, a sub-field of abstract algebra, a group cycle graph illustrates the various cycles of a group and is particularly useful in visualizing the structure of small finite groups. For groups with fewer than 16 elements, the cycle graph determines the group (up to isomorphism).

A cycle is the set of powers of a given group element a; where aⁿ, the n-th power of an element a, is defined as the product of a multiplied by itself n times. The element a is said to generate the cycle. In a finite group, some power of a must be the group identity, e; the lowest such power is the order of the cycle, the number of distinct elements in it. In a cycle graph, the cycle is represented as a series of polygons, with the vertices representing the group elements, and the connecting lines indicating that all elements in that polygon are members of the same cycle.

Cycles

Cycles can overlap, or they can have no element in common but the identity. The cycle graph displays each interesting cycle as a polygon.

If a generates a cycle of order 6 (or, more shortly, has order 6), then a⁶ = e. Then the set of powers of a², {a², a⁴, e} is a cycle, but this is really no new information. Similarly, a⁵ generates the same cycle as a itself.

So, we only need to consider the primitive cycles, those that are not subsets of another cycle. Each of these is generated by some primitive element, a. Take one point for each element of the original group. For each primitive element, connect e to a, a to a², ... a^n-1 to aⁿ, ... until you come back to e. The result is the cycle graph.

(Technically, the above description implies that if a² = e, so a has order 2 (is an involution), it's connected to e by two edges. It's conventional to only use one.)

Properties

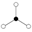
As an example of a group cycle graph, consider the dihedral group Dih₄. The multiplication table for this group is shown on the left, and the cycle graph is shown on the right with e specifying the identity element.

Cycle graph for dihedral group Dih₄.

o	e	b	a	a²	a³	ab	a²b	a³b
e	e	b	a	a²	a³	ab	a²b	a³b
b	b	e	a³b	a²b	ab	a³	a²	a
a	a	ab	a²	a³	e	a²b	a³b	b
a²	a²	a²b	a³	e	a	a³b	b	ab
a³	a³	a³b	e	a	a²	b	ab	a²b
ab	ab	a	b	a³b	a²b	e	a³	a²
a²b	a²b	a²	ab	b	a³b	a	e	a³
a³b	a³b	a³	a²b	ab	b	a²	a	e

Notice the cycle e, a, a², a³ . It can be seen from the multiplication table that successive powers of a in fact behave this way. The reverse case is also true. In other words: (a³)²=a² , (a³)³=a  and (a³)⁴=e . This behavior is true for any cycle in any group - a cycle may be traversed in either direction.

Cycle graph of the quaternion group Q₈.

Cycles that contain a non-prime number of elements implicitly have cycles that are not connected in the graph. For the group Dih₄ above, we might want to draw a line between a² and e  since (a²)²=e  but since a² is part of a larger cycle, this is not done.

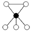
There can be ambiguity when two cycles share an element that is not the identity element. Consider for example, the simple quaternion group, whose cycle graph is shown on the right. Each of the elements in the middle row when multiplied by itself gives -1 (where 1 is the identity element). In this case we may use different colors to keep track of the cycles, although symmetry considerations will work as well.

As above, the 2-element cycles should be connected by two lines, but this is usually abbreviated by a single line.

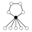
Two distinct groups may have cycle graphs that have the same structure, and can only be distinguished by the product table, or by labeling the elements in the graph in terms of the groups basic elements. The lowest order for which this problem can occur is order 16 in the case of Z₂ x Z₈ and the modular group, as shown below. (Note - the cycles with common elements are distinguished by symmetry in these graphs.)

Cycle graph of the order 16 group Z₂ x Z₈.

Cycle graph of the order 16 modular group.

The multiplication table of Z₂ x Z₈ is shown below:

0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
1	0	3	2	5	4	7	6	9	8	11	10	13	12	15	14
2	3	4	5	6	7	8	9	10	11	12	13	14	15	0	1
3	2	5	4	7	6	9	8	11	10	13	12	15	14	1	0
4	5	6	7	8	9	10	11	12	13	14	15	0	1	2	3
5	4	7	6	9	8	11	10	13	12	15	14	1	0	3	2
6	7	8	9	10	11	12	13	14	15	0	1	2	3	4	5
7	6	9	8	11	10	13	12	15	14	1	0	3	2	5	4
8	9	10	11	12	13	14	15	0	1	2	3	4	5	6	7
9	8	11	10	13	12	15	14	1	0	3	2	5	4	7	6
10	11	12	13	14	15	0	1	2	3	4	5	6	7	8	9
11	10	13	12	15	14	1	0	3	2	5	4	7	6	9	8
12	13	14	15	0	1	2	3	4	5	6	7	8	9	10	11
13	12	15	14	1	0	3	2	5	4	7	6	9	8	11	10
14	15	0	1	2	3	4	5	6	7	8	9	10	11	12	13
15	14	1	0	3	2	5	4	7	6	9	8	11	10	13	12

Other information derivable from cycle graphs

• The inverse of an element could be identified in the cycle graph. It is the element whose distance is the same from the opposite direction.

Graph characteristics of particular group families

Certain group types give typical graphs:

• Cyclic groups Z_n is a single cycle graphed simply as an n-sided polygon with the elements at the vertices.

Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8

• When n is a prime number, groups of the form (Z_n)^m will have (n^m-1)/(n-1) n-element cycles sharing the common identity element.

Z2²	Z2³	Z24	Z3²

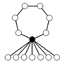
• Dihedral groups Dih_n consists of an n-element cycle and n 2-element cycles.

Dih1	Dih2	Dih3	Dih4	Dih5	Dih6	Dih7

• Symmetric groups - The symmetric group S_n contains, for any group of order n, a subgroup isomorphic to that group. Thus the cycle graph of every group of order n will be found as a subgraph of the cycle graph of S_n.

See also

• List of small groups
• Cayley graph

External links

• Cycle graph article on MathWorld

References

• Shanks, D. Solved and Unsolved Problems in Number Theory, 4th ed. New York: Chelsea, 1993.