Estimation of stature
Forensic estimation of stature is part of the identification process necessary when dismembered body parts are found. It is also possible to estimate the stature from bones.[2] Even measurements of body parts of body such as a finger can be used to estimate the stature.[3][4]
The principle behind this forensic anthropology technique is the fact that for a given combination of age, race, and gender there measurements of different body parts which have a relationship to the stature. This relationship between the measurements of body parts was known to sculptors and artists. In modern times, regression formulae are used to estimate stature from bones, fragments of bones or measurements of body parts.
History

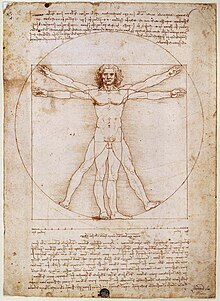
Vitruvius, who lived in the first century BC had put forth the proportions of human body in Book III, Chapter 1..
3. Just so the parts of Temples should correspond with each other, and with the whole. The navel is naturally placed in the centre of the human body, and, if in a man lying with his face upward, and his hands and feet extended, from his navel as the centre, a circle be described, it will touch his fingers and toes. It is not alone by a circle, that the human body is thus circumscribed, as may be seen by placing it within a square. For measuring from the feet to the crown of the head, and then across the arms fully extended, we find the latter measure equal to the former; so that lines at right angles to each other, enclosing the figure, will form a square.[5]
Leonardo da Vinci had based the proportions of the famous Vitruvian man on his writings.
Modern Research
In 1888 Rollet measured the stature and the lengths of the long bones of 50 male and 50 female French cadavers ranging in age from 24 to 99 years, and presented tables for stature estimation. He determined the average length of the long bones of those who presented the same stature.[6]
Manouvrier (1892 and 1893) found that due to the effect of old age the length of the trunk was 3 cm less than the maximum stature. He excluded those aged above 60 years from his sample and derived tables of average stature corresponding to given long bone lengths. Manouvrier determined the average stature of those individuals who presented the same lengths for a given long bone.[6]
Karl Pearson (1899) applied stature regression formulae utilizing all of Rollet’s cases.[6]
In 1929 Stevenson accumulated data on Northern Chinese male cadavers using the same methods as those used by Rollet. He found that the stature regression formulae he derived could not be used to determine the stature of french population and Pearsn's formulae derived for the french could not be used in his sample.[6]
Breitinger (1937) measured the distance between certain anatomical prominence in a sample of 2400 German males of whom 1400 were participants in an athletic meet in Munich in 1923. 1000 members of the sample were students in 1925-26. The average age of the group was about 26 years.[6]
Telkka (1950) studied 154 Finnish cadavers, 115 males and 39 females. The average age of the males in the sample was 42.3 years and of the females 50.4 years. The stature of the cadavers was measured on the “prostrate” corpse and the bones were measured after maceration and drying.[6]
Dupertuis and Hadden (1951) derived regression equations for calculation of stature from a sample of 100 male whites, 100 female whites, 100 male Negroes and 100 female Negroes.[7]
Trotter and Gleser (1952) compared the stature of servicemen (male American Whites and Negroes) in their military records and the length of bones of the skeletal remains measured at the time of repatriation of their skeletal remains.[6] They later analyzed same data obtained after the Korean War. This time, regression equations for Whites, Negroes, Mongoloids, Mexicans and Puerto Ricans were derived.[8]
Calculation of Stature from the Length of Long Bones
Many different equations are in use for estimation of stature from the length of long bones.
Karl Pearson
He derived reconstruction formulae for living stature from dry bones. The probable error is given in parentheses.[9]
| Bone | Male Whites | Female Whites |
|---|---|---|
| Femur | 81.306 + 1.880 F (±0.3047) | 72.844 + 1.945 F (±0.3058) |
| Tibia | 78.664 + 2.376 T (±0.3275) | 74.774 + 2.352 T (±0.3146) |
| Humerus | 70.641 + 2.894 H (±0.3056) | 71.475 + 2.754 H (±0.3284) |
| Radius | 85.925 + 3.271 R (±0.3728) | 81.224 + 3.343 R (±0.3816) |
| Femur & Tibia | 71.272 + 1.159 (F + T) (±0.2835) | 69.154 + 1.126 (F + T) (±0.2898) |
| Humerus & Radius | 66.855 + 1.730 (H + R) (±0.3139) | 69.911 + 1.628 (H + R) (±0.3380) |
| Femur & Tibia | 71.443 + 1.220 F + 1.080 T (±0.2845) | 69.561 + 1.117 F + 1.125 T (±0.2922) |
| Humerus & Radius | 69.788 + 2.769 H + 0.195 R (±0.3054) | 70.542 + 2.582 H + 0.281 R (±0.3279) |
| Femur & Humerus | 68.397 + 1.030 F + 1.557 H (±0.2750) | 67.435 + 1.339 F + 1.037 H (±0.2971) |
| Femur, Tibia, Humerus & Radius | 67.049 + 0.913 F + 0.600 T + 1.225 H - 0.187 R (±0.2748) | 67.469 + 0.782 F + 1.120 T + 1.059 H - 0.711 R (±0.2836) |
Trotter and Gleser
The regression equations to calculate stature in centimeters for male servicemen belonging to different races derived by Trotter and Gleser. Probable errors are given within parentheses.[8]
| Bone | Whites | Negroes | Mongoloids | Mexicans | Puerto Ricans |
|---|---|---|---|---|---|
| Rt Humerus | 2.88 HR + 77.70 (±4.61) | 2.88 HR + 75.52 (±4.26) | 2.69 HR + 82.80 (±4.32) | 3.01 HR + 70.40 (±4.29) | 2.45 HR + 88.45 (±3.96) |
| Lt Humerus | 2.89 HL + 77.47 (±4.54) | 2.89 HL + 75.10 (±4.21) | 2.68 HL + 83.27 (±4.18) | 2.82 HL + 77.32 (±4.20) | 2.79 HL + 77.18 (±3.63) |
| Rt Radius | 3.77 RR + 79.13 (±4.66) | 3.28 RR + 86.22 (±4.65) | 3.58 RR + 80.71 (±4.64) | 3.79 RR + 74.59 (±4.09) | 3.24 RR + 86.76 (±4.00) |
| Lt Radius | 3.73 RL + 80.62 (±4.59) | 3.36 RL + 84.63 (±4.50) | 3.51 RL + 83.40 (±4.55) | 3.30 RL + 87.05 (±4.00) | 3.33 RL + 85.20 (±3.80) |
| Rt Ulna | 3.59 UR + 76.95 (±4.71) | 3.13 UR + 84.42 (±4.73) | 3.50 UR + 76.07 (±4.84) | 3.82 UR + 67.67 (±3.92) | 3.11 UR + 84.60 (±4.02) |
| Lt Ulna | 3.64 UL + 76.14 (±4.57) | 3.28 UL + 80.85 (±4.76) | 3.46 UL + 78.84 (±4.49) | 3.30 UL + 81.46 (±4.18) | 3.48 UL + 75.59 (±3.81) |
| Rt Femur | 2.25 FR + 68.40 (±4.04) | 2.07 FR + 73.78 (±3.83) | 2.12 FR + 74.03 (±3.92) | 2.41 FR + 59.84 (±3.10) | 2.09 FR + 72.86 (±3.18) |
| Lt Femur | 2.30 FL + 65.82 (±3.97) | 2.14 FL + 70.19 (±3.99) | 2.18 FL + 71.11 (±3.67) | 2.47 FL + 57.51 (±2.88) | 2.11 FL + 72.36 (±3.19) |
| Rt Tibia | 2.40 TR + 82.24 (±3.97) | 2.20 TR + 84.90 (±3.88) | 2.42 TR + 80.36 (±3.26) | 2.29 TR + 83.46 (±3.59) | 2.05 TR + 90.49 (±3.61) |
| Lt Tibia | 2.43 TL + 80.98 (±3.95) | 2.18 TL + 85.82 (±4.04) | 2.36 TL + 82.54 (±3.28) | 2.42 TL + 78.13 (±3.88) | 1.95 TL + 94.57 (±3.80) |
| Rt Fibula | 2.57 FR + 76.13 (±3.86) | 2.38 FR + 78.48 (±3.96) | 2.39 FR + 81.10 (±3.20) | 2.56 FR + 73.30 (±3.32) | 2.09 FR + 89.88 (±3.48) |
| Lt Fibula | 2.59 FL + 75.37 (±3.83) | 2.29 FL + 82.02 (±4.08) | 2.40 FL + 80.38 (±3.28) | 2.44 FL + 77.58 (±3.72) | 2.16 FL + 87.27 (±3.79) |
Dupertuis and Hadden
The regression equations derived by Dupertuis and Hadden for Whites and Blacks to estimate the stature in centimeters from individual long bones and different combinations are given below. Probable errors are given within parentheses.[7]
| Bone | Male Whites | Female Whites | Male Negroes | Female Negroes |
|---|---|---|---|---|
| Femur | 77.048 + 2.116 F (±0.2308) | 62.872 + 2.322 F (±0.2256) | 55.021 + 2.540 F (±0.2819) | 54.235 + 2.498 F (±0.2419) |
| Tibia | 92.766 + 2.178 T (±0.2436) | 71.652 + 2.635 T (±0.2433) | 72.123 + 2.614 T (±0.2983) | 72.391 + 2.521 T (±0.2867) |
| Humerus | 98.341 + 2.270 H (±0.3094) | 56.287 + 3.448 H (±0.2762) | 50.263 + 3.709 H (±0.2762) | 69.978 + 3.035 H (±0.3189) |
| Radius | 88.881 + 3.449 R (±0.2907) | 68.238 + 4.248 R (±0.2963) | 69.168 + 4.040 R (±0.3522) | 74.906 + 3.761 R (±0.3277) |
| Femur & Tibia | 84.898 + 1.072 (F + T) (±0.2508) | 57.872 + 1.354 (F + T) (±0.2016) | 52.702 + 1.411 (F + T) (±0.2485) | 70.584 + 1.165 (F + T) (±0.2953) |
| Humerus & Radius | 87.543 + 1.492 (H + R) (±0.2889) | 42.386 + 2.280 (H + R) (±0.2134) | 57.601 + 1.962 (H + R) (±0.3564) | 61.982 + 1.866 (H + R) (±0.2926) |
| Femur & Tibia | 76.201 + 1.330 F + 0.991 T (±0.2173) | 60.377 + 1.472 F + 1.133 T (±0.2063) | 54.438 + 1.615 F + 1.123 T (±0.2559) | 52.989 + 2.112 F + 0.501 T (±0.2397) |
| Humerus & Radius | 82.831 + 0.907 H + 2.474 R (±0.2835) | 53.187 + 2.213 H + 1.877 R (±0.2632) | 48.275 + 2.182 H + 2.032 R (±0.3251) | 62.402 + 1.906 H + 1.796 R (±0.3082) |
| Femur & Humerus | 78.261 + 2.129 F - 0.055 H (±0.2328) | 55.179 + 1.835 F + 0.935 H (±0.1827) | 48.802 + 2.175 F + 0.696 H (±0.2749) | 55.103 + 2.517 F + 0.033 H (±0.2380) |
| Tibia & Radius | 88.581 + 1.945 T + 0.524 R (±0.2385) | 64.702 + 2.089 T + 1.169 R (±0.2328) | 67.964 + 2.260 T + 0.689 R (±0.2964) | 66.005 + 2.076 T + 0.952 R (±0.2832) |
| Femur, Tibia, Humerus & Radius | 52.618 + 1.512 F + 0.927 T - 0.490 H + 1.386 R (±0.1582) | 56.660 + 1.267 F + 0.992 T + 0.449 H + 0.164 R (±0.2068) | 53.873 + 1.637 F + 1.101 T + 0.084 H - 0.093 R (±0.2626) | 53.342 + 2.201 F + 0.359 T - 0.663 H + 0.930 R (±0.2365) |
Calculation of Stature from the measurement of Body Parts
Various studies have been undertaken into methods to device the estimation of stature from foot prints, measurement of severed body parts etc.
References
- ^ Bogin, Barry; Inês Varela-Silva, Maria (2010). "Leg Length, Body Proportion, and Health: A Review with a Note on Beauty". Int. J. Environ. Res. Public Health. 7 (3). doi:10.3390/ijerph7031047. Retrieved 18 October 2017.
{{cite journal}}: CS1 maint: unflagged free DOI (link) - ^ Kamal, Renu; Yadav, Praveen Kumar (December 2016). "Estimation of stature from different anthropometric measurements in Kori population of North India". Egyptian Journal of Forensic Sciences. 6 (4): 468–477. doi:10.1016/j.ejfs.2016.12.001. Retrieved 17 October 2017.
- ^ Hussain, Sheik Shakeer S; Balachandran, Ajay (August 2017). "Determination of Stature from the Length of Middle Finger - An Autopsy Study". JEMDS. 6 (70): 5009–12. doi:10.14260/Jemds/2017/1088. Retrieved 17 October 2017.
- ^ Hussein, Sheik Shakeer S; Balachandran, Ajay (September 2017). "The Relationship Between Foot Index and Stature in Kerala Population - A Descriptive Study". JEMDS. 6 (73): 5221–24. doi:10.14260/Jemds/2017/1134. Retrieved 17 October 2017.
- ^ "LacusCurtius • Vitruvius on Architecture — Book III". penelope.uchicago.edu. Retrieved 20 June 2017.
- ^ a b c d e f g Trotter, M; Gleser, GC (Dec 1952). "Estimation of stature from long bones of American Whites and Negroes". Am. J. Phys. Anthropol. 10 (4): 463–514. PMID 13007782.
- ^ a b Dupertuis, CW; Hadden, JA Jr (March 1951). "On the reconstruction of stature from long bones". Am. J. Phys. Anthropol. 9 (1): 15–53. doi:10.1002/ajpa.1330090104. PMID 14819267.
- ^ a b Trotter, M; Gleser, GC (March 1958). "A re-evaluation of estimation of stature based on measurements of stature taken during life and of long bones after death". Am. J. Phys. Anthropol. 16 (1): 79–123. PMID 13571400. Retrieved 21 October 2017.
- ^ Pearson, K (January 1899). "IV. Mathematical contributions to the theory of evolution.—V. On the reconstruction of the stature of prehistoric races". Phil. Trans. Royal Soc. A (193): 169–244. doi:10.1098/rsta.1899.0004. Retrieved 27 October 2017.
