File:Lemoine Hexagon.svg
Page contents not supported in other languages.
Tools
Actions
General
In other projects
Appearance

Size of this PNG preview of this SVG file: 600 × 600 pixels. Other resolutions: 240 × 240 pixels | 480 × 480 pixels | 768 × 768 pixels | 1,024 × 1,024 pixels | 2,048 × 2,048 pixels.
Original file (SVG file, nominally 800 × 800 pixels, file size: 2 KB)
| This is a file from the Wikimedia Commons. Information from its description page there is shown below. Commons is a freely licensed media file repository. You can help. |
Summary
| DescriptionLemoine Hexagon.svg |
English: Lemoine Hexagon and its construction |
| Date | |
| Source | Own work |
| Author | Claudio Rocchini |
Source Code
#include <stdio.h>
#include <math.h>
class point
{
public:
double x,y;
point() {}
point( double nx, double ny ) : x(nx),y(ny) {}
point operator+ ( const point & p ) const { return point(x+p.x,y+p.y); }
point operator- ( const point & p ) const { return point(x-p.x,y-p.y); }
point operator* ( const double s ) const { return point(x*s,y*s); }
double operator* ( const point & p ) const { return x*p.x+p.y*y; } // dot product
double operator^ ( const point & p ) const { return x*p.y-p.x*y; } // cross product
double angle() const { return atan2(y,x); }
point& at_angle( double a ) { x = cos(a); y = sin(a); return *this; }
point perp() const { return point(y,-x); }
double norm () const { return sqrt(x*x+y*y); }
point& normalize() { double n = norm(); if(n!=0) { x/=n; y/=n; } return *this; }
};
class line
{
public:
point orig;
point dire;
line() {}
line( const point & no, const point & nd ) : orig(no),dire(nd) {}
point param( double t ) const { return orig+dire*t; }
point intersect( const line & l ) { return param( (l.dire^(orig-l.orig))/(dire^l.dire) ); }
};
void main()
{
const double SX = 800; const double SY = 800;
const double S = 700; const double Q = 75;
const int N = 3;
int i;
point tri[N] = { point(80,50) ,point(680,750), point(165,715) };
line median [N];
line bisector [N];
line symmedian[N];
point inter[N][2];
for(i=0;i<N;++i) {
median[i].orig = tri[i];
median[i].dire = ((tri[(i+1)%N]+tri[(i+2)%N])*0.5 - tri[i]).normalize();
bisector[i].orig = tri[i];
bisector[i].dire = (tri[(i+1)%N]-tri[i]).normalize() + (tri[(i+2)%N]-tri[i]).normalize();
bisector[i].dire.normalize();
symmedian[i].orig = tri[i];
symmedian[i].dire.at_angle( bisector[i].dire.angle()*2 - median[i].dire.angle() );
}
point symmedian_p = symmedian[0].intersect(symmedian[1]);
for(i=0;i<N;++i) {
line pa(symmedian_p, (tri[(i+2)%N]-tri[(i+1)%N]).normalize() );
for(int j=0;j<2;++j) {
line la(tri[i], (tri[(i+1+j)%N]-tri[i]).normalize() );
inter[i][j] = pa.intersect(la);
}
}
line l1( (inter[0][0]+inter[0][1])*0.5, (inter[0][0]-inter[0][1]).perp().normalize() );
line l2( (inter[1][0]+inter[1][1])*0.5, (inter[1][0]-inter[1][1]).perp().normalize() );
point first_lem_c = l1.intersect(l2);
double first_lem_r = (first_lem_c-inter[0][0]).norm();
FILE * fp = fopen("c:\\temp\\Lemoine_Hexagon.svg","w");
fprintf(fp,
"<?xml version=\"1.0\" encoding=\"UTF-8\" standalone=\"no\"?>\n"
"<svg\n"
"xmlns:svg=\"http://www.w3.org/2000/svg\"\n"
"xmlns=\"http://www.w3.org/2000/svg\"\n"
"version=\"1.0\"\n"
"width=\"%g\"\n"
"height=\"%g\"\n"
"id=\"Lemoine_Hexagon\">\n"
,SX,SY
);
fprintf(fp,"<g style=\"stroke:#0000C0;stroke-width:1;stroke-opacity:1;stroke-dasharray:6,4;fill:none\">\n");
for(i=0;i<N;++i)
fprintf(fp,
"<line x1=\"%5.1lf\" y1=\"%5.1lf\" x2=\"%5.1lf\" y2=\"%5.1lf\"/>\n"
,median[i].orig.x,median[i].orig.y
,(median[i].orig+median[i].dire*S).x,(median[i].orig+median[i].dire*S).y
);
fprintf(fp,"</g>\n");
fprintf(fp,"<g style=\"stroke:#00C000;stroke-width:1;stroke-opacity:1;stroke-dasharray:6,4;fill:none\">\n");
for(i=0;i<N;++i)
fprintf(fp,
"<line x1=\"%5.1lf\" y1=\"%5.1lf\" x2=\"%5.1lf\" y2=\"%5.1lf\"/>\n"
,bisector[i].orig.x,bisector[i].orig.y
,(bisector[i].orig+bisector[i].dire*S).x,(bisector[i].orig+bisector[i].dire*S).y
);
fprintf(fp,"</g>\n");
fprintf(fp,"<g style=\"stroke:#C00000;stroke-width:1;stroke-opacity:1;stroke-dasharray:6,4;fill:none\">\n");
for(i=0;i<N;++i)
fprintf(fp,
"<line x1=\"%5.1lf\" y1=\"%5.1lf\" x2=\"%5.1lf\" y2=\"%5.1lf\"/>\n"
,symmedian[i].orig.x,symmedian[i].orig.y
,(symmedian[i].orig+symmedian[i].dire*S).x,(symmedian[i].orig+symmedian[i].dire*S).y
);
fprintf(fp,"</g>\n");
fprintf(fp,"<g style=\"stroke:#C0C0C0;stroke-width:1;stroke-opacity:1;stroke-dasharray:6,4;fill:none\">\n");
for(i=0;i<N;++i) {
point d = (inter[i][1] - inter[i][0]).normalize();
point p1 = inter[i][0] - d*Q; point p2 = inter[i][1] + d*Q;
fprintf(fp,
"<line x1=\"%5.1lf\" y1=\"%5.1lf\" x2=\"%5.1lf\" y2=\"%5.1lf\"/>\n"
,p1.x, p1.y, p2.x, p2.y
);
}
fprintf(fp,"</g>\n");
fprintf(fp,"<g style=\"stroke:#00C0C0;stroke-width:1;stroke-opacity:1;fill:none\">\n");
fprintf(fp,"<circle cx=\"%5.1lf\" cy=\"%5.1lf\" r=\"%5.1lf\"/>\n"
,first_lem_c.x, first_lem_c.y
,first_lem_r
);
fprintf(fp,"</g>\n");
fprintf(fp,"<g style=\"stroke:#C000C0;stroke-width:2;stroke-opacity:1;fill:none\">\n");
fprintf(fp,"<path d=\"");
for(i=0;i<3;++i){
if(i==0) fprintf(fp,"M ");
else fprintf(fp,"L ");
fprintf(fp,"%5.1lf,%5.1lf ",tri[i].x,tri[i].y);
}
fprintf(fp,"z\"/>\n");
fprintf(fp,"</g>\n");
fprintf(fp,"<g style=\"stroke:#000000;stroke-width:2;stroke-opacity:1;fill:#C0C000;fill-opacity:0.5\">\n");
fprintf(fp,"<path d=\"");
for(i=0;i<3;++i) {
for(int j=0;j<2;++j) {
if(i==0 && j==0) fprintf(fp,"M ");
else fprintf(fp,"L ");
fprintf(fp,"%5.1lf,%5.1lf ",inter[i][j]);
}
}
fprintf(fp,"z\"/>\n");
fprintf(fp,"</g>\n");
fprintf(fp,"<g style=\"stroke:none;fill:#000000\">\n");
fprintf(fp,"<circle cx=\"%5.1lf\" cy=\"%5.1lf\" r=\"%5.1lf\"/>\n"
,symmedian_p.x, symmedian_p.y
,6.0
);
for(i=0;i<N;++i) for(int j=0;j<2;++j)
fprintf(fp,"<circle cx=\"%5.1lf\" cy=\"%5.1lf\" r=\"%5.1lf\"/>\n"
,inter[i][j].x, inter[i][j].y
,6.0
);
fprintf(fp,"</g>\n");
fprintf(fp,"</svg>\n");
fclose(fp);
}
Licensing
Claudio Rocchini, the copyright holder of this work, hereby publishes it under the following licenses:

|
Permission is granted to copy, distribute and/or modify this document under the terms of the GNU Free Documentation License, Version 1.2 or any later version published by the Free Software Foundation; with no Invariant Sections, no Front-Cover Texts, and no Back-Cover Texts. A copy of the license is included in the section entitled GNU Free Documentation License.http://www.gnu.org/copyleft/fdl.htmlGFDLGNU Free Documentation Licensetruetrue |
This file is licensed under the Creative Commons Attribution 3.0 Unported license.
Attribution: Claudio Rocchini
- You are free:
- to share – to copy, distribute and transmit the work
- to remix – to adapt the work
- Under the following conditions:
- attribution – You must give appropriate credit, provide a link to the license, and indicate if changes were made. You may do so in any reasonable manner, but not in any way that suggests the licensor endorses you or your use.
You may select the license of your choice.
Captions
Add a one-line explanation of what this file represents
Items portrayed in this file
depicts
some value
9 July 2008
File history
Click on a date/time to view the file as it appeared at that time.
| Date/Time | Thumbnail | Dimensions | User | Comment | |
|---|---|---|---|---|---|
| current | 08:32, 9 July 2008 | 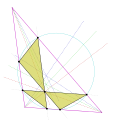 | 800 × 800 (2 KB) | Rocchini | {{Information |Description={{en|1=Lemoine Hexagon and its construction}} |Source=Opera creata dall'uploader (own work by uploader) |Author=Claudio Rocchini |Date=2008-07-09 |Permission= |other_versions= }} {{ImageUpload|full}} |
File usage
The following 3 pages use this file:
Global file usage
The following other wikis use this file:
- Usage on en.wiktionary.org
- Usage on fr.wikipedia.org
- Usage on ja.wikipedia.org
- Usage on ru.wikipedia.org
Retrieved from "https://en.wikipedia.org/wiki/File:Lemoine_Hexagon.svg"
